8 Advanced Propositional Logic

Introduction

Our basic 8 inference rules allow us to demonstrate the validity of many arguments. However, they do not allow us to do so for all formally valid arguments. There is only so much we can do within our system thus far, so we will need additional rules that open up strategic possibilities.

Replacement rules are also referred to as “equivalence rules,” because they express logically equivalent statement forms. By using equivalence rules, we are simply exchanging one statement form for another, logically equivalent, statement form. We are not inferring something new. We are simply “restating” what was already established.

You might wonder why we would do this. The answer is found in everyday life.

If you have ever stood in front of a vending machine with a $20 bill in your hand, you know the frustration of having what you need but having it in a difficult form. What to do? Of course, you go ask someone to trade you for a more useful version of your money. You will be happy to get a $10 bill, a $5 bill, and five singles. You haven’t made money, you haven’t lost money. You got the exact same value.

The same is true of our equivalence rules. We don’t lose or gain value—the truth value of our statements must stay the same to make it a fair trade.

Now that I have my $20 of value in a new form, I have greater ability to do things I want to do with it. Here again we see the emphasis on the goal. We use the replacement rules wisely when we know what we want. Knowing our goals makes their use sensible—it would be very odd indeed to walk around randomly asking people to break your $20 bill.

So, nothing has fundamentally changed with our method. We still start with our goals. We still use the reverse method of generating a linear problem-solving strategy to achieve those goals. The only difference is that now we have many more strategic opportunities. After all, when we identify our goal and we identify our resources, we are identifying a type of statement. Now, those types (i.e., those $20 bills) can morph into different types of statements. This greatly expands the range of moves we can make. We gain tremendous flexibility in how we solve a proof as well as the ability to solve proofs that were previously closed off from us. This is very good. However, this also adds a great deal of complexity to our proofs. Now the really fun proofs can begin!

We will look at 10 replacement rules overall, but we’ll do so in two sets. The first set is a good introduction to using replacement rules. The patterns there are not too difficult to learn. The second set is a bit more complicated.

We will also introduce a new symbol:

∷

This symbol expresses equivalency (think of it like a mathematical = sign). The four dots are different from the three dots that expressed an inference. Three dots are directional. You can only infer the conclusion on the basis of the previous statement(s). Consider:

The rule Simp tells us that knowing □ ∙△ allows us to infer that □ is true. However, knowing that □ is true by itself tells you nothing about the truth of the whole conjunction □ ∙△. You cannot infer that statement on the basis of the conclusion.

With the ∷ things are different. You can assert that one side of the ∷ is true on the basis of what is on the other side. Four dots are bidirectional.

First 5 Replacement Rules

Double Negation (DN)

Double negation is a straightforward rule, and as such is a good place to start. The form of the rule is as follows:

□ ∷ ~ ~ □

We see that this rule applies to any statement of any form. Any □ can be replaced with its equivalent version ~ ~ □. Your English teacher may not approve, but in our symbolic language this is a perfectly acceptable statement form. In some cases, this is exactly the form that is required to satisfy the use of a different rule (think: an instance of modus ponens in which the antecedent of the conditional is something like ~ ~ G, and you only have a G to work with).

DN is such a simple rule that it is also useful in illustrating some unique features and requirements of the replacement rules. These are:

1. You can use them anywhere in a statement that the patterns apply (i.e., their use is not restricted to the main connective)
2. You can only use them one at a time
3. Replacement rules always only reference one line
4. You can use them on the same statement in a different part of the statement (so long as the pattern they express applies)

So let’s look at a simple example. Consider the following:

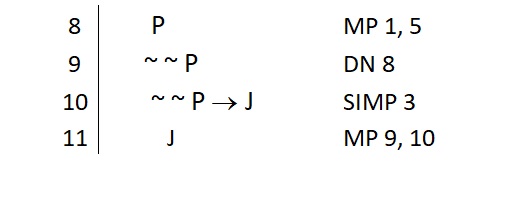
I used DN to change line 8 into the ~ ~ P that I needed to satisfy the conditional on line 10. However, I didn’t need to use DN in this specific way. Eventually I want to get the J out of that conditional, but I could instead have done this:

Notice that in this use of DN, I only applied it to the antecedent of the conditional. Because the ∷ of all replacement rules is bidirectional, I can use DN to take away a ~ ~ if I want to do so. This “cleans up” the conditional and changes what is needed to deliver the J that I want. Either use of DN is permissible, and the decision in cases like this comes down to personal preference.

Keep in mind that I am not restricted to using DN on atomic statements. We can use it on any □ we elect, even if it is a compound statement. For example:

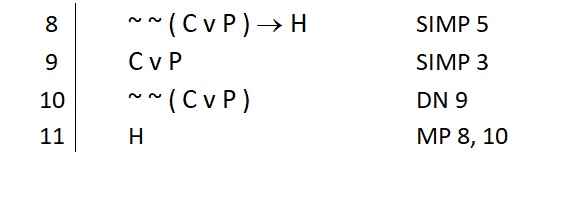
We can use DN on an entire line or on just part of a line. Put differently, I can use DN on the main connective of a line or on just a component of the line.

The one thing we cannot do with any replacement rules is use a rule more than once on a given line or use it with other rules on the same line. If I want to make multiple changes, I need to do so in two different steps. Like this:

Note the red emphasis placed on each application of DN to illustrate each single application of our replacement rule. Also note that in my second application of DN (on line 11) I applied the rule to line 10. I did not apply DN “again” to line 9. This is important because any time I apply a replacement rule to a component of a given line, the other parts of that line do not change. When we look at line 11 we see that all other aspects of line 10 are still there—only the single use of DN has changed line 10 into line 11.

A Word of Warning:

You can see how flexible the replacement rules can be…and how much trouble they can get you in if not used with purpose. In theory, you can make an infinite number of moves with just this one replacement rule. If you are not careful, you will quickly go down a deep rabbit hole of desperate replacements…hoping something wonderful happens.^[1]

Commutation (Com)

The rule of commutation applies to And statements and Or statements. When we look closely at the basic conditions of truth for these statements in a truth table, we see that the order of the component statements has no impact on their truth. So this rule allows us to make use of that knowledge. The form of the rule is as follows:

□ ∙ △  ∷    △ ∙ □

□ v △   ∷    △ v □

Commutation allows us to swap the order of the conjuncts or disjuncts on any subsequent line of a proof. Here’s an example:

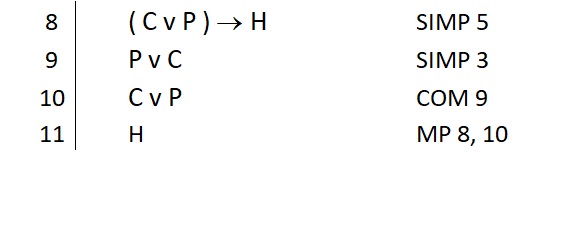
You might think this is a trivial rule, but it has great use, especially when combined with the following rule.

Association (As)

The rule of association is used like a rule to signal friendship. Close friends are bound together by ( ) in a large compound. Consider this statement:

S ∙ ( N ∙ K )

Who are the besties?

And who is left out in the cold?

Clearly we see that ( N ∙ K ) are best friends and S is kind of the third wheel. But sometimes we can change that. The form of association is as follows:

□ ∙ ( △ ∙ ○ )        ∷        ( □ ∙ △ ) ∙ ○

□ v ( △ v ○ )         ∷       ( □ v △ ) v ○

Notice that the order of the components does not change. All we are doing is changing the grouping of the statements. If we want to change the order of the component statements, then we have the rule of commutation for that. A combination of association and commutation gives us great control over how such statements can look. We will use these two rules together often.

A Word of Warning: We can only do this when we have a string of ∙s or a string of vs. This rule does not work with any other type of statement.

DeMorgan’s Law (DeM)

This is one of the most useful replacement rules we have in our system. DeMorgan’s Law will become a great personal friend, as it will get you out of trouble many times. The rule itself expresses what the denial of an And (or an Or) statement really means. The form looks like this:

~ ( □ ∙ △ )       ∷       ~ □ v ~ △

~ ( □ v △ )       ∷       ~ □ ∙ ~ △

The savvy student will notice two things. First, we are not simply moving the ~ inside the ( ) when we use this rule. Doing this does not produce logically equivalent statements. When we move the ~ inside the ( ), we must also change the operator there. The “∙” becomes a “v” and the “v” becomes a “∙”.

The savvy student also notices something else. Having the denial of an Or statement now becomes very fruitful (e.g., when you have one given to you in the premises). We can transform that into an And statement, and Simp makes it easy to grab whichever side we want.

Additionally, we might be frustrated if we need the negation of an And statement (e.g., when you need that to pull off a modus tollens or a disjunctive syllogism). At least, we are only frustrated until we realize that all we really need is the negation of either side. With a ~ □ or a ~ △ on a line, we can use Add to build the rest and flip back with DeMorgan’s into the denial we wanted all along.

Identifying these patterns is key:

“Negation of an And statement”

“Negation of an Or statement”

When those phrases pass through your mind, you will have a good chance of remembering this rule and the power it has to get you to your next move.

Also note that as with all replacement rules, we can use this anywhere within a statement, on the main connective or on just a component of the statement. For example:

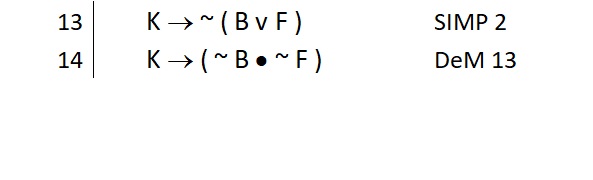
Contraposition (Cont)

The rule of contraposition applies to conditional statements. The form looks like this:

□ → △       ∷       ~ △ → ~ □

The savvy student may recognize the relationship that this rule expresses. Ask yourself: What does this remind you of when you read it from left to right?

Go ahead, take another look…

We’ll wait…

If you said, “Hey, it looks kind of like modus tollens,” you are right. Contraposition expresses the same relationship found in all conditionals; it just doesn’t allow us to infer that ~ □ is actually true. Instead, the rule tells us what to expect if the necessary condition is false (i.e., the sufficient condition could not have been met).

All this rule allows us to do is swap the positions (thus, contra–position) of the antecedent and consequent. Of course, we cannot do this cleanly. If we just swapped positions the way we do with commutation, we would get a false equivalency. Swapping positions in a conditional requires us to deny each component in the new conditional.

This rule is very useful for setting up a hypothetical syllogism such as this:

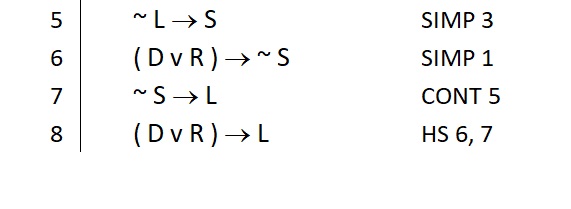
This rule is also a favorite of students who (for their own personal reasons) just don’t like to use modus tollens. Now you don’t have to put up with MT if you don’t want to use that rule. You can always convert a strategy that would require the use of MT into a strategy that uses the more comfortable MP rule.

Of course, what you need to pay off the new conditional is exactly the same as what you would need to pull off the MT (note the red emphasis placed on ~ H to point this out). The proof does not become easier in this regard, but at least you’ll feel better about it. That’s something.

First 5 Replacement Rules Problem Set

First 5 Replacement Rules Problem Set [PDF, 41 KB]

Second 5 Replacement Rules

Redundancy (Re)

We claimed that the second set of replacement rules would involve more complex patterns. This is mostly true—except for this one. This is likely the most banal rule we have, but it serves a useful purpose from time to time. Here is the form:

□       ∷       □ v □

□       ∷       □ ∙ □

Note that this rule applies to any statement, i.e., any □. The use of the rule comes into its own when we find odd situations where we may be able to produce an Or statement like □ v □, but cannot produce the □ on its own (think: being forced into a constructive dilemma because you couldn’t pay off either conditional to use MP).

Redundancy allows us to fold this into the □ we wanted all along.

Distribution (Dist)

The rule of distribution has two applications, one for peculiar conjunctions and one for peculiar disjunctions. The form looks like this:

□ ∙ ( △ v ○ )       ∷       ( □ ∙ △ ) v ( □ ∙ ○ )

□ v ( △ ∙ ○ )       ∷       ( □ v △ ) ∙ ( □ v ○ )

Note that what we see on the left side of the four dots are the And and Or statements with unique features. The And statement is peculiar because it contains a conjunct which is itself an Or statement.

Alternatively, in the second application of the rule, the peculiar Or statement contains a disjunct which is itself an And statement. When we see these patterns, we can distribute the other conjunct (or disjunct) along with the main connective into the conjunct which is an Or (or, in the second application, the one which is an And statement). What was once a minor connective becomes the main connective. See here:

□ ∙ ( △ v ○ )       ∷       ( □ ∙ △ ) v ( □ ∙ ○ )

□ v ( △ ∙ ○ )       ∷       ( □ v △ ) ∙ ( □ v ○ )

Another way to look at this rule is to start from the right side of the four dots. Focus on that side and ask yourself this:

Q: What is “odd” or “funny looking” about the statement form on the right?

If you noticed a repeated presence of the □ claim, then you have a good chance of recognizing this pattern.

( □ ∙ △ ) v ( □ ∙ ○ )

( □ v △ ) ∙ ( □ v ○ )

We see here that the exact same statement (□) appears in both conjuncts (or disjuncts).

That’s odd. How did it get there?

A: It was distributed in.

So that means (since it’s four dots) that we can un-distribute it and isolate it. That’s what we’re seeing to the left of the four dots.

This is very handy when we want that □. After all, if the result is an And statement (see the first application), then we’re going to Simp(ly) grab it after the distribution.

NOTE: In this rule, the order of the component statements (the □ △ ○ ) does not change. Again, if we wish to switch the order of these statements, we have commutation to do that.

Exportation (Exp)

The rule of exportation applies to peculiar conditional statements. The form looks like this:

( □ · △) →○      ∷      □ → ( △ → ○ )

Exportation might look a bit confusing at first, but in our everyday lives we frequently find ourselves reasoning in this way. Look at the right-hand side of the four dots. You might recognize this pattern from a road map. If this were a trip we were planning, we might ask:

Q: How do you get to the town of ○?

A: You have to go through the town of △.

Q: Is that all?

A: No, you also have to go through the town of □.

Moral: You have to go through the towns of □ AND △.

So when we look at the left side of the four dots, this is exactly what we’re saying. You have to go through the towns of □ · △ to get to the town of ○.

An alternative way to think about exportation is in the name of the rule. Looking at the left side of the four dots we see that the antecedent is a compound—it’s an And statement. There are two things in the antecedent, so we can “export out” the right-hand conjunct (the △) into the overall consequent. The consequent then becomes its own little conditional with that same △ as its consequent (△ → ○).

A Word of Warning: Use care in how you think about what you see in this rule. On the left side of the four dots is a conditional whose ANTECEDENT is an And statement. We don’t care what the consequent is on this side of the four dots, and we cannot use this rule if the ANTECEDENT is a Conditional statement. We can only use it if there’s an And statement in the antecedent.

Also, on the right side of the four dots is a conditional whose CONSEQUENT is itself a conditional. That’s all that matters here. We don’t simply see any ol’ string of conditionals—we see a very specific pattern. After all, the following might be rightly called a “string of conditionals” in a sense:

( □ → △ ) → ○

However, you cannot use exportation on this form. Having a conditional in the antecedent doesn’t help. The little conditional we see in “a string of conditionals” has to be in the consequent.

Material Implication (MI or IMP)

The rule of implication applies to conditional statements (and to disjunctions). The form looks like this:

□ → △ ∷ ~ □ v △

Implication expresses the basic concept of bivalence as it applies to the antecedent of conditional statements. That antecedent is either true or it is false. If it is true, then we know that △ follows. If it is false, then we really don’t know anything except that it is false. So either ~ □ is true or △ is true. Simple.

Implication is an extremely powerful rule. IMP enables us to transform any conditional into an Or statement (and vice versa). So that means every strategy we have for proving Or statements is now applicable to proving conditionals (and vice versa).

We should also note that the right-hand side of the four dots is a bit misleading. To the right, we first see a peculiar looking Or statement. This Or’s left-hand disjunct is a negation, and that’s a tip-off that IMP may apply. However, this does not need to be the case. After all, consider this:

N v C

Can we apply IMP to this? Of course, we just need to “see” the negation hiding here. The rule of Double Negation makes this easy:

~ ~ N v C

Now we have a statement which fits the form of the right-hand side of the rule.

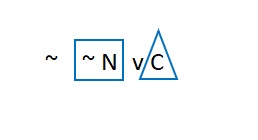
The result of using IMP on this would thus be as follows:

~ N → C

The moral of that story is that in truth, ANY conditional can be exchanged for an equivalent Or statement, and ANY Or statement can be exchanged for an equivalent conditional statement. You don’t need to actually have the negation present, as we saw through the use of DN to produce it. The shorthand rule for using IMP is the following phrase:

Negate the antecedent, leave the consequent alone.

Alternatively, you could say:

Negate the left-hand disjunct, leave the right alone.

Always leave the right-hand side of the statement you are Implicating alone. This will make applying IMP to any conditional or Or easy, regardless of whether an actual “~” appears or not.

Material Equivalence (ME or Equiv)

The rule of Implication applies to biconditional statements. There are two applications of the rule. The forms look like this:

( □ ↔ △ )       ∷       ( □ → △ ) ∙ ( △ → □ )

( □ ↔ △ )       ∷       ( □ ∙ △ ) v ( ~ □ ∙ ~ △ )

Finally! We have ways to access biconditional statements! There are two versions of this rule, so let’s nickname them to help memorize the form:

The “Name” version: Anything which is a “bi” has “two” in it. In this case, a “bi-conditional” has two conditionals buried in it. So we’re just unpacking those two conditionals. Since we really do have both of these, the two conditionals are joined with a dot.

( □ → △ ) ∙ ( △ → □ )

The Truth Table version: If you remember the basic conditions of truth for biconditionals, you know that there are two ways a biconditional can be true. Since we are assuming this biconditional is true, we can say that at least one of these conditions is true. This version of the rule simply expresses those conditions, and we use a “v” to join them because we don’t know which of these two conditions holds. It could be one or it could be the other.

( □ ∙ △ ) v ( ~ □ ∙ ~ △ )

With material equivalence, we now have a way to use every biconditional as a conditional. We’ll just unpack it with ME and then Simp out the one we need. The truth table version is handy when it comes time to prove a biconditional is true. After all, we really just need to prove one of the disjuncts, Add the other, and then use ME to assert our biconditional.

Second 5 Replacement Rules Problem Set

Second 5 Replacement Rules Problem Set [PDF, 40 KB]

Sub-Proof Methods

The next two “rules” are more akin to modifications of the existing methods we have already learned. Now, rather than passively accept the range of the primary scope line, we will actively initiate additional scope lines with their own limited ranges. Like the primary scope line, these secondary scope lines define a range under which statements can be treated as true.

The initial claim that starts the process is not being asserted as true—it is merely assumed for the duration of the scope line. The savvy student recalls that this is exactly the same as how our premises are treated—they are not proven to be true, they are merely assumed to be true for the purpose of the proof. So, schematically it looks roughly like this:

We have two reasons to initiate an assumption with its own scope line. One is to help us prove conditional statements. The other is to help us prove that an “assumed statement” cannot possibly be true. These two reasons are formally expressed in the following two sub-proof rules.

Conditional Proof (CP)

This rule builds conditional statements; it is a rule tailor-made to do one and only one thing: build conditionals. To use it, we initiate an assumption and draw out our secondary scope line. We then proceed as usual in a proof. The objective is to make our way down to the consequent of the conditional we want to prove is true.

Thus, the basic setup of a conditional proof is driven by the conditional we want to prove is true.

• Assume that the antecedent is true
• Then demonstrate that the consequent is true under this assumption

The form of the rule looks like this:

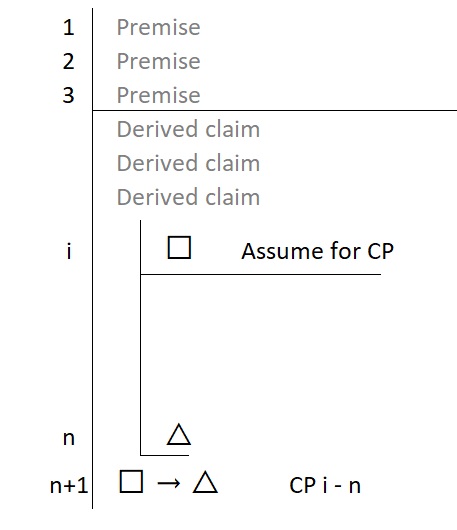
The method requires us to assume the antecedent and then get to the consequent.

The antecedent itself is NOT being proven true. We are explicitly noting that this is simply an assumption. So, our notation can be “Assume for CP.” Put differently, we might say that we suppose that it were true. So, our notation can be “Suppose for CP.” Either notation works fine. However, every other statement in the sub-proof does need to be fully justified in the usual ways.

Once we have arrived at a fully justified consequent, we close up the formal sub-proof. We call this “discharging the assumption.” On paper, we’ll draw a small line under the last statement in the sub-proof to show that it has closed.

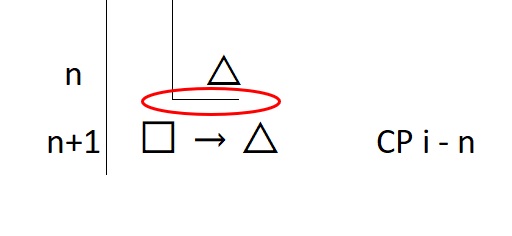
At the end of the day, we must discharge the assumption. We cannot claim to have done anything if we leave the assumption open, because every statement under it has only been proven true under this assumption. We don’t know what is true in the real world (i.e., along the primary scope line). We only know what is true if you help yourself to another statement which you already know may or may not be true—it’s only being assumed true for the purpose of this technique.

What is being shown as true in the real world is what we get when we discharge the assumption. We immediately write (along the nearest scope line) the claim □ → △. We know that arrow is true. Put differently, we know that the relationship between □ and △ in fact holds: △ really does follow from □.

One more note on the formal setup of CP: once you discharge an assumption, nothing contained within its scope line can be accessed or referenced directly. Hands off! So for example, the following would be a violation of this restriction:

In this example, the use of Conj attempts to reference line 7, but line 7’s truth is no longer secure once we discharge the assumption after line 9.

The savvy student may already understand why this restriction is important. If something follows from an assumption, there is no real guarantee that it is true outside the scope of that assumption. So relying on that statement is sketchy at best.

Once an assumption has been discharged (and it must eventually be discharged) we no longer have access to any of those statements.

Intuitively, CP is nothing more than a formal way to demonstrate what we mean in a conditional statement. “If the antecedent is true, then we can be assured that the consequent is true.” We are just showing this in a step-by-step process.

You may not realize it, but you very likely have practiced a verbal version of this same method at many points in your life. Think of a time when one of your friends didn’t believe that what you were saying was true. Like this:

You: Hey, I was thinking about going to the amusement park this weekend. Do you want to come along?

Bob: I don’t know, amusement parks aren’t really my thing.

You: I get that, but this park is really special. If we go, we’re going to have an amazing time.

Bob: I don’t know…

You: Look, let’s say we go. Do you know what we’ll see? They have some of the best rides in the country. Have you ever been on a roller coaster that has a 200-foot drop? It’s such an adrenaline rush, and the view from the top is amazing!

Bob: I guess that sounds pretty cool, but I’m not really into roller coasters.

You: That’s okay! You can do roller coasters, or you can do plenty of other things too. They have a fantastic water park section with some really fun water slides and a lazy river where you can just relax. Plus, there are lots of games and shows. Last time I went, they also had this incredible magic show that had everyone amazed.

Bob: I do like magic shows.

You: And the food is great too. They have this one place that sells the best funnel cakes and another spot with gourmet burgers. Trust me, if you go, it’s worth going just for the food.

Bob: Hmm, I do love good food.

You: Are you kidding me! You’re going to eat like a king! Plus, it’s a perfect way to take a break from the usual routine. We’ll spend the day outside having fun. We could even get some cool pictures and make it a day to remember. It’s going to be sunny and warm this weekend, perfect weather for it.

Bob: When you put it that way, it does sound like fun. Okay, I’m in!

You: Awesome! I promise you won’t regret it. We’re going to have a blast!

You go through all the steps that connect your assumption (we go) with your final consequent (we’re going to have a blast). You have now proven to Bob that it is true: If we go to the amusement park, we’re going to have a blast. Using conditional proof is nothing more than this laid out in a formal way. Here’s an example of this in symbolic form.

The completed proof looks like this:

Note that the conditional we want drives the setup: we assumed its antecedent and have set its consequent as our target statement to prove.

From here, the proof proceeds as usual. We have access to the assumption we made as well as all other undischarged assumptions. In the example, this includes all the premises (remember: the primary scope line is never discharged). All we need to do is prove that our next subgoal (i.e., the consequent) is true.

Once completed, the annotation for CP is slightly different than most rules. We reference the entire range of the sub-proof. So we use “–” to indicate the start and end of the sub-proof.

Initially, many students ask when they should consider using CP over other ways to prove a conditional (HS or IMP). That’s a fair question. There is no hard-and-fast requirement to use CP. However, the savvy student will consider the nature of CP. In using it:

1. We use a method tailor-made for proving conditionals—it’s like a toaster…that thing only exists to do one thing: make toast.
   So, when do you use it? Mostly, when you want toast
2. We get to play with another statement—we have more resources to use when we have an assumption that is temporarily true

You will find that CP greatly simplifies proofs. Sure, there are many ways to correctly finish a proof and to correctly prove a conditional to be true. However, as a general rule, unless an HS or IMP jumps out at you, you should give CP serious consideration any time you need to prove a conditional is true.

Nested Sub-Derivations

When we say you should consider using CP any time you need a conditional, we really mean it. Consider the following example:

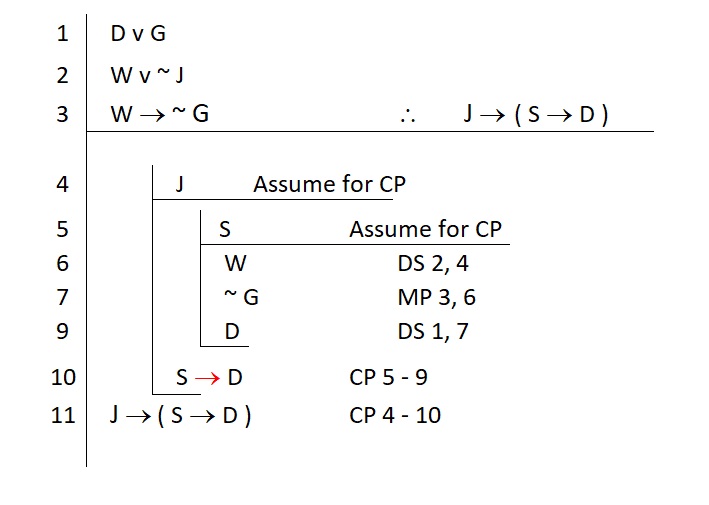
Our first sub-proof put us in good shape to prove our conditional. All we needed to do is prove that the consequent is true.

Q: What is the consequent?

A: It is a conditional statement (see the red emphasis)

Q: Do we have any tailor-made methods for proving conditionals?

A: Yes, we have conditional proof…

So we just started another CP. Nothing in the CP method prohibits this. Indeed, if we needed to prove another conditional, we would be free to use it yet another time.

Of course, making these assumptions always requires us to (a) know why we are making them, and (b) to formally discharge those assumptions.

Note that our justifications for each sub-proof begin and end with the relevant assumption and the relevant subgoal. Remember that outside each closed sub-proof we have no access to the statements inside. So for example, we may have a nested sub-proof that looks like this:

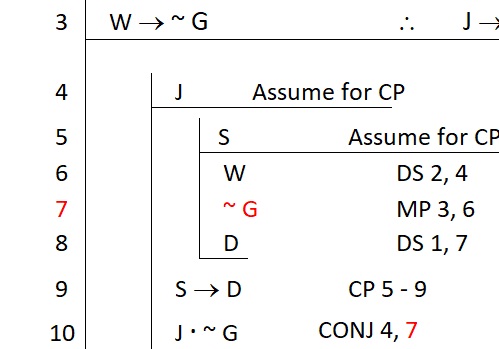
Here, we might be tempted to justify line 10 by reference to line 7 (a statement that appears in the tiny sub-proof). This would not be allowed, because by the time we get to line 10 we will have already discharged the assumption under which line 7 was established.

Of course, we are free to justify line 10 with any statement that appears above and to the left of it, so long as it is not bound by a discharged assumption. For example, the reference to line 4 is perfectly fine:

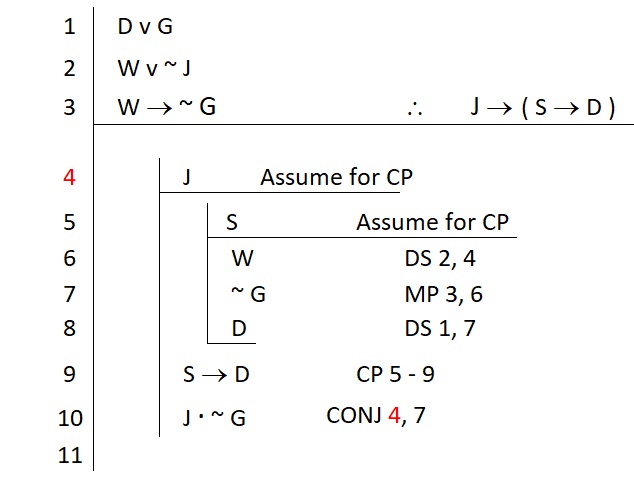
Line 4 is not under a discharged assumption; at the time of line 10 its scope is still open. So it is fair game for justifying line 10 (so too are all the premises if they were needed). Sadly for this proof, we would still need to find a way to justify the right-hand conjunct so that it was accessible for us to justify line 10. We would need to do something like this:

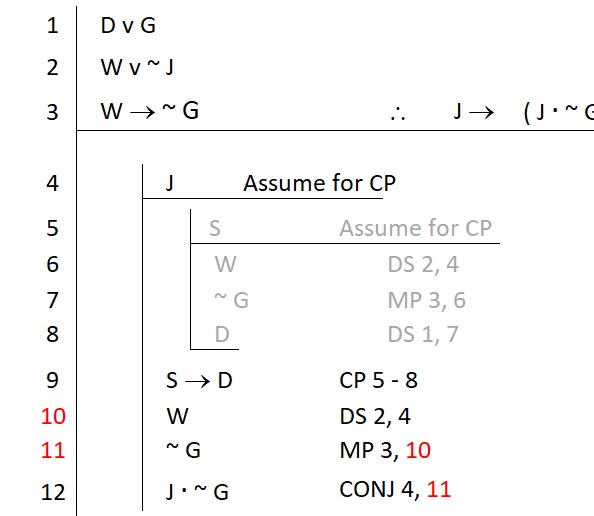
Here the red emphasis makes it clear that we had to repeat what we had done within the smaller sub-proof. This makes the claims on line 10 and 11 accessible to us after we had discharged the assumption that had previously closed off these claims.

If we had seen the need for these statements outside of the tiny sub-proof, we may have organized our entire strategy a bit differently to avoid the repetition. However, there is nothing inherently incorrect about the use of any of our rules in this example. The proof may look “ugly,” but it is correct.

Keep such formal constraints in mind when using nested sub-proof methods.

Conditional Proof Problem Set

Conditional Proof Problem Set [PDF, 36 KB]

Indirect Proof (IP) / Reductio ad Absurdum (RAA)

Indirect proof is also a sub-proof method. So, it adheres to all the same general requirements and restrictions that CP follows. The assumption we make is different and the goal is different, but the general way in which it works is the same as the CP sub-proof method.

The other name for IP is reductio ad absurdum. This name reveals the underlying strategy of this method.

Let’s say you want to diagnose a problem. You might start by making an assumption. Maybe the lights won’t go on because the bulb is bad. Let’s assume that to be true so we can test our hypothesis. If this assumption leads to some claim that simply cannot be true, some claim that is patently absurd, then there’s no way our assumption can be true. We would have to deny it.

For example, if we put that bulb in another socket and it lit up, we would know that the bulb is not bad. However, we just assumed that it was bad. So, we are forced into the claim that this bulb is both bad and not bad. That’s absurd! Our assumption must be false. So we can conclude that the bulb is, in fact, not bad.

This common diagnostic process is how reductio ad absurdum works. In logic, claims that cannot be true are called self-contradictions. They have the form: △ ∙ ~ △

These statements are logical falsehoods. They are always false, so the principle of bivalence tells us that the denial of them will be true. RAA relies on the notion that an assumption that validly led to such an impossibility must also itself be false. Thus, the negation of that assumption must be true. The form of the method looks like this:

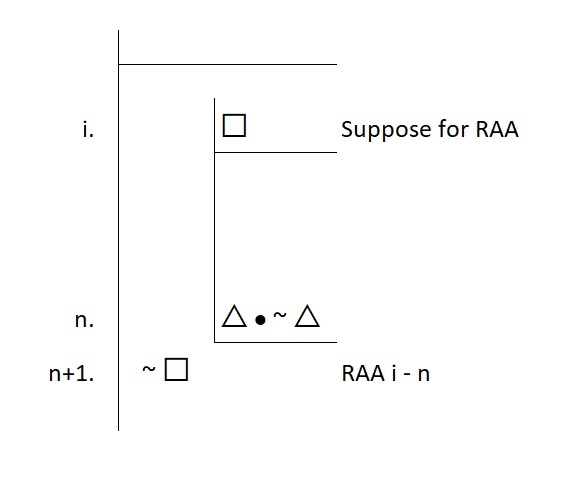
Strategically speaking, the setup of the RAA is simple. We know what we want. We want □. However, we could assume the denial of this □. We can suppose ~ □ is true. Should that lead us to a contradiction, then we will formally discharge our assumption and claim that absurdity must not stand! Thus, □ is indeed true.

Nice. But here’s the rub: while the setup is pretty easy, the target is not really well known. When we look at our new subgoal, we are left with nothing much to look at except the general form of △ ∙ ~ △. We have no idea what this statement will actually be, or even if it is simply one of a number of different statements that satisfy this form. Unlike conditional proof, a RAA strategy leaves us with little guidance on what to do next. We just know we need to figure out a way to produce something absurd. Anything absurd will do. Anything at all, including (but certainly not limited to) □ ∙ ~ □. We just don’t know for sure…

Consider the following example:

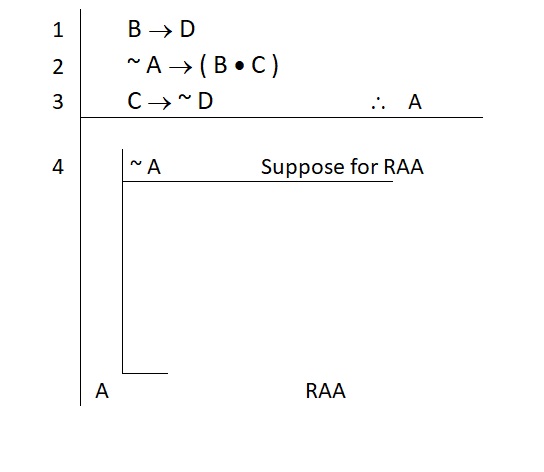
Our setup was clear enough. We wanted to prove that the atomic statement “A” is true, so we assumed the negation of it: ~ A.

From here, we need to hunt for things that look promising. RAA favors those who like to explore what the premises and their assumptions can offer.

In using a RAA method, until you get a clear line of sight on your contradiction of choice, you will be in a mindset of “what can I do with this?”

In our example, we made an assumption, and we should now consider if there is anything we can do with it alongside the other statements we have access to use. Every logician will go about this in their own way—each perspective yields different opportunities. So what your friend sees as useful may differ from what you see—and both of you may be correct. Again, RAA starts off as a bit of a fishing expedition. We’re just on the lookout for useful things…

We might spy this opportunity:

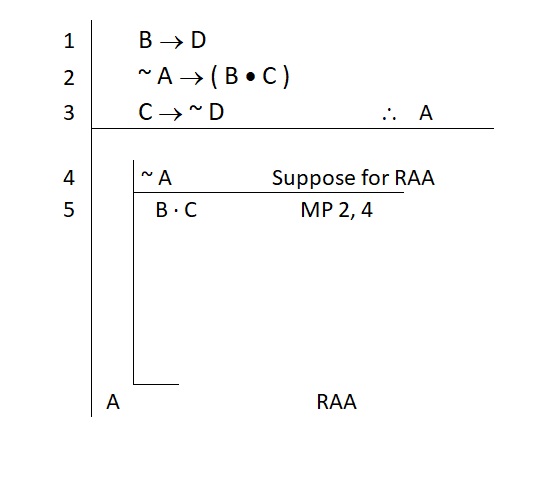
That assumption bought us a new statement. Can we do anything with it? Maybe this will help:

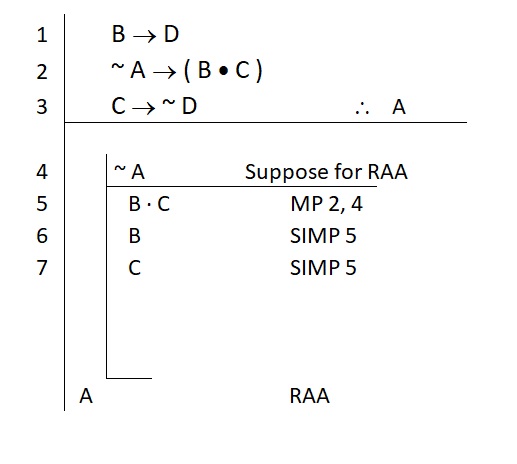
Is this going anywhere?

Don’t know.

What else can we do?

Wait! What about this:

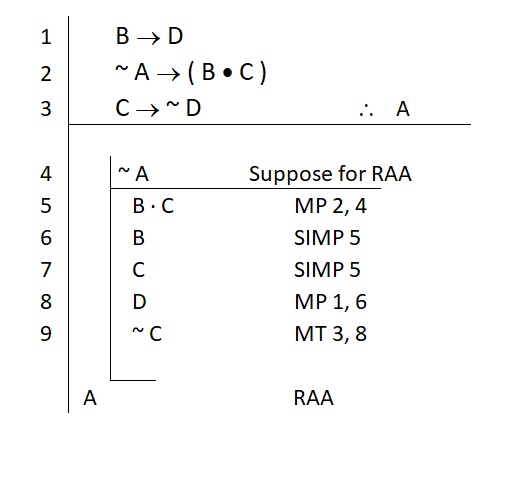
This is often how RAA goes. If you saw something different, great! Run it down. See if it pans out. Remember that the only requirement is to generate an absurdity. Your absurdity may very well differ from mine. [I suppose that’s something of a logic life lesson as well.]

My finished version looks like this:

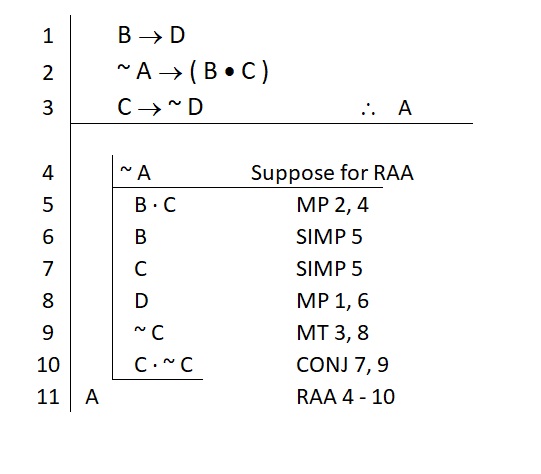
In this proof we arrived at one absurdity (C ∙ ~ C). One is enough. Under our assumption, something intolerable has been validly derived. Thus, our assumption must be wrong. We now formally discharge our assumption and assert that its opposite is true.

Note that in many problems we will assume that a negation is true. If that assumption proves to lead to an absurdity, then the statement it negates can be asserted as true. Like this:

1. Assume ~ M
2. Get to a contradiction
3. Discharge the assumption
4. End up with M

Alternatively, we can pop out of our formally discharged assumption with a double negation. Like this:

1. Assume ~ M
2. Get to a contradiction
3. Discharge the assumption
4. End up with ~ ~ M

Either wrap-up to a RAA is fine.

Last word on RAA. This method is extremely powerful. It is also extremely risky. Because we do not have a clear sub-proof to guide us, you can get lost for a very long time in a RAA effort. You will find CP often simplifies your life and makes proofs much easier—not so with RAA.

TIP: Use RAA as a last resort after you feel like more conventional strategies have failed you. Unless you very quickly sense that a contradiction will be readily found, hold off on pushing the panic button.

Indirect Proof (IP) / Reductio ad Absurdum (RAA) Problem Set

RAA Indirect Proof Problem Set [PDF, 36 KB]

Theorems

We’ll finish our section on sub-proof methods with a word on theorems in our symbolic language. A theorem is simply a statement which is logically true. Logically true statements are always true, regardless of any conditions of the world. They’re weird like that. Their truth is utterly non-dependent on the facts of the world. However, this also means that it should not matter what we know about the world to prove that they are true. Put differently, you don’t need to be given any pre-existing statements to treat as true to prove a theorem—you don’t need to rely on premises to support the truth of a theorem. So we prove theorems with no premises. Line 1 is blank.

Of course, by now you have been practicing the reverse method of doing proofs for weeks. You don’t rely on premises at all…do you…

You are a logician. Logicians rely on strategy!

To prove a theorem, you only need to understand what it is, and then generate a suitable strategy. At its deepest level, this game never depended on premises in the first place. This has always been driven by your goals. The most important logic life lesson:

Goals are primary. Where you landed in life and what you have to work with is secondary.

So take a look at a simple theorem like this:

~ ( J ∙ ~ J )

Q: What is it?

A: It’s a negation

Q: How do you prove negations?

A: The most straightforward way is to use RAA. Let’s assume that what it negates is true; if we find a contradiction, then by RAA we will have our negation

See? Strategy.

Every theorem is just an exercise in pure strategy. This theorem is easy to prove. The problem starts with only a conclusion—no premises are present. Like this:

We’ll set up our RAA as follows:

Now the task is to find a contradiction.

Well, that shouldn’t be hard…after all, we sort of assumed a contradiction to kick-start it. So all we need to do is formally demonstrate this is so under our assumption.

This was always going to be an easy proof. The theorem was denying an absurd statement in the first place. So, no wonder RAA successfully proved the denial of absurdity is true.

Of course, not every theorem is a negation. Consider the following simple theorem:

( E ∙ M ) → ( ~ G v M )

Q: What is it?

A: It’s a conditional statement

Q: Do we have any tailor-made methods for proving conditionals?

A: Yes, we have conditional proof…

The setup for a conditional proof does not require premises. The setup only requires knowledge of what you want. So we set it up as follows:

From here we now know that we need to show that the consequent ( ~ G v M ) is true. This is easy:

After a few of these, the savvy student realizes that proving theorems is actually quite easy. They will require the use of one of the sub-proof methods to get started. From there, the proofs follow the usual strategies.

Keep in mind that sub-proof methods have no restrictions on when they are used. In other words, similar to what we saw in nested conditional proofs, you may use a combination of CP and RAA within one another to get the job done.

Theorems Problem Set

Theorems Problem Set [PDF, 26 KB]