6 Truth Tables
We have seen how challenging it can be to evaluate arguments for their informal qualities. When we turn to evaluating their formal qualities, there are many tools at the logician’s disposal to ease the process. Truth tables are nothing more than a way to visualize the core concepts and formal properties of statements. As such, they also help us quickly evaluate arguments. In this sense, truth tables are nothing more than pictures we draw. We want a way to draw the concepts surrounding truth and possibility. So, if a picture is worth a thousand words, then a truth table is worth all possible worlds…
Given our commitment to bivalence, we know that there are only two possible truth values for any given statement, P: it can be either true or false. We have a way of writing this that is called a “truth table.” For an atomic sentence, the truth table is trivial, but when we look at other kinds of sentences, their truth tables will be more complex.
The idea of a truth table is to describe the conditions in which a sentence is true or false. We do this by identifying all the atomic sentences that compose that sentence. Remember that larger statements are composed of truth-functional logical operators—so the truth of any compound will depend on the truth value of the smaller atomics out of which the compound is made.
Setting Up a Truth Table
The set up for a truth table is simple. We will only have four quadrants to our table, so only two lines need to be used to organize the information we need. This will look like this:
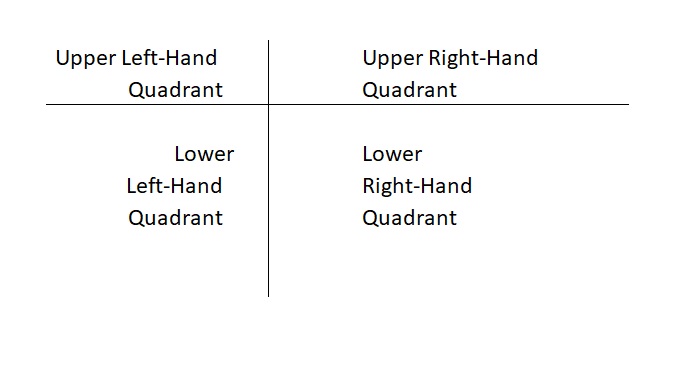
You might even think of truth tables as being divided in two halves. On the left is the basic information we need, and on the right is the statement(s) we want to evaluate and the information about it.
So, on the left side, we stipulate all the possible truth values of these atomic sentences and write these out. On the right side, we then identify under what conditions the sentence (that is composed of the other atomic sentences) is true or false.
The idea is that the sentence on the right is dependent on the sentence(s) on the left. So the truth table is filled in like this:
| Atomic sentence(s) that compose the dependent sentence on the right | Dependent sentence composed of the atomic sentences on the left |
| All possible combinations of truth values of the composing atomic sentences | Resulting truth values for each possible combination of truth values of the composing atomic sentences |
One important note before we go any further. When we say we will fill in the upper left quadrant with all the atomic statements that compose our statements on the right, we must follow one simple rule: list the atomics in the SAME order in which they appear in the upper right (when you read from left to right). We do not put them in alphabetic order, and we do not spell out funny words with them. We always put them in exactly the same order in which they appear in the upper right (skipping any repeats).
We stipulate all the possible truth values on the bottom left because all of the logical properties that we learned are defined in terms of different possibilities. When you hear most folks talk about this or that being “possible,” they are doing little more than expressing their own uncertainty or ignorance (e.g., “I don’t know! It’s possible.”). This is not how a logician sees it. For us, the claim that “X is possible” is a claim of knowledge. We know. Or rather, we will know for certain that something is possible—because we took the time to check. That’s what the lower left part of a truth table provides: a record of every possible combination of truth values.
For an atomic statement, the total number of possible truth values is merely two: true or false. So, this means that if we wish to evaluate a compound statement that is made up entirely of just that one statement, there will also be only two possible combinations of truth values. We can start here, since this will be easy to do while illustrating many key features of how truth tables are set up.
So let’s evaluate the following statement:
~ G
We start by setting up our truth table, first by laying out our four quadrants and placing the atomic statement(s) in the upper left corner.
| G |
Now we will put the statement(s) we wish to evaluate in the upper right corner.
| G | ~ G |
Now we list all possible truth values for the atomic(s) in our table and number these possibilities:
| G | ~ G |
| 1. T | |
| 2. F |
The statement we want to evaluate is made up of this atomic, so we can transfer over the possible truth values we listed on the left over to the right side, where we see the same atomic.
Like this:
| G | ~ G |
| 1. T | T |
| 2. F | F |
I know this sounds a bit redundant right now, but that is only because this table is exceedingly simple. When we get to larger statements and larger truth tables, we will be rewarded for taking time on this very simple step.
Now we can consider the impact that our logical operator has on the truth of the overall statement. Negations are easy—they simply invert the truth value of whatever statement they deny. When G is true, denying that claim will be false. When G is false, denying that claim will be true. So, we put these inverted values directly under the ~ symbol. Like this:
| G | ~ G |
| 1. T | F T |
| 2. F | F T |
This is a bit messy, so we will find it very helpful to clearly indicate which (if any) logical operator is the main connective of the statements we want to evaluate. Remember what we said about the main connective: one of its important qualities is that it is the bearer of truth for the statement. So when we indicate its importance on the truth table, we are graphically showing the truth value for that compound statement. We can either draw a small arrow over the main connective, draw a clear box around it, or both.
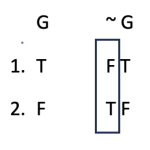
I prefer to use a box without the arrow, but as we go further you may find that different ways of marking your table work especially well for you. You and/or your professor will come up with an agreeable method.
Now our truth table is complete. We have shown every possible relevant scenario in which the truth value of ~ G can be established. We call these scenarios “cases” or “possible worlds,” and numbering them will help us to refer to them later, when we must justify our evaluations.
The completed table is nothing more than a picture of possible truth values. This can be used to answer questions about the statement we wanted to evaluate. We’ll discuss this later, but for now just note that we need to first learn how to construct truth tables. Their importance will be discussed once we know how to set them up.
So far this has been pretty easy. However, if we have a compound statement to evaluate that has another atomic, then we must add that atomic statement to the upper left side. For example:
A v ~ G
This doesn’t increase the number of possible truth values for the added statement; however, the number of combinations of truth values has increased.
For example, what are the possible combinations of truth values for A and B? After a bit of thought, most folks will be able to figure out that there are four possible combinations:
A is true, and G is true
A is false, and G is false
A is true, but G is false
A is false, but G is true
If you figured that out, good for you. Now what happens if we add a third atomic statement? For example:
M → ( A v ~ G )
Now we have to come up with every possible combination of truth values for those three atomic statements.
Q: How many possible combinations are there?
Q: What are they?
Your job is to answer both questions. Do it correctly, without fail, and do it quickly.
Got it already?
How about now?
No?
Well, the answer to our first question is 8 combinations. Now, quickly tell me what those 8 combinations are and don’t mess it up. Also, don’t repeat yourself…
Go!
No?
Okay, you’re going to have to get good at doing this…especially when we add a fourth atomic statement. Like this:
( H v M ) → ( A v ~ G )
Remember what you have to do. Answer the following questions:
Q: How many possible combinations are there?
Q: What are they?
Go!
Maybe you figured this out, but the answer to our first question with four atomics is 16 possible combinations. And yes, you have to tell me what they are and put them in your truth table (lower left quadrant). Sounds like fun.
If you don’t think this is fun, you just haven’t learned the method yet. We have a simple way to do this—really simple, as in a mechanical way to generate the answers that requires hardly any thought at all. How about that for a combination: guaranteed success + little mental effort
Ready? Here’s how we do it.
FIRST STEP: Count the number of atomics. You will double the number of possible combinations every time you add an atomic statement.
Start with one atomic: you have two possibilities (T/F).
Add an atomic (now 2 atomics total) and double the possibilities: from 2 possibilities to 4 possibilities.
Add an atomic (now 3 atomics total) and double the possibilities: from 4 possibilities to 8 possibilities.
So on and so forth. Remember this phrase: “double it up”
That tells you how many cases (or possible worlds) you must account for in your table. Now that we know, we need to detail those cases and list them in the lower left quadrant of our table. This turns out to be surprisingly easy.
SECOND STEP: Find the atomic snuggled up against our vertical line. You will simply alternate T and F under it for as many cases as the table requires. Like this:
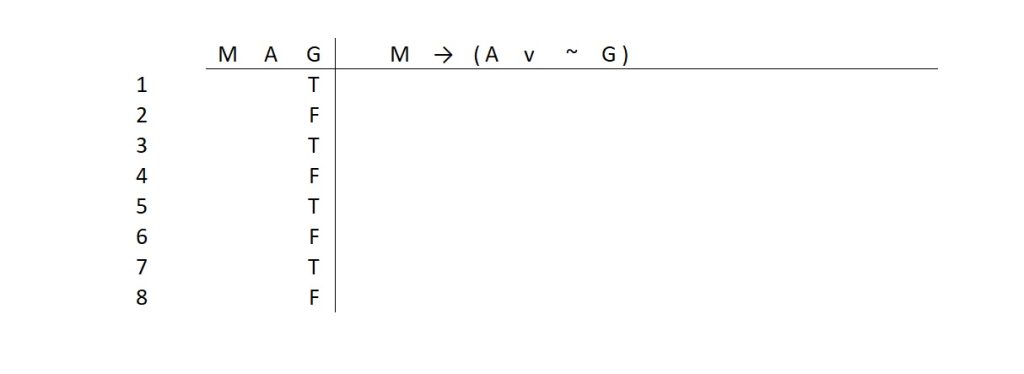
That’s not hard. Now slide over one atomic and “double it up”: You just alternated T and F every other line, so alternate every other two lines. Two true, two false, two true, two false…until all cases are completed. Like this:

Now slide over one atomic, and “double it up”: You just alternated T and F every two lines, so alternate ever four lines. Four true, four false, four true, four false…until all cases are completed. Like this:

Since we only have 8 cases in this table, this is done in a single pair of four true / four false. However, if we had a table with 16 cases, we would see this pattern repeat more. We would also slide over to our last atomic, and once again “double it up” (alternating T/F every 8 lines). The method chugs along until we are done with all of our atomics. All we have to do is remember three rules:
Rule 1: The number of atomics is used to determine the number of cases (possible worlds)
Rule 2: Start with the atomic closest to the vertical line
Rule 3: “Double it up”
The rest of the table requires a bit more knowledge, but the initial set up is pretty mechanical. I should note that Rule 2 is just a convention. There is nothing logically necessary about starting with the atomic next to the vertical line. However, there is great advantage to holding this as a conventional rule for all of us to follow. This makes it easy for us to communicate the information on our table to others who are working on the same problem.
Communicating information is critical to justifying your evaluations. So, when you are asked to evaluate a statement or an argument and justify your findings, you will refer to a case (or cases) to do so. If you are communicating in your own “unique” way, the chances are good that you will not get credit for your answer because everyone else is looking at a different line than the one you claim supports your answer.
When we all set up our tables with the same conventions, we are all able to communicate clearly and precisely. Put differently, there are no unique snowflakes in logic. We all adhere to the same principles. So, the faster we get on board with the same methods, the easier it is to check that we are following those principles.
THIRD STEP: Now that we have identified and exhausted every possible combination of truth values for the atomic statements (that make up the statement[s] we want to evaluate), we can just transfer those values over to the lower right-hand quadrant. Like this:
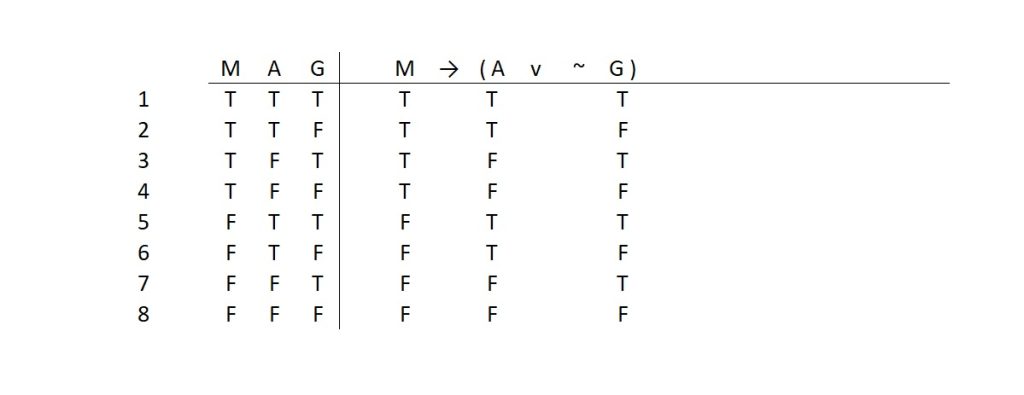
This might sound like a lot of redundant work, but this will make it very easy to complete the table. Before we can do that, we need to know how our logical operators impact the truth values of the component statements. We just saw this with negation, so let’s review that and look at the rest of our logical operators.
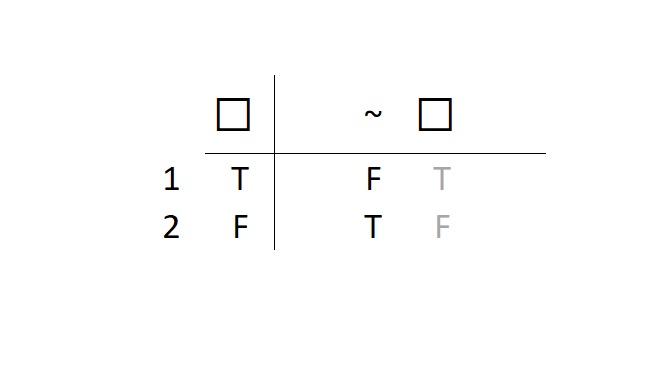
Negation
Negation is simply a denial. So as we saw, you simply invert the value of whatever is negated.
A Note on Annotation
In the above image, we are using our familiar □ (and later △ for the other operators) to indicate that a negation may apply to any statement at all, be it an atomic or a compound. However, we also used the □ (and later △ for the other operators) in the upper left-hand quadrant of the truth table. While □ and △ are our preferred statement variables, the reader should note that in this quadrant they can only ever be atomic statements. We never put compound statements in the upper left-hand quadrant of a truth table. In this quadrant, □ and △ can only represent atomic statements, whatever they are for the statements we wish to evaluate.
Conjunction
The conjunction is a union of two assertions. So think of this as a promise: I promise that we will do this and we will do that. To keep my promise (i.e., to ensure I speak the truth), I must fulfill both components. In other words, both sides need to be true in order for such a promise to be kept.
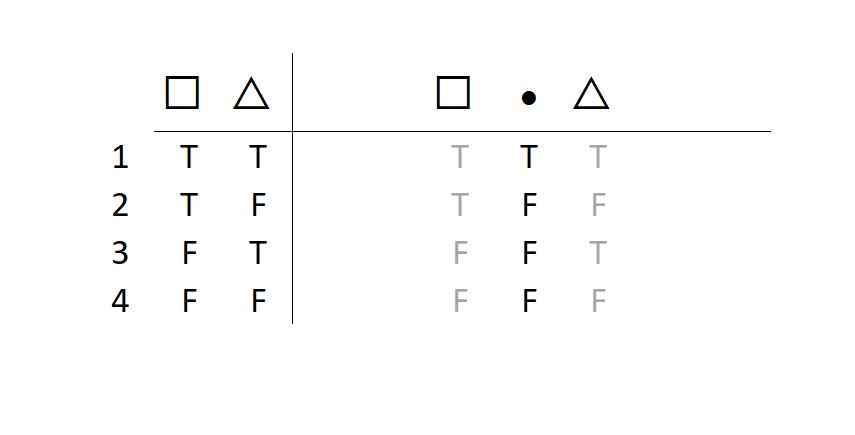
Note that conjunctions are typically false. It really is hard to keep such a promise.
Memorizing the basic conditions of truth for conjunctions is easy—both sides have to be true for the conjunction to be true (any false conjunct makes the whole thing false).
Disjunction
The disjunction is a weak expression of possible options. Go back to the notion of keeping a promise. If I promise that at the very least, we will do this or we will do that, well heck, it’s kind of easy to keep that promise. I can claim success in any of three scenarios: (1) we did this, (2) we did that, (3) we did both.
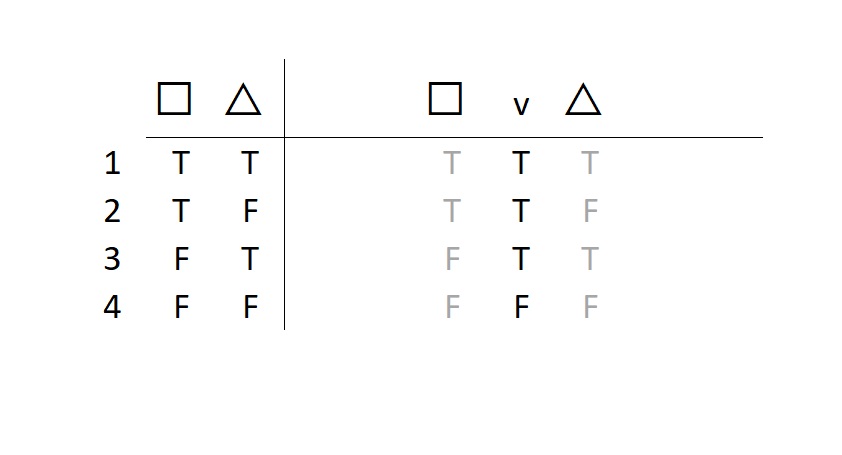
Note that disjunctions are typically true. TIP: If you’re going to make a promise, make it an Or-promise.
Memorizing the basic conditions of truth for disjunctions is easy—both sides have to be false for the disjunction to be true.
Material Conditional
The material conditional is a special relationship. We could (and do) casually call it a conditional, but the truth is that this is a logically specific relationship that is often quite different than what most people think of when they think “conditional.” Thus, if you struggle with this, keep calling it a “material conditional” so that you remember it is a technical term and a special kind of conditional.
A material conditional is not a claim of causality, nor does it entail any special temporal elements (like “this happens before that”). Many English conditional expressions do include these extra senses of the words, but this is not translated over to the logical operator we know as the material conditional. What our conditional does is nicely capture the relationship of necessary or sufficient conditions. So, let’s consider a story:
My dad used to make promises that were dependent on me doing my chores. I was the family dishwasher. I also liked to go rent movies (when there were movie rental stores and we didn’t have streaming services). So, dear old Dad would often promise, “If you do the dishes, we’ll go to rent movies.” Grand idea Dad! Put the ball in my court.
On some days, I did the dishes. On other days, I dropped the ball and didn’t do dishes. So what do you think dear old Dad did? Well, on some days, Dad took me to get the movies, and on other days he did not.
Q: On which days can we accuse Dad of speaking falsely?
Let’s consider only the days I did the dishes.
Day 1: He takes me to get movies. Yes! Dad spoke the truth!
Day 2: He didn’t take me to get movies. What the!?! Dad lied to me…I can’t believe it, but he spoke falsely.
Now let’s consider only the days I did not do the dishes.
Day 3: He takes me to get the movies anyway. Can I really be mad at Dad? Nah. (more on this in a bit)
Day 4: He didn’t take me to get movies. Well, what was I expecting? I mean, after all, I didn’t do the dishes. Can I accuse Dad of lying? No. So I’ll accept that Dad spoke the truth.
If you had to do the dishes in your house, then the material conditional starts to make sense. The trouble for some is the Day 3 scenario. I did NOT do the dishes, so what am I to make of Dad taking me to get the movies anyway? I feel like he misled me. But did he? What was it that Dad said?
If you do the dishes, then we’ll go rent movies.
From our work on translations, we see that “doing the dishes” is in the antecedent position (the □). This means that doing the dishes is in the place of the sufficient condition—it is supposed to be what logically guarantees that the △ claim is true. Also from our work on translations, we can see that this means that doing the dishes was not put in the place of the necessary condition (that’s the △ part, and in this case it is the claim about going to get the movies). Now we can go back to Dad.
Q: Did dear old Dad ever say doing the dishes was necessary?
No, he did not. He said it was sufficient (he never said it was necessary). So, when he takes me to get the movies even though I did not do the dishes, he did not propose a false promise. He never said that doing the dishes was necessary for getting the movies; he merely assured me it was sufficient to get him off the couch to drive over there. I may have heard him incorrectly—that’s always a strong possibility—but I cannot accuse him of misleading me simply because I failed to listen carefully. That shortcoming is on me.
Thus, the basic conditions of truth for the material conditional are as follows:
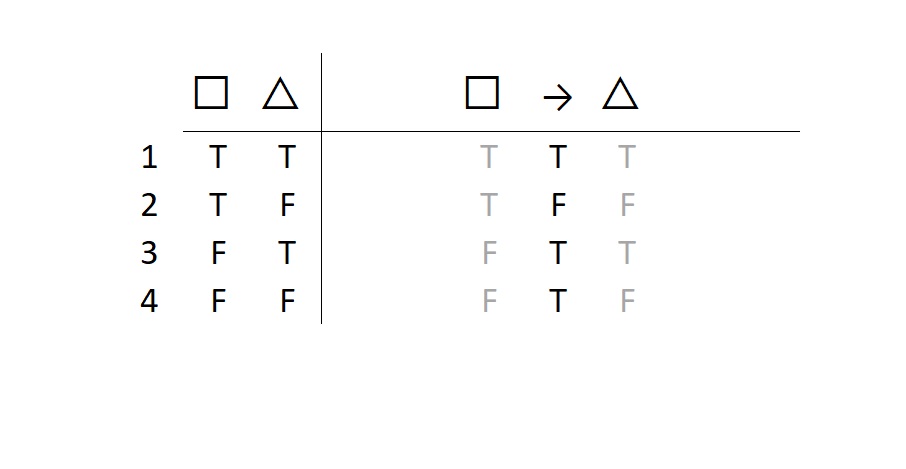
The easy way to memorize the basic conditions of truth for the material conditional is to remember that you can really only pin a falsehood on it when the antecedent, □, is satisfied (i.e., is true) but the consequent △ was not delivered (i.e., is false).
Material Biconditional
Remember that biconditionals are what many people hear when someone says a conditional statement. They hear a very tight relationship between both clauses (the □ and the △ ). Our story of doing the dishes illustrates this well. We may have heard Dad make a biconditional promise. We thought he was saying:
I’ll take you to get the movies if and only if you do the dishes.
That sounds like a Dad-promise. If he had made that promise, then we would expect the truth of his promise to look different than what we saw with the material conditional. And so it is.
![]()
Now we see in Case 3 (a.k.a. “Day 3” in our story) that there really is something shifty about Dad’s promise if he was planning on going to get the movies all along. In making this biconditional promise, he spoke falsely! Sure, I may not mind (I got the movies), but I sure can’t trust what that guy says. He said doing the dishes was both sufficient and necessary. How can that be true! How can it also be a necessary condition if he gets the movies anyway? Answer: it can’t; Dad speaks with a forked tongue.
The easy way to memorize the conditions of truth for a biconditional is to remember:
Biconditionals are true when both sides share the same truth value, false if there is a difference on each side.
Overview of the Basic Conditions of Truth for the Logical Operators
We can capture all of this information in a single truth table for easy reference. You need to have this in your back pocket. We’ll use “A” and “B” as placeholders for □ and △ to keep our table small. This is just a quick reference table that you must memorize:
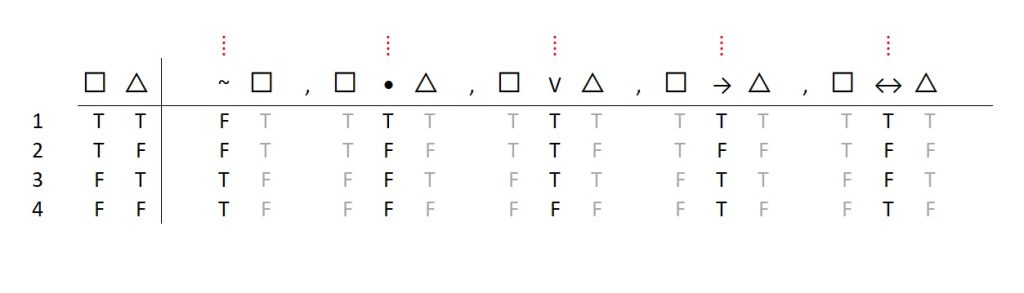
Calculating Truth Values for Statements
Have you memorized the truth table for the basic conditions of truth for all of the logical operators? If not, read no further. Stop what you are doing. Go back and reread. You must memorize the truth table for the basic conditions of truth of the logical operators. If you haven’t done so, then from here on out, you are really wasting your time.
I know that culturally speaking, many people look down on rote memorization as an approach to learning that is somehow stultifying and soul-crushing. And sure, rote memorization can be soul-crushing if it’s over-emphasized. But sometimes there is just no other way. Sometimes, as with much of the work in doing truth tables, it is actually soul-strengthening. Memorizing information requires you to focus. It can also feel good to flex your memory and see what it can do. If you don’t memorize the truth tables, you will likely find logic to be confusing and depressing. If you do memorize them correctly, you will find much of what follows to be really easy.
One hugely important aspect of sentential logic is the calculation of truth values. Once you’ve memorized the truth table definitions for the operators, this turns out to be incredibly easy to do. It can also be somewhat relaxing. Just think of yourself as a mindless computer that takes certain inputs and generates certain outputs.
Consider the following statement:
( P → Q ) ↔ ( ~ R → Q )
Earlier we saw that sentential logic is truth functional, which just means that the truth value of any complex statement (such as this one) is determined by the truth values of the simple statements it contains. The basic idea of truth functionality is simple: If you know what truth values to attach to the atomics in the statement above, then you can easily figure out what the truth value of the whole statement must be.
In order to see how this works, let’s just stipulate:
P: true
Q: true
R: false
What would the truth value of the whole statement be? The statement as a whole is a biconditional, since the main operator is a triple bar.
( P → Q ) ↔ ( ~ R → Q )
If we knew whether the chunk on each side were true or false, then we could consult the truth table for the triple bar to see what the the truth value of the whole statement must be. (And that is why it’s so important to memorize the truth table definitions for the logical operators.)
So, let’s take each chunk on its own. The chunk on the left is:
P → Q
We’ve stipulated that “P” and “Q” are both true, so “P → Q” must be true. So the left-hand chunk is true.
( P → Q ) ↔ ( ~ R → Q )
T
The right-hand chunk is just a bit more complicated. We know that “Q” is true. We’ve also stipulated that “R” is false. But that means that “~ R” is true. Since both “~ R” and “Q” are true, it follows that “~ R → Q” is also true. So the right-hand chunk is true as well.
( P → Q ) ↔ ( ~ R → Q )
T T
Now recall that a biconditional statement basically asserts that the chunk on the left and the chunk on the right have the same truth value. Here that is indeed the case: the left-hand chunk and the right-hand chunk are both true. So the whole statement is true. We can indicate this by placing a “T” under the main operator.
( P → Q) ↔ ( ~ R → Q)
T T T
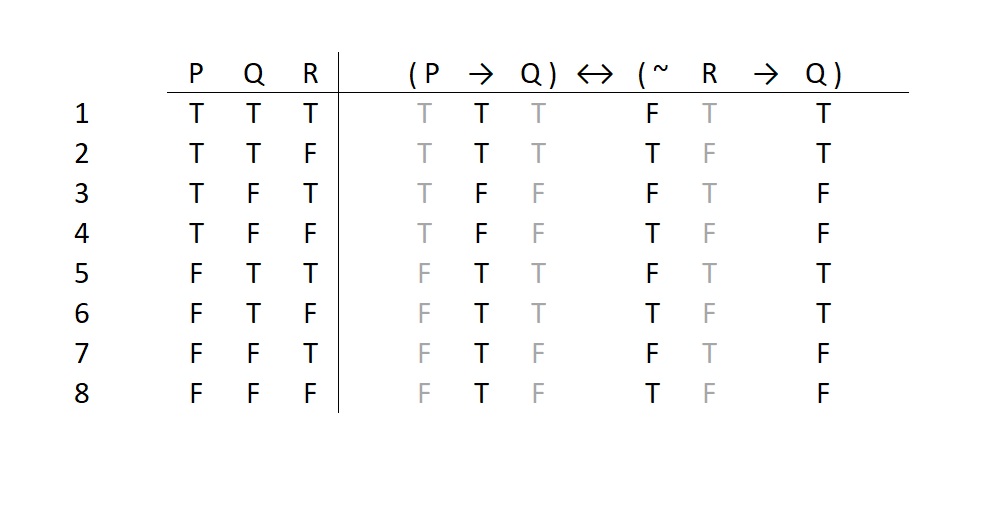
One reason why it’s important to practice these truth value calculations is that this is the key to filling in truth tables for propositions. Suppose we wanted to do a full-blown truth table for the above statement. It would start out looking like this:

Here we have already filled out the lower left quadrant with all possible combinations of truth values for the three atomics. We have also transferred those values over to the lower right quadrant for easy reference. Now we need to work through the logical structure of the statement as just discussed.
Working through Logical Structure
The first thing we need to do is mark the main connective and/or its eventual column. This helps us recognize the main components of the statement. Without knowledge of the main connective, you are lost. You have zero chance of successfully completing the table. So best to review that concept.
Practice your statement trees until you are very, very good at recognizing the logical structure of a statement. When you do a truth table, you are effectively working your way up through a statement tree: starting with the truth values for the atomics, then moving up through the statement, until you finally get to the very last operator to create the overall statement.
We start on our table by transferring those truth values to the atomics. This has been done above. So next step is to move on to the logical operators who join together or apply to nothing more than atomics. We can start with the left side of the biconditional.
The left side is a conditional statement. So the truth of this side will conform to the general conditions of truth for material conditional statements (which, of course, you have memorized by now). We indicate the truth value of this little conditional by putting its truth value directly under the arrow. Like this:

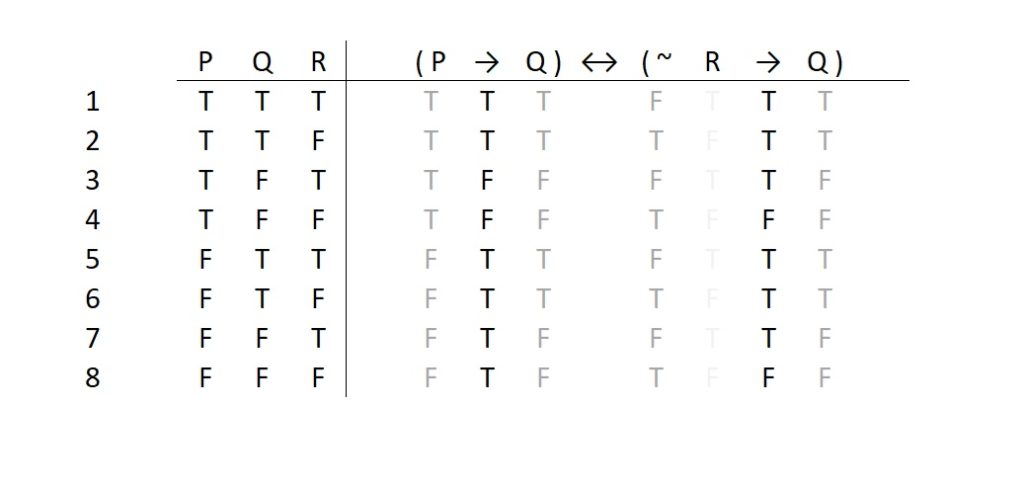
The next statement we would like to do is the right side of the biconditional. This too is a little conditional statement. However, this arrow joins an atomic and a negation. So, we cannot fill in that arrow until we know the truth value of the antecedent. Put differently, the right side has the following form:
□ → △
We will know the truth of that condition when we know the truth values of □ and △. The △ is an atomic, but the □ is a compound statement. So we cannot fill in the → column until we have a proper column for □.
In this case □ is a negation (specifically, inside the box is the statement “~ R”). Fortunately, this tilde applies directly to an atomic statement. So we can fill in the column for the ~.
Now we have the right side of the biconditional ready to complete. Our column under the tilde bears the truth of □, so we use that column along with the column under the “Q” to determine the truth values in the column under the right side →.
Our table is almost done. We can now see the column of truth values under each side of our biconditional. These two columns will be used to determine the column of truth values under the ↔.
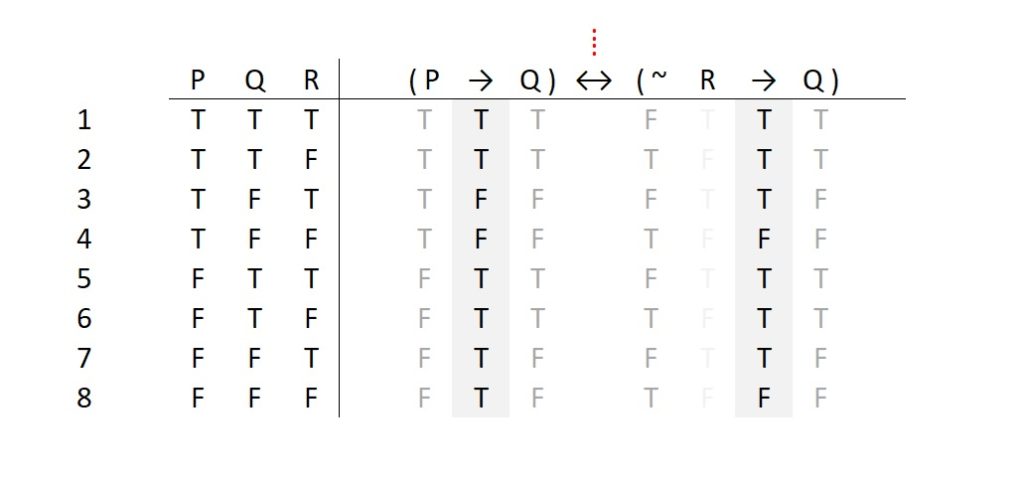
Of course, we have memorized the basic conditions of truth for the ↔, so this should be easy.
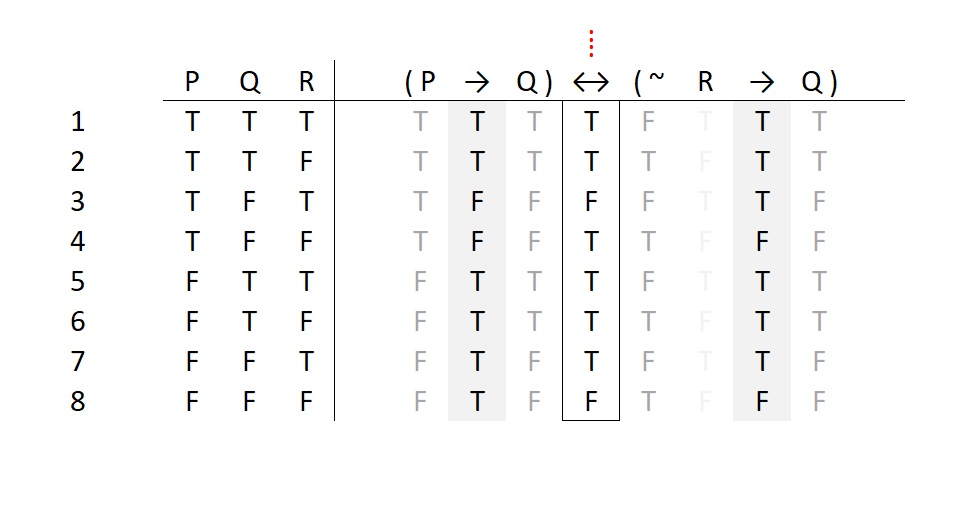
Now we have a complete picture of every possible case in which this statement is true and when it is false. The obvious question is: What are we going to do with this picture?
Using Truth Tables to Evaluate Logical Properties
Recall in Chapter 1 that we learned about important logical properties of statements. The savvy student remembers that all of these were defined in terms of possibility. So, naturally a truth table is an ideal tool to use for these properties.
Evaluating Individual Statements
The truth table we just built demonstrates every possible outcome for our previous sample statement:
( P → Q ) ↔ ( ~ R → Q )
Now we can ask questions of possibility. The first, and easiest, might be:
Q: Is this statement a logical tautology, contradiction, or contingent statement?
If you don’t remember what these properties are, here’s the cheat sheet version:
Tautology: a statement which is true under all conditions
Contradiction: a statement which is false under all conditions
Contingent statement: a statement which is true under some conditions and false under other conditions
A truth table provides us with “the conditions” that are important. We call these the “cases” or “possible worlds.” So each numbered case represents a specific condition of a possible world. When we look at a truth table, we are looking at the statement’s main connective column to answer this question.
Q: What do you see in the MC column? Is it all Ts, all Fs, or is it a combination?

We see that there is a combination of truth values. We don’t see a straight column of nothing but Ts (nor a column of nothing but Fs). If we did see a pure column of Ts, we would say this statement cannot be false; it is always true under all conditions (i.e., it’s a tautology or logically true statement). We would say the opposite if it were a column of pure Fs (i.e., it’s a contradiction or logically false statement). However, in this case we do not see those kinds of columns. We see a column in which sometimes the statement is true and sometimes it is false. So, we say that the statement is a contingent (or logically indeterminate) statement.
We might even go deeper into this table. If a friend doubted that this statement is ever true, we can provide them with a very specific set of conditions in which the statement would indeed be true. We can point to specific cases in which it is true. This can give us some sense of what the world must look like in order for the statement to be true or false.
Evaluating Sets of Statements
Many times, we want to know something about a group of statements. They may not even be an argument, or they may be small parts of an argument. No matter, we just want to know things about a given group. Truth tables can help us explore the logical properties of these groups.
Logical Equivalence
For example, consider the following:
Your friend makes a claim, then later says something different, but insists they said the same thing. In the morning your friend said, “Sure. If I go to the store, I’ll get some milk.” In the afternoon, your friend said, “Okay already! Either I don’t go to the store, or I’ll get some milk.” You think your friend is changing their story to suit themselves. But your friend may defend themselves by insisting that even though they said it differently, their second statement really meant “the same” thing. Well, does it?
A truth table can discover if two statements are logically equivalent. Again, if Chapter 1 content does not spring to mind immediately, here’s the cheat sheet version:
Logical Equivalence: two statements are logically equivalent if and only if they always have the same truth value as one another under all conditions
Since a truth table demonstrates all conditions, let’s go check the table.
We need to first translate our friend’s statement. This will do:
If I go to the store, I’ll get some milk.S → M
Either I don’t go to the store, or I’ll get some milk. ~ S v M
We can put multiple statements in a truth table’s upper right-hand quadrant by simply distinguishing them with commas. Like this: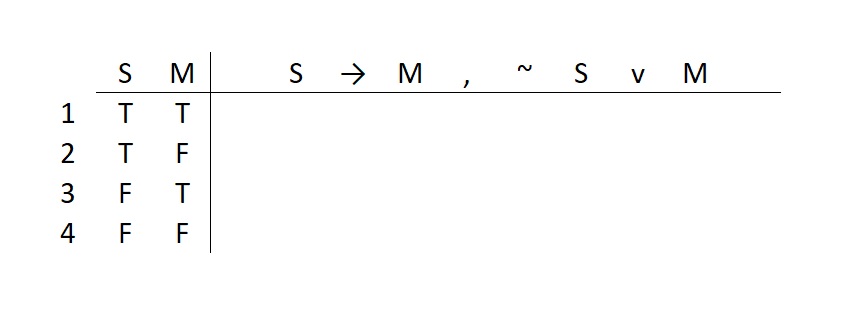
With only two atomics, this is a small truth table. The finished version looks like this: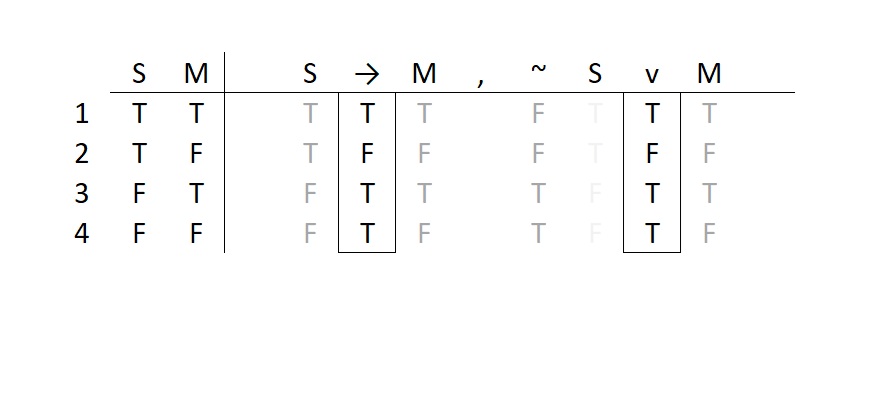
With a complete table we can look at the two columns under the main connective of each statement.
Q: Are they identical columns, or is there at least one variation in the truth values?
Now we can see that our friend really did say the same thing, insofar as their statements reflect the same account of the world. These two statements will always have the same truth value under any and all conditions.
CAUTION: Truth tables can be used this way only if we put both statements in the same table. You cannot reliably make one table for the first statement and another table for the second statement. This would run the risk of demonstrating very different possible combinations of truth values (i.e., different possible worlds). If this happens, we cannot make accurate claims about what is and is not possible. We must have all statements under evaluation in a single truth table to make those judgments.
Logical Consistency and Inconsistency
Let’s look at our other concepts for groups of statements. Remember logical consistency and inconsistency? No worries, here’s the cheat sheet version:
Logical Consistency: a set of statements is logically consistent if and only if it is possible for all members of the set to be true under the same conditions
Logical Inconsistency: a set of statements is logically inconsistent if and only if it is not possible for all members of the set to be true under the same conditions
Truth tables make short work of any question regarding these concepts. Let’s look at an example.
Consider the following statements:
~ K → W
~ ( W v K )
W ∙ K
Q: Are these statements logically consistent or are they inconsistent? When we put them all together in a truth table, we get the following:
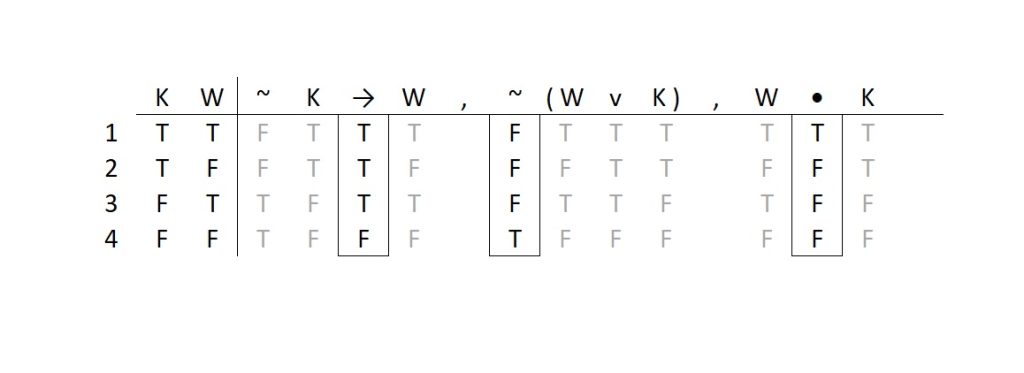
Our question is in regard to consistency, so we need to look at the columns under the main connective for all three statements. We look across the table, case by case, at each truth value under the main connectives. We are looking to see if there is any case (at least one) in which all three statements are true. This would demonstrate that it is possible for them to be true under the same conditions.
In this case, we do not see a single case in which all statements are true. That is, we never see the possibility of all statements being true, i.e., it is impossible for all members of this set of statements to be true under the same conditions. The set is inconsistent.
Let’s try another example. Consider the following statements:
~ B v E
~ ( E v ~ M ) → ~ B
M ∙ ~ E
Q: Are these statements logically consistent or are they inconsistent? When we put them all together in a truth table, we get the following:
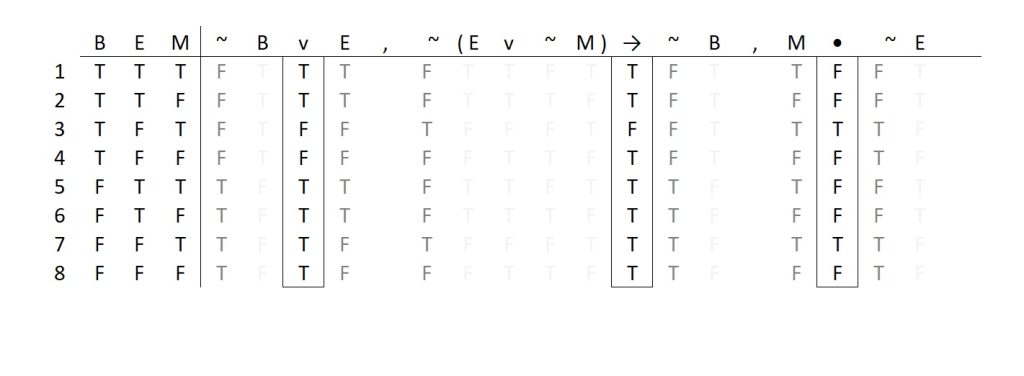
Again, we look across the table to read for consistency, focusing only on the main connectives of the three statements in our set. Going case by case, we see that it is rarely the case that all three statements in the set are true under the same conditions. This almost never happens. Rarely, but not impossible!
Indeed, in case #7 we see that it is possible for all three statements in our set to be true under the same conditions. What conditions? The condition of the world in which B and E are false while M is true.

So this set is logically consistent. Our justification would be “case #7” (or any other case in which this condition was met, if it were met by multiple cases). Note that since consistency merely requires “the possibility” of all true statements, a correct and complete justification does not require that we enumerate every case in which it occurs. Citing just a single case is sufficient.
Take note of an important principle of reading truth tables. Completed truth tables demonstrate possibility and impossibility differently:
Truth tables demonstrate “POSSIBLE” with at least one case that you can point to with the quality under question.
Truth tables demonstrate “IMPOSSIBLE” with the absence of the quality in the entire table.
Formal Validity and Invalidity
Of course, by far the most important property that interests us occurs when the set of statements is structured as an argument. We can put arguments in a truth table by modifying how we put regular sets in a table. We’ll use commas to distinguish the premises from one another and then a single backslash to separate the conclusion from the other statements. Consider the following argument:
- ( L v B ) → H
- S ↔ L
- ~ B ∙ H
∴ ~ S
We can set this up in a single truth table to determine if the argument is valid or invalid. Our cheat sheet definitions will help us focus on what to look for in the completed table.
Validity: an argument is valid if and only if it is not possible for all the premises to be true and the conclusion false under the same conditions
Invalidity: an argument is invalid if and only if it is possible for all the premises to be true and the conclusion false under the same conditions
Here is our completed truth table for the argument:

Remember, a truth table shows impossibility when the condition is never met in the entire table. A truth table shows possibility with the condition met in just a single case.
So what do you see in this table? Do you see at least one case in which all the premises are true (i.e., under the main connectives, you see a T) and the conclusion is false (there is an F value under its main connective)? If you do see that, then you know the argument is invalid. You should then cite the case number as the justification for your judgment that the argument is invalid. If you never see this, then you make that claim as your justification.
Look again at the table to find your answer.
This argument is INVALID, case #5. We can see this clearly when we circle the case or put emphasis on it, like this:

Note that if I had seen more than one case, I would not need to cite all cases in which the premises are all true and the conclusion false. I just need to cite one case to demonstrate that it is indeed possible for this to happen. Finding many cases would not make the argument “more invalid,” so it would not strengthen my evaluation.
A Cautionary Tale
Many students new to truth tables struggle with the following observation:
I see a case in which all the statements in the argument are true!
That’s great. However, what do you think this tells you about the argument? Try this quick quiz:
T/F: An argument that has all true statements is valid.
Go ahead and take a moment to think about your answer.
We’ll wait.
Having all true statements in your argument sounds like a good thing. I mean, we are speaking the truth. Isn’t that a good thing?
Well, the answer really is: it depends.
We have to keep in mind what our intention is with what we say. If all I want to do is accurately report on the conditions of the world, then yes, having a bunch of true statements is a very good thing. However, if I want to do more with what I say, if I want to use some statements as support for the truth of another, then having all true statements is not necessarily such a resounding success. If this is my intention, then I need to judge my efforts by a higher standard than simply having the truth.
Take another look at the previous truth table. Do you see any conditions in which we have all true statements in our argument?

With the emphasis here we can easily see that, yes, case #14 depicts a situation in which all the statements are true. Cool!
Q: What does that tell you about the argument?
Q: Does this tell us if the argument is valid?
Well, look again at the truth table. Notice that case #5 is still there! The table hasn’t changed simply because we looked at case #14. The table shows that even if you are living in a world described by case #14 and all your statements are in fact true, it is still possible for all the premises to be true and the conclusion false. The possibilities for this argument are the same. Put differently, you might live in the world in which you have a bunch of true statements coming out of your mouth, but the possibility that case #5 describes for those statements isn’t going anywhere. Your argument is still invalid.
Shortened Truth Tables
We have seen how a complete truth table can help us quickly evaluate statements, sets of statements, and arguments for their formal properties. Often enough, the tables are of manageable size to set up quickly and complete without too much burden. However, once we get past four atomics, truth tables start to get a bit unwieldy in size. Doing a 32- or 64-line or larger truth table is good for the soul—it builds mental toughness. However, as a practical matter, it is very time-consuming. At the end of it all, we really end up only looking at those few lines that demonstrate the possibility of a combination of truth values that interest us. So, this is a clue as to how we can shorten up truth tables.
A shortened truth table requires a very high level of mastery over the basic conditions of truth for our logical operators. The “short” in shortened truth table makes it sound easy, and thus appealing; however, you will likely make serious errors if you are not very well-versed in the basic conditions of truth. You are likely to be more successful completing a full truth table than a shortened one until you become really familiar with how the logical operators work. Consider this a warning.
We can use shortened truth tables for most any logical property we would like to investigate. However, the most common use is to test for validity. We remember that validity is defined as a certain “impossibility” which requires an entire truth table to demonstrate. However, invalidity is defined as a certain type of “possibility” which requires only one line of a truth table. That line is as follows:
| P1 | P2 | P3 | / | C |
| T | T | T | F |
Whatever our premises and conclusion, we know that under the main connective of each must appear this specific combination of truth values to show that the argument is invalid. I don’t really care what the case number is on a truth table; I just want to know if this is a possibility. So…let’s just set them up that way, and then use our knowledge of the basic conditions of truth to see if we can make those values work out.
Consider our previous example:
- ( L v B ) → H
- S ↔ L
- ~ B ∙ H
∴ ~ S
If we lay this out as it would appear in the upper right-hand quadrant of a truth table, it looks like this:
( L v B ) → H , S ↔ L , ~ B ∙ H / ~ S
We can then put the possible combination of truth values that we want to test under each statement’s main connective. Since we’re testing for validity, it would look like this:
( L v B ) → H , S ↔ L , ~ B ∙ H / ~ S
T T T F
If this is possible, then we know the argument is invalid.
Our next step is to see if any truth values become “forced under this possibility.”
Q: Can we look at any of these values and see that some other statement “must be” a specific truth value?
We should see one immediately drop into our lap. If our conclusion is ~ S and we are testing the possibility that it is a false statement, then S must be a true statement. So we fill this in everywhere we see an S appear:
( L v B ) → H , S ↔ L , ~ B ∙ H / ~ S
T T T T F T
Notice, because the conclusion forced a value for S, we need to keep that value for all S instances in the argument. So this is why we included this in our table for the second premise.
Now we see if this new value also forces any more values. Since our second premise is a biconditional that is true, we know both sides of the biconditional must share the same truth value. We now know that the left side is true, so this forces the right side to be true (in order to keep the T value under the double arrow). Like this:
( L v B ) → H , S ↔ L , ~ B ∙ H / ~ S
T T T T T T F T
As before, we need this same value for all instances of L. The same process repeats. We look for forced truth values with each set of values that we now know “must be the case” under our test for invalidity.
Sometimes we see multiple forced values. For example, the savvy student has likely already picked up on two more forced values. The third premise is an And statement that is true. So we know that each conjunct must be true. We also know that the first premise is a conditional statement whose antecedent is itself a disjunction (L v B) which has a true conjunct (the “L”). That forces the “v” to be true as well. Before you get all eager to start dropping these values in, you might want to slow down. Doing a shortened truth table is most successful when we take each small step in its turn. Often in logic, slow is faster. Slow is also more accurate. So, let’s proceed slowly.
Remember that we just said our third premise, ( ~ B ∙ H ), is a true And statement, and this means both conjuncts must be true. Let’s do just that one for now:
( L v B ) → H , S ↔ L , ~ B ∙ H / ~ S
T T T T T T T T T F T
Don’t forget that the “H” appears twice in the premises, so once we know that it is true in the third premise we must use that value in all other appearances of the “H” in the table. So far, so good…
The savvy student has now started to see where this is going. So far, so good… That’s the worry. If we are able to fill in all the truth values for every atomic statement without any contradiction, then we will be able to go so far as to say it is indeed possible for all the premises to be true and the conclusion false. We are trying to see if these values pan out, or if we run into a situation where we cannot fill in truth values without violating our principle of bivalence (i.e., no statement can be both true and false under the same conditions). Let’s see if we can keep going.
The very savvy student has already sniffed out something quirky about our first premise. That premise is a conditional statement whose consequent is true. This means that it doesn’t matter what the truth value of the antecedent is, since the conditional will be true all the same. We also know that we really only need to see if we can give a truth value to the atomic “B” statement that is in the antecedent.
Since the truth value of the antecedent no longer matters, we are pretty confident that we can give B any truth value that may be required if one is forced upon it somewhere else in the argument. So we look for other instances of the atomic B.
Of course, we find a B in the third premise. Moreover, the value for B there is forced. Because ~ B must be a true statement, the B must be false.
( L v B ) → H , S ↔ L , ~ B ∙ H / ~ S
T F T T T T T TF T T F T
Now we can see that the truth values of all the atomics have been found without creating any contradictions. We could fill in the truth value for ( L v B ) if we wanted, but as we realized earlier, it really doesn’t matter. The little “v” is true, but the first premise was going to be true anyway. This means we have found a possible scenario in which all premises are true and the conclusion is false. Which scenario? The one in which the truth values of the atomics that define that scenario are as follows:
L B H S
T F T T
Under this case (the case # doesn’t really matter), conditions are such that all premises are true and the conclusion is false. We have demonstrated that this is possible. Thus, the argument is invalid.
So what happens when the argument is valid? In this case, we will try as we just did to fill in all combinations of truth values. However, along the way we will realize that we cannot keep going so far. We get forced into claiming that the truth value for a given statement is both true and false. That cannot be possible, thus the argument is valid (because the only way to show all true premises and a false conclusion is to insist that the statements are not “really” those truth values).
Here’s a simple example:
- Y → G
- Y
∴ G
Clearly, this is a valid argument; after all, it is nothing more than an instance of the valid form modus ponens (which we will use extensively in the next chapter). To prove that this is valid, we put it in a shortened truth table:
Y → G , Y / G
T T F
Since one of our premises is already an atomic, this forces all other instances of “Y” to share the same value. So we put that in:
Y → G , Y / G
T T T F
Of course, the same can be said of our conclusion, so that would have been a fine place to start as well. We chose the atomic Y, so let’s stick with that for a bit.
When we put the truth value in for the Y that appears in the first premise, we should see that this forces a value for the G in that premise. After all, the first premise is a true conditional statement whose antecedent is true. This means the consequent must be true in order to maintain the T under the arrow. So we put that in:
Y → G , Y / G
T T T T F
So far, so good. Now we have a truth value for Y and we have a truth value for G. But wait! We have two truth values for the atomic G! In the premise, G must be true, but in the conclusion, it is F. We would have to change the truth value in the conclusion to a T, which is conventionally shown like this:
Y → G , Y / G
T T T T F/T
Now our shortened truth table demonstrates that the only way to make these values work out is for G to have two truth values at once. This is not possible. Thus, the argument is valid. Put differently, the only way to make a case in which all premises are true and the conclusion false requires something that is not possible.
In practice, when doing shortened truth tables, there may be several ways to show that a combination of truth values is not possible. So your friend’s shortened truth table may appear different than yours, yet both tables are correct. The difference between the two will be the result of your each following up on a different forced value.
Last word on shortened truth tables: You do not have to do them.
If this all sounds like far too much thought to put into a truth table, fine. You can fill out a complete truth table without much effort; it just takes a bit of time. The full table will demonstrate the same possibility or impossibility. Full truth tables work, and they are not terribly hard to complete.
However, if you feel like you have the hang of the basic conditions of truth, shortened truth tables are kind of fun and more engaging than a full table. And yes, if we’re talking about a 128-line truth table, shortening that kind of beast up will save a bit of time too.

