3 Introduction to Principles of Inductive Reasoning—Analogy and Causality

Types of Inductive Logic

Our previous chapter helped us see that there are many ways in which informal errors can find their way into our reasoning. While this is very helpful, we should also consider positive ways in which our thinking can be sharpened. Put another way, knowing what not to do is good, but so too is knowing what we should do.

Valid reasoning is one thing we should do, and we will explore this in much greater detail later. However, valid reasoning is not the only kind of “good” reasoning. So, even when we are not striving for formally valid reasoning, the fates do not doom us to commit informal errors. We can still do a fine job thinking about things if we know some basic principles of inductive reasoning.

Back in Chapter 1, we made a distinction between deductive and inductive arguments. While deductive arguments attempt to provide premises that guarantee their conclusions, inductive arguments are less ambitious. They merely aim to provide premises that make the conclusion more probable. Because of this difference, it is inappropriate to evaluate deductive and inductive arguments by the exact same standards.

We do not use the terms “valid” and “invalid” when evaluating inductive arguments: technically, they’re all invalid because their premises don’t guarantee their conclusions, but that’s not a full and fair evaluation, since inductive arguments don’t even pretend to provide such a guarantee. Rather, we say of inductive arguments that they are strong or weak—the more probable the conclusion in light of the premises, the stronger the inductive argument; the less probable the conclusion, the weaker. These judgments can change in light of new information. Additional evidence may have the effect of making the conclusion more or less probable—of strengthening or weakening the argument.

The topic of this chapter will be inductive logic: we will be learning about the various types of inductive arguments and how to evaluate them. Inductive arguments are a rather motley bunch. They come in a wide variety of forms that can vary according to subject matter; they resist the uniform treatment we were able to provide for their deductive cousins. We will have to examine a wide variety of approaches—different inductive logics.

While all inductive arguments attempt to make their conclusions more probable, it is not always possible for us to make precise judgments about exactly how probable their conclusions are in light of their premises. When that is the case, we will make relative judgments: this argument is stronger or weaker than that argument, though I can’t say how much stronger or weaker, precisely. Sometimes, however, it will be possible to render precise judgments about the probability of conclusions, so it will be useful for us to acquire basic skills in calculating probabilities. For present purposes, this textbook will not delve into statistical analysis.

In this chapter, we will look at two very common types of inductive reasoning: arguments from analogy and inferences involving causation. The former are quite common in everyday life; the latter are the primary methods of scientific and medical research.

Each type of reasoning exhibits certain patterns, and we will look at the general forms of analogical and causal arguments; we want to develop the skill of recognizing how particular instances of reasoning fit these general patterns. We will also learn how these types of arguments are evaluated. Generally, for analogy, we will identify the criteria that we use to make relative judgments about strength and weakness. For causal reasoning, we will compare the various forms of inference to identify those most likely to produce reliable results, and we will examine some of the pitfalls peculiar to each that can lead to errors.

Arguments from Analogy

Analogical reasoning is ubiquitous in everyday life. We rely on analogies—similarities between present circumstances and those we’ve already experienced—to guide our actions. We use comparisons to familiar people, places, and things to guide our evaluations of novel ones. We criticize people’s arguments based on their resemblance to obviously absurd lines of reasoning. In this section, we will look at the various uses of analogical reasoning. Along the way, we will identify a general pattern that all arguments from analogy follow and learn how to show that particular arguments fit the pattern. We will then turn to the evaluation of analogical arguments: we will identify six criteria that govern our judgments about the relative strength of these arguments. Finally, we will look at the use of analogies to refute other arguments.

The Form of Analogical Arguments

Perhaps the most common use of analogical reasoning is to predict how the future will unfold based on similarities to past experiences. Consider this simple example. When I first learned that the movie The Wolf of Wall Street was coming out, I predicted that I would like it. My reasoning went something like this:

The Wolf of Wall Street is directed by Martin Scorsese, and it stars Leonardo DiCaprio. Those two have collaborated several times in the past, such as on Gangs of New York, The Aviator, The Departed, and Shutter Island. I liked each of those movies, so I predict that I will like The Wolf of Wall Street.

Notice, first, that this is an inductive argument. The conclusion, that I will like The Wolf of Wall Street, is not guaranteed by the premises; as a matter of fact, my prediction was wrong and I really didn’t care for the film. But our real focus here is on the fact that the prediction was made based on an analogy between The Wolf of Wall Street, on the one hand, and all the other Scorsese/DiCaprio collaborations on the other. The general pattern was something like this:

The new film is similar in important respects to the older ones; I liked all of those; so, I’ll probably like the new one.

We can use this pattern of reasoning for more overtly persuasive purposes. Consider the following:

Eating pork is immoral. Pigs are just as smart, cute, and playful as dogs and dolphins. Nobody would consider eating those animals. So why are pigs any different?

That passage is trying to convince people not to eat pork, and it does so on the basis of analogy: pigs are just like other animals we would never eat—dogs and dolphins.

Analogical arguments all share the same basic structure. We can lay out this form schematically as follows:

1. The things a1, a2, … and C all have the properties P1, P2, …
2. a1, a2, … all have property Q

So, C has Q

This is an abstract schema, and it’s going to take some getting used to, but it represents the form of analogical reasoning succinctly and clearly. Arguments from analogy can be represented as having two premises and a conclusion.

The first premise establishes an analogy. The analogy is between some thing, marked “C” in the schema, and some number of other things, marked “a1,” “a2,” and so on in the schema. We can refer to these a-things as the “analogues” while the C-thing is referred to as the “target.” Analogues are the things that are similar to the target. We say they are analogous to the target C. This schema is meant to cover every possible argument from analogy, so we do not specify a particular number of analogues; this is why we end the list with “…” to show there could be any number of them. There may be only one analogue; there may be a hundred. What’s important is that the analogues are similar to the thing designated by “C.”

What makes different things similar? They have stuff in common; they share properties. Those properties—the similarities between the analogues and C—are marked “P1,” “P2,” and so on in the diagram. Again, we don’t specify a particular number of properties shared, so we use the “…” to represent this (the number of analogues and the number of properties can of course be different). Our schema is intentionally generic: every argument from analogy fits into the framework; there may be any number of properties involved in any particular argument. Anyway, the first premise establishes the analogy: C and the analogues are similar because they have various things in common—P1, P2, P3, ….

Notice that the target “C” is missing from the second premise. The second premise only concerns the analogues: it says that they have some property in common, designated “Q” to highlight the fact that it’s not among the properties listed in the first premise. Q is a separate property; it’s the very property that we are trying to say C has in the conclusion. This is why we call C the target: we are trying to pin Q onto C, for it is the target we aim to hang it on. The thinking is something like this:

C and the analogues are similar in so many ways (first premise)

The analogues have this additional thing in common (Q in the second premise)

So, C is probably like that, too (our conclusion: C has Q).

It will be helpful to apply these abstract considerations to concrete examples. We have two in hand. The first argument, predicting that I would like The Wolf of Wall Street, fits the pattern. Here’s the argument again, for reference:

The Wolf of Wall Street is directed by Martin Scorsese, and it stars Leonardo DiCaprio. Those two have collaborated several times in the past, such as on Gangs of New York, The Aviator, The Departed, and Shutter Island. I liked each of those movies, so I predict that I will like The Wolf of Wall Street.

The conclusion is something like “I will like The Wolf of Wall Street.” Putting it that way, and looking at the general form of the conclusion of analogical arguments (C has Q), it’s tempting to say that “C” designates me, while the property Q is something like “liking The Wolf of Wall Street.” But that’s not right. The thing that “C” designates has to be involved in the analogy in the first premise; it has to be the thing that’s similar to the analogues. The analogy that this argument hinges on is between the various movies. It’s not me that “C” corresponds to; it’s the movie we’re making the prediction about. The Wolf of Wall Street is what “C” picks out.

What property are we predicting it will have? Something like “liked by me.” The analogues, a1 and so on in the schema, are the other movies: Gangs of New York, The Aviator, The Departed, and Shutter Island. These we know have the property Q (liked by me): I had already seen and liked these movies. That’s the second premise: that the analogues have Q.

Finally, the first premise, which establishes the analogy among all the movies. What do they have in common? They were all directed by Martin Scorsese, and they all starred Leonardo DiCaprio. Those are the Ps—the properties they all share. P1 is “directed by Scorsese”; P2 is “stars DiCaprio.”

The second argument we considered, about eating pork, also fits the pattern. Here it is again, for reference:

Eating pork is immoral. Pigs are just as smart, cute, and playful as dogs and dolphins. Nobody would consider eating those animals. So why are pigs any different?

Again, looking at the conclusion—”Eating pork is immoral”—and looking at the general form of conclusions for analogical arguments—C has Q—it’s tempting to just read off from the syntax of the sentence that “C” stands for “eating pork” and Q for “is immoral.” But again, that’s not right. Focus on the analogy: what things are being compared to one another? Answer: It’s the animals: pigs, dogs, and dolphins; those are our as and C. To determine which one is denoted by “C,” we ask which animal is involved in the conclusion. Answer: It’s pigs; they are denoted by “C.” So we have to paraphrase our conclusion so that it fits the form “C” has Q. Something like “Pigs shouldn’t be eaten” would work.

Q is the property “shouldn’t be eaten,” and the analogues are dogs and dolphins. They clearly have the property in question: as the argument notes, (most) everybody agrees they shouldn’t be eaten. This is the second premise.

The first premise establishes the analogy. What do pigs have in common with dogs and dolphins? Answer: They’re smart, cute, and playful. P1 = “is smart”; P2 = “is cute”; and P3 = “is playful.”

The Evaluation of Analogical Arguments

Unlike in the case of deduction, we will not have to learn special techniques to use when evaluating these sorts of arguments. It’s something we already know how to do, something we typically do automatically and unreflectively. The purpose of this section, then, is not to learn a new skill, but rather subject a familiar practice to critical scrutiny. We evaluate analogical arguments all the time without thinking about how we do it. We want to achieve a metacognitive perspective on the practice of evaluating arguments from analogy.

We want to identify the criteria that we rely on to evaluate analogical reasoning—criteria that we apply without necessarily realizing that we’re applying them. Achieving such metacognitive awareness is useful insofar as it makes us more self-aware, critical, and therefore effective reasoners.

Analogical arguments are inductive arguments. They give us reasons that are supposed to make their conclusions more probable. How probable, exactly? That’s very hard to say. How probable was it that I would like The Wolf of Wall Street given that I had liked the other four Scorsese/DiCaprio collaborations? I don’t know. How probable is it that it’s wrong to eat pork, given that it’s wrong to eat dogs and dolphins? I really don’t know. It’s hard to imagine how you would even begin to answer that question.

As we mentioned, while it’s often impossible to evaluate inductive arguments by giving a precise probability of its conclusion, it is possible to make relative judgments about strength and weakness. Recall, new information can change the probability of the conclusion of an inductive argument. We can make relative judgments like this:

If we add this new information as a premise, the new argument is stronger/weaker than the old argument; that is, the new information makes the conclusion more/less likely.

It is these types of relative judgments that we make when we evaluate analogical reasoning. We compare different arguments—with the difference being new information in the form of an added premise, or a different conclusion supported by the same premises—and judge one to be stronger or weaker than the other. Subjecting this practice to critical scrutiny, we can identify six criteria that we use to make such judgments.

We’re going to be making relative judgments, so we need a baseline argument against which to compare others. Here is such an argument:

Alice has taken four philosophy courses during her time in college. She got an A in all four. She has signed up to take another philosophy course this semester. I predict she will get an A in that course, too.

This is a simple argument from analogy, in which the future is predicted based on past experience. It fits the schema for analogical arguments: the new course she has signed up for is designated by “C”; the property we’re predicting it has (Q) is that it is a course Alice will get an A in; the analogues are the four previous courses she’s taken; what they have in common with the new course (P1) is that they are also philosophy classes; and they all have the property Q—Alice got an A in each.

Anyway, how strong is the baseline argument? How probable is its conclusion in light of its premises? I have no idea. It doesn’t matter. We’re now going to consider tweaks to the argument, and the effect that those will have on the probability of the conclusion. That is, we’re going to consider slightly different arguments, with either new information added to the original premises or changes made to the prediction, and ask whether these altered new arguments are stronger or weaker than the baseline argument. This will reveal the six criteria that we use to make such judgments. We’ll consider one criterion at a time.

1st Criteria: Number of Analogues

Suppose we alter the original argument by changing the number of prior philosophy courses Alice has taken. Instead of Alice having taken four philosophy courses before, we’ll now suppose she has taken 14. We’ll keep everything else about the argument the same: she got an A in all of them, and we’re predicting she’ll get an A in the new one. Are we more or less confident in the conclusion—the prediction of an A—with the altered premise? Is this new argument stronger or weaker than the baseline argument? Answer: It’s stronger!

We’ve got Alice getting an A 14 times in a row instead of only four. That clearly makes the conclusion more probable. (How much more? Again, it doesn’t matter.) What we did in this case is add more analogues. This reveals a general rule:

Other things being equal, the more analogues in an analogical argument, the stronger the argument (and conversely, the fewer analogues, the weaker).

The number of analogues is one of the criteria we use to evaluate arguments from analogy.

2nd Criteria: Variety of Analogues

You’ll notice that the original argument doesn’t give us much information about the four courses Alice succeeded in previously and the new course she’s about to take. All we know is that they’re all philosophy courses. Suppose we tweak things. We’re still in the dark about the new course Alice is about to take, but we know a bit more about the other four: one was a course in ancient Greek philosophy; one was a course on contemporary ethical theories; one was a course in formal logic; and the last one was a course on the philosophy of mind. Given this new information, are we more or less confident that she will succeed in the new course, whose topic is unknown to us? Is the argument stronger or weaker than the baseline argument? Answer: It is stronger. We don’t know what kind of philosophy course Alice is about to take, but this new information gives us an indication that it doesn’t really matter. She was able to succeed in a wide variety of courses, from mind to logic, from ancient Greek to contemporary ethics. This is evidence that Alice is good at philosophy generally, so that no matter what kind of course she’s about to take, she’ll probably do well in it. Again, this points to a general principle about how we evaluate analogical arguments:

Other things being equal, the more variety there is among the analogues, the stronger the argument (and conversely, the less variety, the weaker).

3rd Criteria: Number of Similarities

In the baseline argument, the only thing the four previous courses and the new course have in common is that they’re philosophy classes. Suppose we change that. Our newly tweaked argument predicts that Alice will get an A in the new course, which, like the four she succeeded in before, is cross-listed in the Department of Religious Studies and covers topics related to the philosophy of religion. Given this new information—that the new course and the four older courses were similar in ways we weren’t aware of—are we more or less confident in the prediction that Alice will get another A? Is the argument stronger or weaker than the baseline argument? Answer: Again, it is stronger. Unlike the last example, this tweak gives us new information both about the four previous courses and the new one. The upshot of that information is that the courses are more similar than we knew; that is, they have more properties in common. To P1 = “is a philosophy course,” we can add P2 = “is cross-listed with religious studies” and P3 = “covers topics in philosophy of religion.” The more properties things have in common, the stronger the analogy between them. The stronger the analogy, the stronger the argument based on that analogy. We now know not just that Alice did well in not just in philosophy classes, but specifically in classes covering the philosophy of religion, and we know that the new class she’s taking is also about the philosophy of religion. I’m much more confident predicting she’ll do well again than I was when all I knew was that all the classes were philosophy; the new one could’ve been in a different topic that she wouldn’t have liked. General principle:

Other things being equal, the more properties involved in the analogy—the more similarities between the item in the conclusion and the analogues—the stronger the argument (and conversely, the fewer properties, the weaker).

4th Criteria: Number of Differences

An argument from analogy is built on the foundation of the similarities between the analogues and the target item in the conclusion—the analogy. Anything that weakens that foundation weakens the argument. So, to the extent that there are differences among those items, the argument is weaker.

Suppose we add new information to our baseline argument: the four philosophy courses Alice did well in before were all courses on the philosophy of mind; the new course is about the history of ancient Greek philosophy. Given this new information, are we more or less confident that she will succeed in the new course? Is the argument stronger or weaker than the baseline argument? Answer: Clearly, the argument is weaker. The new course is on a completely different topic than the other ones. She did well in four straight philosophy of mind courses, but ancient Greek philosophy is quite different. I’m less confident that she’ll get an A than I was before. If I add more differences, the argument gets even weaker. Supposing the four philosophy of mind courses were all taught by the same professor (the person in the department whose expertise is in that area), but the ancient Greek philosophy course is taught by someone different (the department’s specialist in that topic). Different subject matter, different teachers: I’m even less optimistic about Alice’s continued success. Generally speaking,

Other things being equal, the more differences there are between the analogues and the item in the conclusion, the weaker the argument from analogy.

5th Criteria: Relevance of Similarities and Differences

Not all similarities and differences are capable of strengthening or weakening an argument from analogy, however. Suppose we tweak the original argument by adding the new information that the new course and the four previous courses all have their weekly meetings in the same campus building. This is an additional property that the courses have in common, which, as we just saw, other things being equal, should strengthen the argument. But other things are not equal in this case. That’s because it’s very hard to imagine how the location of the classroom would have anything to do with the prediction we’re making—that Alice will get an A in the course. Classroom location is simply not relevant to success in a course. Therefore, this new information does not strengthen the argument. Nor does it weaken it; I’m not inclined to doubt that Alice will do well considering the information about location. It simply has no effect at all on my appraisal of her chances. Similarly, if we tweak the original argument to add a difference between the new class and the other four—for example, that all four previous classes were in the same building, while the new one is in a different building—there is no effect on our confidence in the conclusion. Again, the building in which a class meets is generally not relevant to how well someone does.

Contrast these cases with the new information that the new course and the previous four are all taught by the same professor. Now that strengthens the argument! Alice has gotten an A four times in a row from this professor—all the more reason to expect she’ll receive another one. This tidbit strengthens the argument because the new similarity—the same person teaches all the courses—is relevant to the prediction we’re making—that Alice will do well. Who teaches a class can make a difference to how students do—either because they’re easy graders, or because they’re great teachers, or because the student and the teacher are in tune with one another, etc. Even a difference between the analogues and the item in the conclusion, with the right kind of relevance, can strengthen an argument. Suppose the other four philosophy classes were taught by the same teacher, but the new one is taught by a TA—who just happens to be her boyfriend. That’s a difference, but one that makes the conclusion—that Alice will do well—more probable. However, in such a case, we are more apt to treat this as an additional “stand-alone” premise, one without real influence on the strength or weakness of the analogy. Generally speaking,

Careful attention must be paid to the relevance of any similarities and differences to the property in the conclusion; the effect on strength varies.

6th Criteria: Modesty/Ambition of the Conclusion

Suppose we leave everything about the premises in the original baseline argument the same: four philosophy classes, an A in each, new philosophy class. Instead of adding to that part of the argument, we’ll tweak the conclusion:

Instead of predicting that Alice will get an A in the class, we’ll predict that she’ll simply pass the course.

Are we more or less confident that this prediction will come true? Is the new, tweaked argument stronger or weaker than the baseline argument? Answer: It’s stronger. We are more confident in the prediction that Alice will pass than we are in the prediction that she will get another A, for the simple reason that it’s much easier to pass than it is to get an A. That is, the prediction of passing is a much more modest prediction than the prediction of an A.

Suppose we tweak the conclusion in the opposite direction—not more modest, but more ambitious. Alice has gotten an A in four straight philosophy classes. She’s about to take another one, and I predict that she will do so well that her professor will suggest that she publish her term paper in one of the most prestigious philosophical journals, and that she will be offered a three-year research fellowship at the Institute for Advanced Study at Princeton University. That’s a bold prediction! Meaning, of course, that it’s very unlikely to happen. Getting an A is one thing; getting an invitation to be a visiting scholar at one of the most prestigious academic institutions in the world is quite another. The argument with this ambitious conclusion is weaker than the baseline argument. General principle:

The more modest the argument’s conclusion, the stronger the argument; the more ambitious, the weaker.

Refutation by Analogy

We can use arguments from analogy for a specific logical task: refuting someone else’s argument, showing that we are not compelled to accept the conclusion. Recall the case of deductive arguments. To refute those meant showing they are invalid—we had to produce a counterexample. This meant providing a new argument with the same logical form as the original, the same pattern of syntax found in the premises and conclusion. However, this new argument needed to be obviously invalid, in that its premises were in fact true and its conclusion in fact false.

We can use a similar procedure to refute inductive arguments. Of course, the standard of evaluation is different for induction: we don’t judge them according to the black and white standard of validity. And as a result, our judgments have less to do with form than with content. Nevertheless, refutation along similar lines is possible, and analogies are the key to the technique.

To refute an inductive argument, we produce a new argument that’s obviously bad—just as we did in the case of deduction. We don’t have a precise notion of logical form for inductive arguments, so we can’t demand that the refuting argument have the same syntax as the original; rather, we want the new argument to have an analogous form of reasoning to the original. The stronger the analogy between the refuting and refuted arguments, the more decisive the refutation. We cannot produce the kind of knock-down refutations that were possible in the case of deductive arguments, where the standard of evaluation—validity—does not admit of degrees of goodness or badness, but the technique can be quite effective.

Consider the following scenario:

You and your friend are watching TV. A news story reports that Duck Dynasty star Willie Robertson said he supports Trump because both of them have been successful businessmen and stars of reality TV shows. Your friend scoffs and says:

By that logic, does that mean Hugh Hefner’s success with Playboy and his occasional appearances on Bad Girls Club warrant him as a worthy president?

Your friend is refuting the argument of Willie Robertson, the Duck Dynasty star. Robertson’s argument is something like this:

Trump is a successful businessman and reality TV star.

Therefore, he would be a good president.

To refute this, your friend makes an analogy between Trump and Hugh Hefner. Your friend uses this to produce an analogous argument:

Hugh Hefner is a successful businessman and reality TV star.

Therefore, Hugh Hefner would make a good president

This is regarded by your friend as obviously bad.

Therefore, the original argument about Trump is just as obviously bad.

What makes it obviously bad is that it has a conclusion that nobody would agree with; nobody is likely to believe that Hugh Hefner would make a good president. That’s how these refutations work. They attempt to demonstrate that the original argument is lousy by showing that you can use the same or very similar reasoning to arrive at an absurd conclusion. That is, they use an analogy between the two attempts at reasoning to demonstrate the flaw in the original argument (which is the target we want to pin “bad reasoning” onto).

Here’s another example, from a group called “Iowans for Public Education,” who wanted to support funding for public schools by showing flaws in the views of people who want to use those funds for private schooling options.

Next to a picture of a seemingly wealthy lady is the following text:

“My husband and I have decided the local parks just aren’t good enough for our kids. We’d rather use the country club, and we are hoping state tax dollars will pay for it. We are advocating for Park Savings Accounts, or PSAs. We promise to no longer use the local parks. To hell with anyone else or the community as a whole. We want our tax dollars to be used to make the best choice for our family.”

Sound ridiculous? Tell your legislator to vote NO on Education Savings Accounts (ESAs), a.k.a. school vouchers.

The argument that Iowans for Public Education put in the mouth of the lady on the poster is meant to refute reasoning used by advocates for “school choice.” Those advocates say that they ought to have the right to opt out of public education and keep the tax dollars they would otherwise pay for public schools to pay for their kids to attend private schools. A similar line of reasoning sounds pretty crazy when you replace “public schools” with “public parks,” “private schools” with “country clubs,” and “ESAs” with “PSAs.” The argument from analogy works here because our judgment of the line of reasoning in the parks argument is now attached to the target: the reasoning offered in the school-choice arguments.

Since these sorts of refutations rely on analogies, they are only as strong as the analogy between the refuting and refuted arguments. There is room for dispute on that question. Advocates for school vouchers might point out that schools and parks are completely different things, that schools are much more important to the future prospects of children, and that given the importance of education, families should have the right to choose what they think is best. Or something like that. The point is, when attacked by an argument from analogy, those defending their position will need to undermine the strength of the analogy. Their strategy will be to chip away at the alleged similarities between analogue and target. Those pushing for the analogy will try to counter-respond by maintaining enough of the criteria for evaluating arguments from analogy (e.g., Number Analogues, Relevance of Similarities, etc.). This is always a complex affair. The kinds of knock-down refutations that were possible for deductive arguments are not possible for inductive arguments.

Exercises

1. Show how the following arguments fit the abstract schema for arguments from analogy:

a1, a2, …, and C all have P1, P2, …

a1, a2, …, all have Q ___________________

So C has Q

1. 1. You should really eat at Papa Giorgio’s; you’ll love it. It’s just like Mama DiSilvio’s and Matteo’s, which I know you love: they serve old-fashioned Italian-American food, they have a laid-back atmosphere, and the wine list is extensive.
   2. George R.R. Martin deserves to rank among the greats in the fantasy literature genre. Like C.S. Lewis and J.R.R. Tolkien before him, he has created a richly detailed world, populated it with compelling characters, and told a tale that is not only exciting, but which features universal and timeless themes concerning human nature.
   3. Yes, African Americans are incarcerated at higher rates than whites. But blaming this on systemic racial bias in the criminal justice system is absurd. That’s like saying the NBA is racist because there are more black players than white players, or claiming that the medical establishment is racist because African Americans die young more often.

2. Consider the following baseline argument:

I’ve taken vacations to Florida six times before, and I’ve enjoyed each visit. I’m planning to go to Florida again this year, and I fully expect yet another enjoyable vacation.

For each of the following changes:

1. 1. Decide which produces an argument that’s weaker or stronger than the baseline argument
      and
   2. Indicate which of the six criteria for evaluating analogical arguments justifies that judgment

3. For each of the following passages, explicate the argument being refuted and the argument or arguments doing the refuting.

1. 1. Republicans tell us that, because at some point 40 years from now a shortfall in revenue for Social Security is projected, we should cut benefits now. Cut them now because we might have to cut them in the future? I’ve got a medium-sized tree in my yard. 40 years from now, it may grow so large that its branches hang over my roof. Should I chop it down?
   2. Opponents of gay marriage tell us that it flies in the face of a tradition going back millennia: that marriage is between a man and a woman. There were lots of traditions that lasted a long time: the tradition that it was OK for some people to own other people as slaves, the tradition that women couldn’t participate in the electoral process—the list goes on. That it’s traditional doesn’t make it right.
   3. Some people claim that their children should be exempted from getting vaccinated for common diseases because the practice conflicts with their religious beliefs. But religion can’t be used to justify just anything. If a Satanist tried to defend himself against charges of abusing children by claiming that such practices were a form of religious expression, would we let him get away with it?

Causal Reasoning

Inductive arguments are frequently used to support claims about cause and effect. These arguments come in a number of different forms. The most straightforward is what is called enumerative induction. This is an argument that makes a (non-hasty) generalization, inferring that one event or type of event causes another on the basis of a (large) number of particular observations of the cause immediately preceding the effect. To use a very famous example (from the history of philosophy, per David Hume, the 18th century Scottish philosopher), we can infer from observations of a number of billiard ball collisions that the first ball colliding with the second causes the second ball to move.

This is all well and good, so far as it goes. It just doesn’t go very far. If we want to establish a robust knowledge of what causes the natural phenomena we’re interested in, we need techniques that are more sophisticated than simple enumerative induction. Fortunately, there are such techniques. These are patterns of reasoning identified and catalogued by the 19th century English philosopher John Stuart Mill. The inferential forms Mill enumerated have come to be called “Mill’s Methods,” because he thought of them as tools to be used in the investigation of nature—methods of discovering the causes of natural phenomena. In this section, we will look at Mill’s Methods each in turn (there are five of them), using examples to illustrate each. We will finish with a discussion of the limitations of the methods and the difficulty of isolating causes.

The Meaning(s) of “Cause”

Before we proceed, however, we must issue something of a disclaimer: when we say that one action or event causes another, we don’t really know what the hell we’re talking about. OK, maybe that’s putting it a bit too strongly. The point is this: the meaning of “cause” has been the subject of intense philosophical debate since ancient times (in both Greece and India)—debate that continues to this day. Myriad philosophical theories have been put forth over the millennia about the nature of causation, and there is no general agreement about just what it is (or whether causes are even real!).

We’re not going to wade into those philosophical waters; they’re too deep. Instead, we’ll merely dip our toes in, by making a preliminary observation about the word “cause”—an observation that gives some hint as to why it’s been the subject of so much philosophical deliberation for so long. The observation is this:

There are a number of distinct, but perfectly acceptable, ways that we use the word “cause” in everyday language. We attach different incompatible meanings to the term in different contexts.

Consider this scenario: I’m in my backyard vegetable garden with my younger daughter (age four at the time). She’s “helping” me in my labors by watering some of the plants. She asks, “Daddy, why do we have to water the plants?” I might reply, “We do that because water causes the plants to grow.” This is a perfectly ordinary claim about cause and effect; it is uncontroversial and true. What do I mean by “causes” in this sentence? I mean that water is a necessary condition for the plants to grow. Without water, there will be no growth. It is not a sufficient condition for plant growth, though: you also need sunlight, good soil, etc.

Consider another completely ordinary, uncontroversial truth about causation: decapitation causes death. What do I mean by “causes” in this sentence? I mean that decapitation is a sufficient condition for death. If death is the result you’re after, decapitation will do the trick on its own; nothing else is needed. It is not (thank goodness) a necessary condition for death, however. There are lots of other ways to die besides beheading.

Finally, consider this true claim: smoking causes cancer. What do I mean by “causes” in this sentence? Well, I don’t mean that smoking is a sufficient condition for cancer. Lots of people smoke all their lives but are lucky enough not to get cancer. Moreover, I don’t mean that smoking is a necessary condition for cancer. Lots of people get cancer—even lung cancer—despite having never smoked. Rather, what I mean is that smoking tends to produce cancer; it increases the probability that one will get cancer.

So, we have three totally ordinary uses of the word “cause,” with three completely different meanings: cause as necessary condition, sufficient condition, and mere tendency (neither necessary nor sufficient). These are incompatible, but all acceptable in their contexts. We could go on to list even more uses for the term, but the point has been made. Causation is a slippery concept, which is why philosophers have been struggling for so long to capture its precise meaning. In what follows, we will set aside these concerns and speak about cause and effect without hedging or disclaimers, but it’s useful to keep in mind that doing so papers over some deep and difficult philosophical problems.

Mill’s Methods

John Stuart Mill identified five different patterns of reasoning that one could use to discover causes. These are argument forms, the conclusions of which involve a claim to the effect that one thing causes (or is causally related to) another. They can be used alone or in combination, depending on the circumstances.

As was the case with analogical reasoning, these are patterns of inference that we already employ unreflectively in everyday life. The benefit of making them explicit and subjecting them to critical scrutiny is that we thereby achieve a metacognitive perspective—a perspective from which we can become more self-aware, effective reasoners. This is especially important in the context of causal reasoning, since, as we shall see, there are many pitfalls in this domain that we are prone to fall into, many common errors that people make when thinking about cause and effect.

Method of Agreement

We could sum up this reasoning pattern abstractly thus: We want to find the cause of a phenomenon: call it X. We examine a variety of circumstances in which X occurs, looking for potential causes. The circumstances differ in various ways, but they each have in common that they feature the same potential cause: call it A. We conclude that A causes X. Each of the circumstances agrees with the others in the sense that they all feature the same potential cause—hence, the Method of Agreement. Consider the following story:

I’ve been suffering from heartburn recently. Seems like at least two or three days a week, by about dinnertime, I’ve got that horrible feeling of indigestion in my chest and that yucky taste in my mouth. Acid reflux: ugh. I’ve got to do something about this. What could be causing my heartburn, I wonder? I know that the things you eat and drink are typical causes of the condition, so I start thinking back, looking at what I’ve consumed on the days when I felt bad. As I recall, all of the recent days on which I suffered heartburn were different in various ways: my dinners ranged from falafel to spaghetti to spicy burritos; sometimes I had a big lunch, sometimes very little; on some days I drank a lot of coffee at breakfast, but other days not any at all. But now that I think about it, one thing stands out: I’ve been in a nostalgic mood lately, thinking about the good old days when I was a carefree college student. I’ve been listening to lots of music from that time, watching old movies, etc. And as part of that trip down memory lane, I’ve re-acquired a taste for one of my favorite beverages from that era—Mountain Dew. I’ve been treating myself to a nice bottle of the stuff with lunch now and again. And sure enough, each of the days that I got heartburn was a day when I drank Mountain Dew at lunch. Huh. I guess the Mountain Dew is causing my heartburn. I better stop drinking it.

This little story is an instance of Mill’s Method of Agreement. It’s a pattern of reasoning that one can use to figure out the cause of some phenomenon of interest. In this case, the phenomenon I want to discover the cause of is my recent episodes of heartburn. I eventually figure out that the cause is Mountain Dew. Though the circumstances of my heartburn varied in many ways, consuming Mountain Dew was the common feature in each instance of heartburn. So, I conclude that it causes my heartburn.

In the story above, the phenomenon X that I wanted to find the cause of was heartburn; the various circumstances were the days on which I had suffered that condition, and they varied with respect to potential causes (foods and beverages consumed); however, they all agreed in featuring Mountain Dew, which is the factor A causing the heartburn, X.

More simply, we can sum up the Method of Agreement as a simple question:

In the case of our little story, Mountain Dew was present whenever heartburn was present, so we concluded that it was the cause.

Method of Difference

We can sum up this pattern of reasoning abstractly thus: We want to find the cause of a phenomenon: call it X. We examine a variety of circumstances in which X occurs, looking for potential causes. The circumstances differ in various ways, but they each have in common that when we remove from them a potential cause—call it A—the phenomenon disappears. We conclude that A causes X. If we introduce the same difference in all of the circumstances—removing the causal factor—we see the same effect—disappearance of the phenomenon. Hence, the Method of Difference. Consider the following story:

Everybody in my house has a rash! Itchy skin, little red bumps; it’s annoying. It’s not just the grownups—me and my wife—but the kids, too. Even the dog has been scratching herself constantly! What could possibly be causing our discomfort? My wife and I brainstorm, and she remembers that she recently changed brands of laundry detergent. Maybe that’s it. So we re-wash all the laundry (including the pillow that the dog sleeps on in the windowsill) in the old detergent and wait. Sure enough, within a day or two, everybody’s rash is gone. Sweet relief!

This story presents an instance of Mill’s Method of Difference. Again, we use this pattern of reasoning to discover the cause of some phenomenon that interests us—in this case, the rash we all have. We end up discovering that the cause is the new laundry detergent. We isolated this cause by removing that factor and seeing what happened.

In our story, the phenomenon we wanted to explain, X, was the rash. The varying circumstances are the different inhabitants of my house—Mom, Dad, kids, even the dog—and the different factors affecting them. The factor that we removed from each, A, was the new laundry detergent. When we did that, the rash went away, so the detergent was the cause of the rash—A caused X.

More simply, we can sum up the Method of Difference as a simple question:

In the case of our little story, when the detergent was absent, so too was the rash. We concluded that the detergent caused the rash.

Joint Method of Agreement and Difference

This isn’t really a new method at all. It’s just a combination of the first two. The Methods of Agreement and Difference are complementary; each can serve as a check on the other. Using them in combination is an extremely effective way to isolate causes.

The Joint Method is an important tool in many forms of research. It’s the pattern of reasoning used in what we call controlled studies. In such a study, we split our subjects into two groups to verify casual claims. An example shows how this works. Suppose I’ve formulated a pill that I think is a miracle cure for baldness. I’m gonna be rich! But first, I need to see if it really works. So I gather a bunch of bald men together for a controlled study. One group gets the actual drug; the other, the control group, gets a sugar pill—not the real drug at all, but a mere placebo, a “fake” pill that we know won’t have any causal influence on the test subjects. Then I wait and see what happens. If my drug is a good as I think it is, two things will happen: first, the group that got the drug will grow new hair; second, the group that got the placebo won’t grow new hair. If either of these things fails to happen, it’s back to the drawing board. Obviously, if the group that got the drug didn’t get any new hair, my baldness cure is a dud. But in addition, if the group that got the mere placebo grew new hair, then something else besides my drug has to be the cause. In this way we rule out a false positive result that we would have gotten if I only had one group of men take my new pill and they saw their hair growth improve—it would falsely look like my pill was the cause of that new hair growth.

Both the Method of Agreement and the Method of Difference are being used in a controlled study. I’m using the Method of Agreement on the group that got the drug. I’m hoping that whenever the causal factor (my miracle pill) is present, so too will be the phenomenon of interest (hair growth). The control group complements this with the Method of Difference. For them, I’m hoping that whenever the causal factor (the miracle pill) is absent, so too will be the phenomenon of interest (hair growth). If both things happen, I’ve got strong confirmation that my drug causes hair growth.

Method of Residues

“Residue” in this context just means the remainder, that which is left over. This pattern of reasoning, put abstractly, runs something like this: We observe a series of phenomena, call them X1, X2, X3, …, Xn. As a matter of background knowledge, we know that X1 is caused by A1, that X2 is caused by A2, and so on. But when we exhaust our background knowledge of the causes of phenomena, we’re left with one, Xn, that is inexplicable in those terms. So, we must seek out an additional causal factor, An, as the cause of Xn. The leftover phenomenon, Xn, inexplicable in terms of our background knowledge, is the residue. Consider the following story. You may not be familiar with all the terminology, but just pay close attention to the numbers and see how they add up…

I’m running a business. Let’s call it LogiCorp. For a modest fee, the highly trained logicians at LogiCorp will evaluate all of your deductive arguments, issuing Certificates of Validity (or Invalidity) that are legally binding in all fifty states. Satisfaction guaranteed. Anyway, as should be obvious from that brief description of the business model, LogiCorp is a highly profitable enterprise. But last year’s results were disappointing. Profits were down 20% from the year before.

Some of this was expected. We undertook a renovation of the LogiCorp World Headquarters that year, and the cost had an effect on our bottom line: half of the lost profits, 10%, can be chalked up to the renovation expenses. Also, as healthcare costs continue to rise, we had to spend additional money on our employees’ benefits packages; these expenditures account for an additional 3% of profit shortfall. Finally, another portion of the drop in profits can be explained by the entry of a competitor into the marketplace. The upstart firm Arguments R Us, with its fast turnaround times and ultra-cheap prices, has been cutting into our market share. Their services are totally inferior to ours (you should see the shoddy shading technique in their Venn diagrams!) and LogiCorp will crush them eventually, but for now they’re hurting our business: competition from Arguments R Us accounts for a 5% drop in our profits.

As CEO, I was of course aware of all these potential problems throughout the year, so when I looked at the numbers at the end, I wasn’t surprised. But when I added up the contributions from the three factors I knew about—10% from the renovation, 3% from the healthcare expenditures, 5% from outside competition—I came up short. Those causes only account for an 18% shortfall in profit, but we were down 20% on the year; there was an extra 2% shortfall that I couldn’t explain.

I’m a suspicious guy, so I hired an outside security firm to monitor the activities of various highly placed employees at my firm. And I’m glad I did! Turns out my Chief Financial Officer had been taking lavish weekend vacations to Las Vegas and charging his expenses to the company credit card. His thievery surely accounts for the extra 2%. I immediately fired the jerk.

This little story presents an instance of Mill’s Method of Residues. In our story, that was the additional 2% profit shortfall that couldn’t be explained in terms of the causal factors we were already aware of, namely the headquarters renovation (A1, which caused X1, a 10% shortfall), the healthcare expenses (A2, which caused X2, a 3% shortfall), and the competition from Arguments R Us (A3, which caused X3, a 5% shortfall). We had to search for another, previously unknown cause for the final, residual 2%.

Method of Concomitant Variation

Put abstractly, this pattern of reasoning goes something like this: We observe that, holding other factors constant, an increase or decrease in some causal factor A is always accompanied by a corresponding increase or decrease in some phenomenon X. We conclude that A and X are causally related.

Things that “vary concomitantly” are things, to put it more simply, that change together. As A changes—goes up or down—X changes, too. There are two ways things can vary concomitantly: directly or inversely. If A and X vary directly, that means that an increase in one will be accompanied by an increase in the other (and a decrease in one will be accompanied by a decrease in the other); if A and X vary inversely, that means an increase in one will be accompanied by a decrease in the other.

Fact: if you’re a person who currently maintains a fairly steady weight, and you change nothing else about your lifestyle, adding 500 calories per day to your diet will cause you to gain weight. Conversely, if you cut 500 calories per day from your diet, you will lose weight. That is, calorie consumption and weight are causally related: consuming more will cause weight gain; consuming less will cause weight loss.

Another fact: if you’re a person who currently maintains a steady weight, and you change nothing else about your lifestyle, adding an hour of vigorous exercise per day to your routine will cause you to lose weight. Conversely (assuming you already exercise a heck of a lot), cutting that amount of exercise from your routine will cause you to gain weight. That is, exercise and weight are causally related: exercising more will cause weight loss; exercising less will cause weight gain.

I know about the cause-and-effect relationships above because of the Method of Concomitant Variation. In our first example, calorie consumption (A) and weight (X) vary directly. As calorie consumption increases, weight increases; as calorie consumption decreases, weight decreases. In our second example, exercise (A) and weight (X) vary inversely. As exercise increases, weight decreases; as exercise decreases, weight increases. Either way, when things change together in this way, when they vary concomitantly, we conclude that they are causally related.

The Difficulty of Isolating Causes

Mill’s Methods are useful in discovering the causes of phenomena in the world, but their usefulness should not be overstated. Unless they are employed thoughtfully, they can lead an investigator astray.

A classic example of this is the parable of the drunken logician.^[1] After a long day at work on a Monday, a certain logician heads home wanting to unwind. So he mixes himself a “7 and 7”—Seagram’s 7 Crown whiskey and 7-Up. It tastes so good, he makes another—and another, and another. He drinks seven of these cocktails, passes out in his clothes, and wakes up feeling terrible (headache, nausea, etc.). On Tuesday, after dragging himself into work, toughing it through the day, then finally getting home, he decides to take the edge off with a different drink: brandy and 7-Up. He gets carried away again, and ends up drinking seven of these cocktails, with the same result: passing out in his clothes and waking up feeling awful on Wednesday. So, on Wednesday night, our logician decides to mix things up again: scotch and 7-Up. He drinks seven of these: same results. But he perseveres! Thursday night, it’s seven vodka and 7-Ups; another blistering hangover on Friday. So on Friday at work, he sits down to figure out what’s going on.

He’s got a phenomenon—hangover symptoms every morning of that week—that he wants to discover the cause of. He’s a professional logician, intimately familiar with Mill’s Methods, so he figures he ought to be able to discover the cause. He looks back at the week and uses the Method of Agreement, asking, “What factor was present every time the phenomenon was?” He concludes that the cause of his hangovers is 7-Up.

Our drunken logician applied the Method of Agreement correctly: 7-Up was indeed present every time. But it clearly wasn’t the cause of his hangovers. The lesson is that Mill’s Methods are useful tools for discovering causes, but their results are not always definitive. Uncritical application of the methods can lead one astray. Additional knowledge must often be brought to bear on our conclusions (e.g., knowledge of the alcohol content of 7-Up would have probably helped our logician avoid his error). Critical evaluation of a hypothesis requires more than the sole application of Mill’s Methods.

This is especially true of the Method of Concomitant Variation. You may have heard the old saw that “correlation does not imply causation.” It’s useful to keep this corrective in mind when using the Method of Concomitant Variation. That two things vary concomitantly is a hint that they may be causally related, but it is not definitive proof that they are. They may be separate effects of a different, unknown cause; they may be completely causally unrelated.

It is true, for example, that among children, shoe size and reading ability vary directly: children with bigger feet are better readers than those with smaller feet. Wow! So large feet cause better reading? Of course not. Larger feet and better reading ability are both effects of the same cause: getting older. Older kids wear bigger shoes than younger kids, and they also do better on reading tests. Duh.

It is also true, for example, that hospital quality and death rate vary directly: that is, the higher quality the hospital (prestige of doctors, training of staff, sophistication of equipment, etc.), on average, the higher the death rate at that hospital. That’s counterintuitive! Does that mean that high hospital quality causes high death rates? Of course not. Better hospitals have higher mortality rates because the extremely sick, most badly injured patients are taken to those hospitals, rather than to the ones with lower-quality staff and equipment. Alas, these people die more often, but not because they’re at a good hospital; it’s exactly the reverse.

Spurious correlations—those that don’t involve any causal connection at all—are easy to find in the age of “big data.” With publicly available databases archiving large amounts of data, and computers with the processing power to search them and look for correlations, it is possible to find many examples of phenomena that vary concomitantly but are obviously not causally connected.

A very clever person named Tyler Vigen set about doing this and created a website where he posted his (often very amusing) discoveries.^[2] For example, he found that between 2000 and 2009, per capita cheese consumption among Americans was very closely correlated with the number of deaths caused by people becoming entangled in their bedsheets.

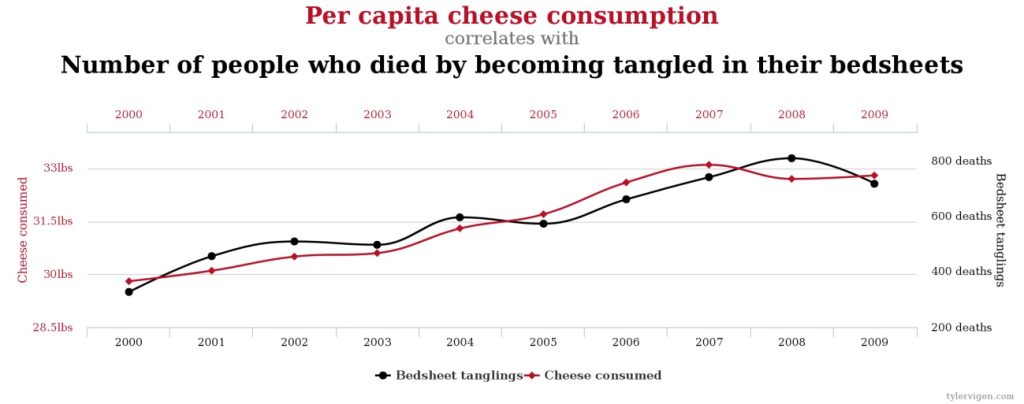
These two phenomena vary directly, but it’s hard to imagine how they could be causally related. It’s even more difficult to imagine how the following two phenomena could be causally related:

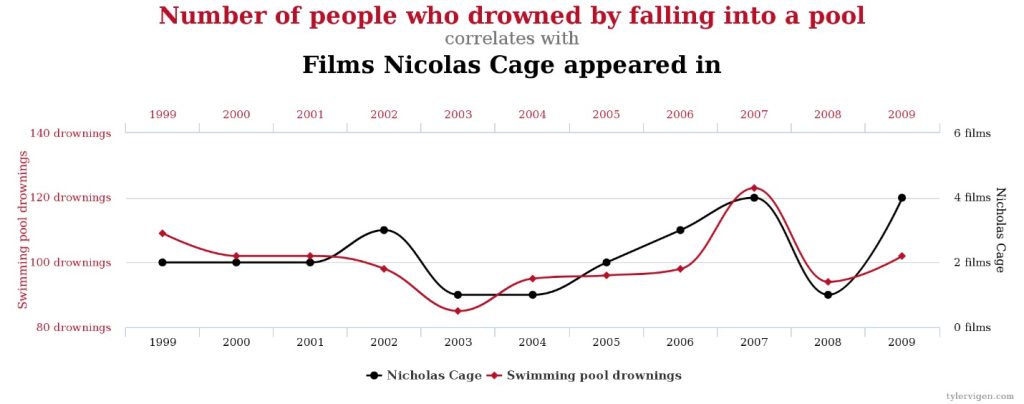
So, Mill’s Methods can’t just be applied willy-nilly; one could end up “discovering” causal connections where none exist. They can provide clues as to potential causal relationships, but care and critical analysis are required to confirm those results. It’s important to keep in mind that the various methods can work in concert, providing a check on each other. If the drunken logician, for example, had applied the Method of Difference—removing the 7-Up but keeping everything else the same—he would have discovered his error (he would’ve kept getting hangovers). The combination of the Methods of Agreement and Difference—the Joint Method, the controlled study—is an invaluable tool in modern scientific research. A properly conducted controlled study can provide quite convincing evidence of causal connections (or a lack thereof).

Of course, properly conducting a controlled study is not as easy as it sounds. It involves more than just the application of the Joint Method of Agreement and Difference. There are other potentially confounding factors that must be accounted for in order for such a study to yield reliable results. For example, it’s important to take great care in separating subjects into the test and control groups: there can be no systematic difference between the two groups other than the factor that we’re testing; if there is, we cannot say whether the factor we’re testing or the difference between the groups is the cause of any effects observed.

Suppose we were conducting a study to test the common belief that vitamin C is effective in treating the common cold. We gather 100 subjects experiencing the onset of cold symptoms. We want one group of 50 to get vitamin C supplements, and one group of 50—the control group—not to receive them.

How do we decide who gets placed into which group? We could ask for volunteers. But doing so might create a systematic difference between the two groups. People who hear “vitamin C” and think, “yeah, that’s the group for me” might be people who are more inclined to eat fruits and vegetables, for example, and might therefore be healthier on average than people who are turned off by the idea of receiving vitamin C supplements. This difference between the groups might lead to different results in how their colds progress.

Instead of asking for volunteers, we might just assign the first 50 people who show up to the vitamin C group, and the last 50 to the control group. But this could lead to differences, as well. The people who show up earlier might be early risers, who might be healthier on average than those who straggle in late.

The best way to avoid systematic differences between test and control groups is to randomly assign subjects to each. We refer to studies conducted this way as randomized controlled studies. And besides randomization, other measures can be taken to improve reliability. The best kinds of controlled studies are “double-blind.” This means that neither the subjects nor the people conducting the study know which group is the control and which group is receiving the actual treatment. (This information is hidden from the researchers only while the study is ongoing; they are told later, of course, so they can interpret the results.) This measure is necessary because of the psychological tendency for people’s observations to be biased based on their expectations.

For example, if the control group in our vitamin C experiment knew they were not getting any treatment for their colds, they might be more inclined to report that they weren’t feeling any better. Conversely, if the members of the group receiving the vitamin supplements knew that they were getting treated, they might be more inclined to report that their symptoms weren’t as bad. This is why the usual practice is to keep subjects in the dark about which group they’re in, giving a placebo to the members of the control group. It’s important to keep the people conducting the study “blind” for the same reasons. If they knew which group was which, they might be more inclined to observe improvement in the test group and a lack of improvement in the control group. In addition, in their interactions with the subjects, they may unknowingly give away information about which group was which via subconscious signals.

Hence, the gold standard for medical research (and other fields) is the double-blind controlled study. It’s not always possible to create those conditions—sometimes the best doctors can do is to use the Method of Agreement and merely note commonalities amongst a group of patients suffering from the same condition, for example—but the most reliable results come from such tests. Discovering causes is hard in many contexts. Mill’s Methods are a useful starting point, and they accurately model the underlying inference patterns involved in such research, but in practice they must be supplemented with additional measures and analytical rigor in order to yield definitive results. They can give us clues about causes, but they aren’t definitive evidence. Remember, these are inductive, not deductive arguments.

Exercises

1. What is meant by the word “cause” in the following— indicate if “cause” means necessary condition, sufficient condition, or mere tendency?
   1. Throwing a brick through a window causes it to break.
   2. Slavery caused the American Civil War.
   3. Exposure to the cold causes frostbite.
   4. Running causes knee injuries.
   5. Closing your eyes causes you not to be able to see.

2. Consider the following scenario and answer the questions about it:

Alfonse, Bertram, Claire, Dominic, Ernesto, and Francine all go out to dinner at a local greasy spoon. There are six items on the menu: shrimp cocktail, mushroom/barley soup, burger, fries, steamed carrots, and ice cream. This is what they ate:

• • Alfonse: shrimp, soup, fries
  • Bertram: burger, fries, carrots, ice cream
  • Claire: soup, burger, fries, carrots
  • Dominic: shrimp, soup, fries, ice cream
  • Ernesto: burger, fries, carrots
  • Francine: ice cream

That night, Alfonse, Claire, and Dominic all came down with a wicked case of food poisoning. The others felt fine.

1. 1. Using only the Method of Agreement, how far can we narrow down the list of possible causes for the food poisoning?
   2. Using only the Method of Difference, how far can we narrow down the list of possible causes for the food poisoning?
   3. Using the Joint Method, we can identify the cause. What is it?

3. For each of the following, identify which of Mill’s Methods is being used to draw the causal conclusion.
   1. A farmer noticed a marked increase in crop yields for the season. He started using a new and improved fertilizer that year, and the weather was particularly ideal—just enough rain and sunshine. Nevertheless, the increase was greater than could be explained by these factors. So he looked into it and discovered that his fields had been colonized by hedgehogs, who prey on the kinds of insect pests that usually eat crops.
   2. I’ve been looking for ways to improve the flavor of my vegan chili. I read on a website that adding soy sauce can help: it has lots of umami flavor, and that can help compensate for the lack of meat. So the other day, I made two batches of my chili, one using my usual recipe, and the other made exactly the same way, except for the addition of soy sauce. I invited a bunch of friends over for a blind taste test, and sure enough, the chili with the soy sauce was the overwhelming favorite!
   3. The mere presence of guns in circulation can lead to higher murder rates. The data are clear on this. In countries with higher numbers of guns per capita, the murder rate is higher; in countries with lower numbers of guns per capita, the murder rate is correspondingly lower.
   4. There’s a simple way to end mass shootings: outlaw semiautomatic weapons. In 1996, Australia suffered the worst mass shooting episode in its history, when a man in Tasmania used two semiautomatic rifles to kill 35 people (and wound an additional 19). The Australian government responded by making such weapons illegal. There hasn’t been a mass shooting in Australia since.
   5. A pediatric oncologist was faced with a number of cases of childhood leukemia over a short period of time. Puzzled, he conducted thorough examinations of all the children, and also compared their living situations. He was surprised to discover that all of the children lived in houses that were located very close to high-voltage power lines. He concluded that exposure to electromagnetic fields causes cancer.
   6. Many people are touting the benefits of the so-called “Mediterranean” diet because it apparently lowers the risk of heart disease. Residents of countries like Italy and Greece, for example, consume large amounts of vegetables and olive oil and suffer from heart problems at a much lower rate than Americans.
   7. My daughter came down with what appeared to be a run-of-the-mill case of the flu: fever, chills, congestion, sore throat. But it was a little weird. She was also experiencing really intense headaches and an extreme sensitivity to light. Those symptoms struck me as atypical of mere influenza, so I took her to the doctor. It’s a good thing I did! It turns out she had a case of bacterial meningitis, which is so serious that it can cause brain damage if not treated early. Luckily, we caught it in time and she’s doing fine.