5 Symbolic Translations

Why Translate Statements?

We have seen that many arguments can appear compelling even when they lack logical force. The strategies employed to dupe us (or simply those that catch us off guard) are embedded in what we will call “natural languages.” These arguments are expressed in existing spoken, written, or signed languages. This text is written in English, so we have thus far looked at arguments in that natural language. And of course, we see that it can get us in an awful lot of trouble.

The difficulty we often find is that natural language use is highly complex. As J. L. Austin pointed out long ago, we do things with words. While we want to be sensitive to the nefarious things people do with language (see: Informal Fallacies), we also want to focus our efforts on one of the most important things we do with language: understand the meaning of claims.

You might think that this is obvious: “I mean, I speak English, so I understand it when I hear it.” How we wish that were so…

I often think studying logic might be easier if it were conveyed in an ancient Germanic tongue or some rare dialect of the Inuit people. If it were, most of us would probably pay very close attention to what was being said. We would try. Sadly, because most arguments are conveyed in a language we speak, we tend to think we do not need to try—the job of understanding has already been done! This is not so. Yet there is a clue here to how we can help ourselves avoid this error. If someone did convey an argument in the Inuit language, we would need a translation—something that helps us understand what was originally said.

Welcome to symbolic translations! We translate statements in one language (English) to another (our symbolic language) for the same reason we translate the Inuit arguments: to understand them. This only seems odd at first because of our false assumption that we already understand what people are saying when they are speaking a language we speak. Many of us know this to be false because we have seen people argue from a third-party perspective. We were not in it, we did not have a dog in that fight, and from that perspective we often note how people frequently miss the whole point of what the other person was saying. Two people, apparently speaking the same language, can fail to communicate effectively with one another…and the same thing is happening in our own heads.

Once we realize that there is a part of your brain that is trying to communicate with another part of your brain, we should recognize the danger of misunderstanding. What one part says, the other part only believes it understands. A good translation might help the other part grasp things more clearly. A good translator is needed, one well-trained at identifying what is needed in the moment and to the greatest benefit of the recipient. That will be you.

Starting with Statements

We begin the study of logic by building a precise logical language. This will allow us to do at least two things: first, to say some things more precisely than we otherwise would be able to do; second, to study reasoning. We will use a natural language—English—as our guide, but our logical language will be far simpler, far weaker, but more rigorous than English.

We must decide where to start. We could pick just about any part of English to try to emulate: names, adjectives, prepositions, general nouns, and so on. But it is traditional, and as we will see, quite handy, to begin with whole sentences. For this reason, the first language we will develop is called “the propositional logic.” It is also sometimes called “the sentential logic” or even “the sentential calculus.” These all mean the same thing: the logic of sentences.

In this propositional logic, the smallest independent parts of the language are sentences. Throughout this book, I will assume that sentences and propositions are the same thing in our logic, and I will use the terms “sentence” and “proposition” interchangeably. Our preferred term will be “statements” to mean the same thing. The term “statements” is more precise and, as we will shortly see, helps clarify distinctions between some natural language “sentences” and proper propositions of logic.

There are of course many kinds of sentences. To take examples from our natural language, these include:

What time is it?

Open the window.

Damn you!

I promise to pay you back.

It rained in Central Park on June 26, 2015.

We could multiply such examples. Sentences in English can be used to ask questions, give commands, curse or insult, form contracts, and express emotions. But the last example above is of special interest because it aims to describe the world. Such sentences, which are sometimes called “declarative sentences,” or better yet, “declarative statements,” will be our model sentences for our logical language. We know a declarative sentence when we encounter it because it can be either true or false. This is why we will benefit from the term “statement” to distinguish these important uses of language from other uses that have a different relationship to truth. Consider some of the above examples of English sentences:

What time is it?

Damn you!

If I ask you if either of these are true or false, you might look at me strangely. They are, of course, English sentences, but they bear a different relationship to truth. The first does not bear any truth or falsehood—rather, it inquires into the truth. The second also does not bear any truth, rather (at best, in its most classic sense), it seeks to change the truth of a future state. As we move forward, we will do well to keep in mind that logicians are concerned only with those sentences that can be true or can be false. So when we say “sentence” we mean “statement.”

Truth Value and Precision in Sentences

We want our logic of declarative sentences to be precise. But what does this mean? We can help clarify how we might pursue this by looking at sentences in a natural language that are perplexing, apparently because they are not precise. Here are two.

Tom is kind of tall.

When Karen had a baby, her mother gave her a pen.

We have already observed that an important feature of our declarative sentences is that they can be true or false. We call this the “truth value” of the sentence. These two sentences are perplexing because their truth values are unclear. The first sentence is vague; it is not clear under what conditions it would be true, and under what conditions it would be false. If Tom is six feet tall, is he kind of tall? There is no clear answer. The second sentence is ambiguous. If “pen” means writing implement, and Karen’s mother bought a playpen for the baby, then the sentence is false. But until we know what “pen” means in this sentence, we cannot tell if the sentence is true.

Since ancient times, philosophers have believed that we will deceive ourselves, and come to believe untruths, if we do not accept a principle sometimes called “bivalence,” or a related principle called “the principle of non-contradiction.” Bivalence is the view that there are only two truth values (true and false) and that they exclude each other. The principle of non-contradiction states that you have made a mistake if you both assert and deny a claim.

We can take these observations for our guide: we want our language to have no vagueness and no ambiguity. In our propositional logic, this means we want it to be the case that each sentence is either true or false. It will not be kind of true, or partially true, or true from one perspective and not true from another.

We can formulate our own revised version of the principle of bivalence, which states that:

Principle of Bivalence: Each sentence of our language must be either true or false: not both, not neither.

Some readers may be thinking: what if I reject bivalence, or the principle of non-contradiction? If you have doubts about bivalence, or the principle of non-contradiction, stick with logic. That is because we could develop a logic in which there were more than two truth values. Logics have been created and studied in which we allow for three truth values, or continuous truth values, or stranger possibilities. The issue for us is that we must start somewhere, and the principle of bivalence is an intuitive way and—it would seem—the simplest way to start with respect to truth values. Learn basic logic first, and then you can explore these alternatives.

The Correspondence Theory of Truth

Our starting point will embrace both principles of bivalence and non-contradiction. We will also embrace an intuitive concept of truth value^[1]: correspondence with the facts of the world. This is easiest to understand if we think of our terms as technical terms. The term “true” is not the same as the term “factual.” One (truth value) is a property of a statement. The other (fact) is a property of the world. Put differently:

The world be whatever it may be. What we say in an attempt to declare that things are so is an entirely different matter.

So, we should recognize that when we make a statement, we are not creating the world. We are attempting to capture it, to describe it, to understand it. Our words, our statements, are accountable to the world. They try to describe the world in a certain way, and they either get it right or they muck it up in some way. The world be what it be(those are the facts)—our attempts to describe it are the things that can succeed or fail (those are things that we call true or false).

This correspondence theory of truth is pretty intuitive and common. Most of us walk around on a daily basis adhering to this notion of truth value.

Ken: Honey, where are my keys? I left them on the kitchen counter last night.

Molly: No dear, they’re not there. They’re in your coat pocket.

This might be how Ken sees things, and this is his attempt to describe the world. Did he get it right? You only have to go look at the relevant part of the world to find out. Ken’s statement is “false” because the world is not as he describes it. Molly’s statement is “true” because the world is as she describes it. The world itself is neither true nor false—our statements have that property. The world just has facts; it is in a certain way, in a particular state, and we try to capture those facts with our language. So we can say again: only statements have the property of truth value.

We all have some grasp of what “true” means, and this grasp will be sufficient for our development of propositional logic.

Analyzing Statement Structure

Our language will be concerned with declarative statements: statements that are either true or false, never both, and never neither. Here are some example statements:

2+2=4.

Malcolm Little is tall.

If Lincoln wins the election, then Lincoln will be president.

The Earth is not the center of the universe.

These are all declarative sentences. These all appear to satisfy our principle of bivalence. But they differ in important ways. The first two sentences do not have sentences as parts. For example, try to break up the first sentence. “2+2” is a function. “4” is a name. “=4” is a meaningless fragment, as is “2+.” Only the whole expression, “2+2=4,” is a sentence with a truth value. The second sentence is similar in this regard. “Malcolm Little” is a name. The “is tall” is an adjective phrase (we will discover later that logicians call this a predicate”). “Malcolm Little is” or “is tall” are fragments; they have no truth value. Only “Malcolm Little is tall” is a complete sentence.

Atomic Statements

The first two example sentences above are of a kind we call “atomic statements.” The word “atom” comes from the ancient Greek word “atomos,” meaning “cannot be cut.” When the ancient Greeks reasoned about matter, for example, some of them believed that if you took some substance, say a rock, and cut it into pieces, then cut the pieces into pieces, and so on, eventually you would get to something that could not be cut. In logic, our atomic statements cannot be cut up into smaller parts without losing something of great significance: truth value. They are the smallest possible thing that retains the property of truth value.

In logic, the idea of an atomic sentence is of a sentence that can have no parts that are sentences. We should see, much like their physical namesake, that atomic statements clearly do have parts—but those parts are not in themselves statements (they are “subatomic” particles that cannot directly bear truth value). Noticing these parts can be a helpful way to identify an atomic statement, which always has the form:

One Subject + One Predicate

Consider the following:

Kevin likes weightlifting.

Carl enjoys taking long walks along the River Thames.

The newest Shelby Mustang has over 600 horsepower.

My cousin Mary won a baking contest last year.

Each of these has one subject and one thing said of that subject. Note, however, that we are not saying “one word” is the subject of the statement. Subjects are often expressed in a single “term” that requires several words to detail. “My cousin Mary” is a single term, as is “the newest Shelby Mustang.” The speaker is only referring to one thing, even though they use several words to do it.

If we have a statement with more than one subject or more than one predicate, then we have something larger than an atomic statement. We’ll get to those in a bit. For now, we can see that statements like the following have more than one subject or more than one predicate:

Tom is a cat, and he eats mice.

Missy and Andrew got As on the exam.

My house is small but cozy.

The first and third have only one subject (one “thing” about which the statement attempts to describe). However, they also have two predicates (two different descriptions of that same thing). In the second example, there is only one description (one predicate) given, but it is given to two distinct subjects.

To express our understanding of these larger statements in our symbolic language will require a bit of work. However, to express our understanding of an atomic statement like “Tom is a cat” is easy. After all, the smaller bits in this sort of statement do not have a truth value, so for now they can be suppressed into one “atom” of a meaningful statement.

It is traditional in logic to use upper case letters from P on (P, Q, R, S….) to stand for atomic sentences. Thus, instead of writing

“Malcolm Little is tall.”

We could write

P

If we want to know how to translate P to English, we can provide a translation key. Similarly, instead of writing

“Malcolm Little is a great orator.”

We could write

Q

And so on. Of course, written in this way, all we can see about such a sentence is that it is a sentence, and that perhaps P and Q are different sentences. But for now, these will be sufficient.

Note that not all sentences are atomic. Recall the example given previously: If Lincoln wins the election, then Lincoln will be president.

This contains parts that are sentences. It contains the atomic sentence “Lincoln wins the election” and the atomic sentence “Lincoln will be president.” We could represent this whole sentence with a single letter. That is, we could let

“If Lincoln wins the election, Lincoln will be president.”

be represented in our logical language by

S

However, this would have the disadvantage that it would hide some of the sentences that are inside this sentence, and it would hide their relationship. We would have a translation that suppresses important meaning that is critical to a logical evaluation of the original statement. Our symbolic language would tell us more if we could capture the relationship between the parts of this sentence, instead of hiding it. So this would be a very poor translation of this statement.

Syntax and Semantics

An important and useful principle for understanding a language is the difference between syntax and semantics. “Syntax” refers to the “shape” of an expression in our language. It does not concern itself with what the elements of the language mean, just specifies how they can be written out.

We can make a similar distinction (though not exactly the same) in a natural language. This expression in English has an uncertain meaning, but it has the right “shape” to be a sentence:

Colorless green ideas sleep furiously.

In other words, in English, this sentence is syntactically correct, although it may express some kind of meaning error.

An expression made with the parts of our language must have correct syntax in order to be a sentence. Sometimes, we also call an expression with the right syntactic form a “well-formed formula” or WFF for short.

We contrast syntax with semantics. “Semantics” refers to the meaning of an expression of our language. Semantics depends upon the relationship of that element of the language to something else. For example, the truth value of the sentence “The Earth has one moon” depends not upon the English language, but upon something exterior to the language (i.e., the facts of the world that be this way). Since the self-standing elements of our propositional logic are sentences, and the most important property of these is their truth value, the only semantic feature of sentences that will concern us in our propositional logic is their truth value.

We should note that there are other semantic features of sentences that we will ignore in our efforts to translate into a symbolic language. This is an inevitable consequence of going from one language to another. Anyone who has ever translated from one language to another has come across times when they just shrug and say, “Sorry, there really isn’t a way to convey the same meaning of what they said in your language; there just isn’t a word for it in your language.” In these instances, we say some of the meaning was “lost in translation.” In logic, we sometimes refer to this as the sense of an expression. As we will see, this “sense” is frequently lost, yet the truth value remains.

We have so far introduced atomic sentences. The syntax for an atomic sentence is trivial. If P is an atomic sentence, then it is syntactically correct to write down

P

By saying that this is syntactically correct, we are not saying that P is true. Rather, we are saying that P is a sentence. Fortunately, in a proper translation we will always provide a key to understand what each atomic statement means in English. These keys have different names in different logic texts. We see them referred to as:

Translation Scheme

Scheme of Abbreviation

Universe of Discourse

These terms all mean the same thing: a key to tell us what each atomic (each capital letter) means in the present translation. If you are provided a translation scheme, you should use it. However, if you are given no translation scheme, you should most definitely write it out completely so that it accompanies your translation of the larger statements.

Compound Statements

Statements larger than atomics are usually composed of multiple atomic statements. These go by different names. Generally, we refer to these as compound statements, but they are also called “complex” statements and “molecular” statements (because they are composed of more than one atomic, a play on the physical analogy). However, strictly speaking, a compound is any statement that has greater logical form than an atomic. So all the following are compounds:

Ford and Chevy make muscle cars.

That forest has oak trees and is home to many woodland critters.

I did not go to the store.

If we go to the movies, we’ll get some popcorn or nachos.

The savvy student will note that some of these statements have more than one subject. Some have more than one predicate. The third example may seem like it does not belong on the list, because there is one subject, and we say one thing about it. However, a closer look reveals that what we say about that one subject is more complex in its logical form than what we see in atomics. Let’s break it down:

Subject: “I…”

Predicate: “…did not go to the store.”

Question: Well, where did I go then?

Notice that you cannot answer this question. The statement does not declare where I actually went. This statement tells us nothing about my real activity—it makes no attempt to assert something definitive. This is very different from an atomic statement, which we defined as a simple declarative statement. The atomic statement “I went to the store” does quite definitively describe where I went (once we clarify or denote which store). If I ask my question again: Where did I go? This statement provides us with a substantive answer.

However, our statement “I did not go to the store” does something very different—it denies a declaration of my trip’s destination. In doing so the speaker has taken a definite statement and then said “no” to the truth of that statement. In terms of the logical structure of their statement, that’s more complex than an atomic. Their statement is a compound—in this case, not in the sense of combining more than one atomic, but of still doing more with one atomic than simply asserting it.

Put simply: atomic statements always make a single affirmative assertion about a single subject. If you are doing more than that, you are making a compound statement.

When we make compound statements, we are performing logical operations on smaller statements. This is what we do. We are not content to think, reason, believe, and communicate things about the world in the simplistic manner of atomic statements. We see important relationships in the world and need a way to express our understanding of these. Enter: logical operators.

Logical Operators

Strictly speaking, we should introduce these as truth-functional logical operators. The reason is that when we do things with smaller statements, we sometimes do them in a way that has a direct impact on the truth of the larger statements we make. Put differently, when a larger statement has been made by using these logical operators, the truth of these larger statements can be determined by the truth value of the smaller statements. Truth-functional operators take in the truth value of the component statements and spit out a new truth value depending on the nature of the logical operation being performed. Consider these intuitive examples and see if you can sense when the following examples are true and when they are false:

I went to the store, and I went to the bank.

I went to the store, or I went to the bank.

Our speaker is talking about the exact same thing (themselves), and even describing that thing in the same ways. Yet we see that these two statements are very different in their truth values. The second statement may be true at the exact same time that the first statement is false. This is because the two compound statements were made in a different way that bears directly on the truth value of the whole statement. The compounds here were both made with truth-functional logical operators.

Logical operators are also sometimes called “statement connectives” (or “truth-functional connectives”) because of the role they play in constructing larger compound statements. They act like a kind of glue to bond together atomic statements (or, to again play off of our physical analogy, these are the bonds of our molecules). However, the first of these (which we just saw above) does not really bond together statements, it simply performs a logical operation on a statement—it denies it. We will review this as well as four other logical operators to help flesh out our symbolic language.

Table of Logical Operators

Operator Name	Common Name	Symbol	Symbol Name
Negation	“not”	~	(tilde)
Conjunction	“and”	∙	(dot)
Disjunction	“or”	v	(vee)
Material Conditional	“if, then”	→	(arrow)
Material Biconditional	“if and only if”	↔	(double arrow)

In our text, we will use these symbols to represent the important logical operations speakers make when constructing their compound statements. You will find some variation in the symbols used in other logic textbooks. You will likely also find the same (or similar) operators in a math or a computer programming textbook, and these often use different symbols. If you use those symbols to translate, your math teacher will be oh so very proud. Your logic teacher, on the other hand, will wonder why you are translating into a different language—much like your German teacher does not care if you are familiar with negation as it is expressed in the Russian language (“nyet”)—they want to see that you can translate the English “no” into what is proper for that class (“nein”).

Negation

Our previous example helps us recognize the basic function of the negation:

I did not go to the store.

Negations are denials of other statements. Our translation scheme for these is rather easy. We simply insert a “~” in front of whatever statement we want to deny. In this case, someone wants to claim:

I went to the store.

Translation: S

I deny that this is true. I say:

I did not go to the store.

Translation:~ S

We can always deny a statement. We’re not always right when we do, but in principle the negation is a simple function. The only real question is whether we are denying a simple atomic statement (as above) or whether we are denying a compound statement. After all, my friend may predict:

If you go to the store, you will get some milk.

Translation (we’ll see this in a bit):

S → M

I am always at liberty to reject this claim. In doing so, I should be careful that I do not deny some other claim—I want to deny my friend’s claim. So I will not say:

I won’t go to the store.{ translated as ~ S }

Nor will I say:

I won’t get some milk.{ translated as ~ M }

Those would not deny what my friend said, for they never said I would go to the store, nor did they say I would get some milk. They said IF I go to the store, THEN I’ll get some milk. They expressed a relationship between these two claims. So, I need to deny that relationship. I will not deny the individual statements, nor express the same relationship my friend expressed but with each part denied { ~ S → ~ M }. That will not do either. I will deny the relationship itself.

To do so, I will likely say something like:

It is not true that if I go to the store, then I will get some milk.

Translation: ~ ( S → M )

Conjunction

Conjunctions are unions of two statements. The speaker wishes to assert two things within a single sentence. The two “things” may be about two separate subjects, or they may be two different descriptions about a single subject. For example:

Brandon and Lily go to college.

Brandon goes to college and studies economics.

Both of these are conjunctions. We may find it easier to paraphrase compounds such as this to make the two statements clear. For example:

Brandon goes to college, and Lily goes to college.

Brandon goes to college, and he studies economics.

Now each part of the conjunction is fully and explicitly expressed. Later this will help us to translate these statements. This is especially true when we come across larger conjunctions whose parts are themselves compound statements. In these examples, our translation scheme would be (respectively):

B ∙ L

B ∙ E

For now, let’s just note that we will often need to talk about the two components of a conjunction. We call each part a “conjunct” and distinguish them by left side/right side. Only conjunctions have conjuncts.

Disjunction

We use disjunctions to express alternatives between two statements. The most common way is to use “or” to divide them up. As with all other compounds, these two options can be regarding a single subject, or they can be options between two different subjects (or a combination of these). Consider:

Mark will plant the garden or he will sleep in.

Mark or Tom will plant the garden.

Mark will plant the garden alone, or Tom will sleep in.

The translation schemes for these would be as follows:

M v S

M v T

A v B

The savvy student will note that we had to take care not to confuse our atomics. The claim that “Mark will plant the garden alone” is a different claim than simply “Mark will plant the garden.” Thus, they require different translations into different capital letters. Likewise, the claim “Mark will sleep in” is clearly a different statement than “Tom will sleep in.” So they too required different translations.

As we will see below, there are several other ways to express disjunctions. What matters now is that we need to understand that the logical operator of disjunction expresses a very liberal view of these options. The best way to express it in English is likely:

At least Mark or Tom will plant the garden.

The reason this helps is that it reveals to us that we are making a very, very weak statement. The logical disjunction is a noncommittal statement. The speaker is not going very far out on a ledge to assert much of anything. They simply want to establish the options—but hey, don’t hold me to that—I mean, those options might even include the one where both Mark and Tom do the gardening. This is why we call the logical disjunction an “Inclusive-Or” statement. A logical disjunction includes the possibility that both sides of the disjunction come out true…it also includes the possibility that only the left side is true…it also includes the possibility that only the right side is true. See: very weak, very noncommittal.

We call each side of the disjunction a “disjunct,” and as with the conjunction, they are distinguished by left side/right side. Only disjunctions have disjuncts.

Material Conditional

Consider the following example:

“If Lincoln wins the election, then Lincoln will be president.”

We could treat this like an atomic sentence, but then we would lose a great deal of important information. For example, the sentence tells us something about the relationship between the atomic statements “Lincoln wins the election” and “Lincoln will be president.” To make these relationships explicit, we will have to understand what “if…then…” means. Thus, it would be useful if our logical language were able to express these kinds of sentences in a way that makes these elements explicit. Let us start.

The sentence “If Lincoln wins the election, then Lincoln will be president” contains two atomic sentences: “Lincoln wins the election” and “Lincoln will be president.” We could thus represent this sentence by letting

“Lincoln wins the election”

be represented in our logical language by

P

And by letting

“Lincoln will be president”

be represented by

Q

Then, the whole expression could be represented by writing

If P then Q

It will be useful, however, to replace the English phrase “if…then…” with a single symbol in our language. Our symbol is “→.” Thus, we would write

P→Q

This kind of sentence is called a “material conditional.” It is also often simply called a “conditional.” The first constituent sentence (the one before the arrow, which in this example is “P”) is called the “antecedent.” The second sentence (the one after the arrow, which in this example is “Q”) is called the “consequent.”

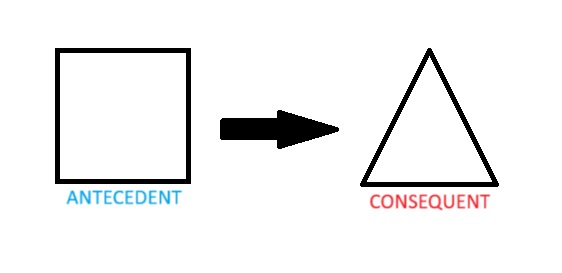
One last thing needs to be observed, however. We might want to combine this complex sentence with other sentences. In that case, we need a way to identify that this is a single sentence when it is combined with other sentences. There are several ways to do this, but the most familiar (although not the most elegant) is to use parentheses. Thus, we will write our expression

(P→Q)

This is useful when we want to say something like:

“I think Douglas will win easily, but admit that if Lincoln wins the election then Lincoln will be president”

If we let “I think Douglas will win easily” be translated as

D

Then the whole expression translates as

D ∙ (P→Q)

Note how the parentheses help our translation stay true to the original English expression. As we will see shortly, without these in place, our symbolic translation could be interpreted in a very different manner than what our original English speaker intended.

Material Biconditional

Strictly speaking, we don’t really need the logical operator that does the work of the material biconditional. We could get by translating what people say using a combination of and, or, and if-then quite easily. The trouble is, this may be too easy in many cases. We may be inclined to mistranslate what people intend if we don’t have something to reference that would make their original intent clear. Enter: the Material Biconditional.

Biconditional statements are what most people actually hear when they hear a conditional statement. They hear a very tight relationship between what is said on one side and what is said on the other side. For example:

If you do the dishes, then I’ll take you to get some ice cream.

A proper translation would be:

D → I

People who hear this often hear that each side is somehow dependent upon the other. This is false. So, not surprisingly, this usually leads to error and confusion. Therefore, we find it is quite helpful to have a way to explicitly express (and distinguish) the relationship of a conditional statement (→) from the tighter relationship expressed in the biconditional. The name is different, the symbol is different (↔), and the conditions of truth are different. All of this is helpful in communicating clearly what we intend.

I’ll take you to get some ice cream if and only if you do the dishes.

That’s what most people heard when they read the first statement. And if that is what was intended, the original speaker misspoke and would do well to take a logic class. This would help everyone else focus in on what relationship was intended in the speaker’s claim. We could easily translate this as:

I ↔ D

On the other hand, if the original speaker really did mean to express a single material conditional, then the rest of us would do well to listen more carefully to what they were saying and not put words (or meaning) in their mouth. Our translation would not make use of the double arrow.

There is no special name for each side of the material biconditional.

GRAMMAR—WELL-FORMED FORMULAS

We have already introduced the concept of syntax—the form of a statement. All languages have rules for syntax, and we typically think of this as their grammar rules. These are standards to ensure that the form of the expressions we make are consistent for all users and that the statements we make clearly communicate our desired meaning.

In our symbolic language, we need rules to make sure that the statements we express unambiguously reflect the meaning of those we are translating. Fortunately, there are only a small number of these rules. We refer to them as the conditions of “well-formed formulas,” or “WFFs” (pronounced “wiffs”) for short.

Statement Variables

To learn these rules we need to introduce another concept: the statement variable. A statement variable is (like all other variables) just a placeholder for a statement. Unlike atomic statements, statement variables do not actually say anything—they just act like a marker for a statement of some kind that does say something. What is most important is that we understand that these placeholders do not presuppose what kind of statement they represent: they could stand for an atomic or any kind of compound statement. They are simply blank spots, and they help us talk about the general form of a statement. We will use the following to represent statement variables:

□ (box)

△ (triangle)

On rare occasion we will have cause to use two other statement variables:

◯ (circle)

✩ (star)

In all cases, it should be clear that these are just symbols that represent the presence of some kind of symbolic statement. None of them have any priority nor preference; they do not exclude one another, nor insist upon difference (i.e., the statement that we eventually find inside a box can be the exact same statement we eventually find inside a triangle, etc.). They are simply empty spots in which a symbolic statement will go.

Many logic textbooks take their cues from math textbooks and use letters for statement variables. So you will see this:

“p,” “q”

Or even worse:

P , Q

You might also see Greek letters used:

ϕ , ψ

These are exceedingly unfortunate (the Greek is tolerable; the rest are counterproductive). We have just learned that “capital letters” are used in our symbolic language to represent atomic statements. So why muddy the waters with more letters?

These ways of symbolizing statement variables dupe many students into thinking you are only allowed to insert atomic statements in these spots—this is NOT true. Unfortunately, the rest of the logic world has not caught on to this troublesome conflation. So let’s set the record straight:

A statement variable can contain any statement.

We will use boxes and triangles, because after all, anything can fit inside a box (you just need a big enough box).

There are only six grammar rules in our symbolic language. They are as follows:

Note that we use the ( ) to begin and end our grammatically correct expressions in our symbolic language. This is much like the English rule of starting every sentence with a capital letter and ending with an appropriate punctuation (generally a period when a statement is made). We are well-served when we know clearly when an expression begins and when it ends.

We will make use of two conventions that help us clean up the visual appearance of larger compounds. These two are as follows:

1. Drop the outermost parentheses (you must always retain the inner parentheses)
2. Alternate ( ) with [ ] to group smaller compounds in a larger compound

For example, strictly speaking, the following is a WFF:

( A v B )

This statement conforms to the 4^th condition for WFFs. We see a statement that perfectly conforms to the pattern:

( □ v △ )

We read this as: open parenthesis, A, v, B, closed parenthesis. When we look inside the □ and the △ positions we see atomic statements (which are WFFs by the 1^st condition for WFFs). This is all well and good, but let’s face it, nobody is going to be confused about the meaning of our statement if we just say:

A v B

That’s perfectly clear, even though we dropped the outermost parentheses (and in this case, the only parentheses). However, if our statement were more robust, we would quickly find our statements are not clear if we start dropping all the parentheses. For example, I may want to say:

( ~ R → ( A v B ) )

We can clean this up by dropping the outermost parentheses:

~ R → ( A v B )

Again, there is no risk of confusion in doing this. We can readily tell what the box is and what the triangle is in this case.

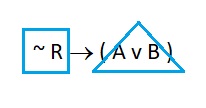
However, consider this formula:

~ R → A v B

What do I mean by this formula? I could mean:

( ~ R → A ) v B

I could also mean:

~ ( R → ( A v B ) )

Or I could mean:

~ ( R → A ) v B

All of these variations mean something completely different. Once we drop all the parentheses, our symbolic statement becomes highly ambiguous. This is not good. We do not run this risk if we are just dropping parentheses that would belong on the outside of our statement’s main components. However, anything INSIDE a box or a triangle needs to retain the parenthesis if it is a compound statement that requires them in the Six Conditions for WFFs.

Just to clarify:

Atomic statements do not require any parentheses.

Negations do not require any parentheses UNLESS what is inside their box is a compound

This last point deserves an illustration. So consider:

~ M v L

This is a WFF by our first convention. It satisfies the 4^th condition for WFFs.

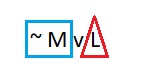
However, the following statement does not satisfy the 4^th condition; it satisfies the 2^nd condition:

~ ( M v L )

Here we have a negation: a statement that satisfies the 2^nd condition for WFFs. What is inside the box is a disjunction—it is inside the box of ~ □, so it must retain the full account of the 4^th condition for WFFs. This means that it must retain the parentheses.

On the other hand, look again at our first example:

~ M v L

Notice how we have a statement that conforms to ( □ v △ ) without the outermost parenthesis.

Condition 4 tells us that this is fine so long as what is inside the □ and △ are also WFFs. Inside the □ is the statement:

~ M

This conforms to the 2^nd condition for WFFs:]

~ □ is a WFF, if and only if □ is a WFF

Now when we look inside this little □, we find an atomic statement.

The 1^st condition for WFFs tells us that atomics are WFFs all by themselves—there should NO parentheses around it. So, no parentheses around a negation and no parentheses around an atomic.

Last, a quick word on our second convention that allows us to alternate ( ) with [ ] (we call the latter “brackets”). This just helps us see the groups of compound statements when statements get very large. Consider the following:

~ [ ( N → A) v ( [ M v K ] → U ) ]

The brackets simply help us recognize the fact that this is a giant negation (and more precisely, this is a negation of an Or statement:

~ [ ( N → A) v ( [ M v K ] → U ) ]

For most folks, things can get blurry when we only use parentheses:

~ ( ( N → A) v ( ( M v K ) → U ) )

The brackets help a bit.

There is no hierarchy between ( ) and [ ] as there is with English punctuation (commas are subordinate to semicolons). So the translator is at liberty to use them as they see fit, so long as we are not mix and matching the opening and closing punctuation (i.e., if you open with a bracket, you must close with a bracket, etc.).

The Main Connective

We should note that the second half of each condition for WFFs stipulates that the component parts of a compound statement must themselves be grammatically correct. This is extremely important and helpful. In larger compounds we may find it difficult to tell what kind of statement is being asserted. Knowing that the grammar rules require each part of a large compound to be grammatically correct means we have a way to test a statement to see if it is this or that kind of compound. Let’s look at the last example:

~ [ ( N → A) v ( [ M v K ] → U ) ]

This is a challenging statement to identify at first. We may not know what kind of statement it is, but the WFF rules remind us that however it is carved up, each component must be a WFF. So we can test it.

Say our gut tells us that this is an “or” statement (a negation). If so, then there are a □ and a △ that must themselves be WFFs.

To the left of the “v” we see this:

~ [ ( N → A)

To the right of the “v” we see this:

( [ M v K ] → U ) ]

Are either of these WFFs? No. So our gut misled us, and we know that this is not an “or” statement. In fact, if we thought we could use the other “v” to identify this as a grammatically correct statement, the situation becomes worse. To the right of that “v” we see:

K ] → U ) ]

This is clearly not a WFF.

Keep going: try every operator up there and you will find only one that produces a □ or a △ that is a WFF. This turns out to be the “~” operator. Like all ~ □ statements, to the right of the “~” must be a WFF. In this case we see:

[ ( N → A) v ( [ M v K ] → U ) ]

Note that we are inside a □ now, so the outer brackets must be retained. This makes the statement here conform to the 4^th condition for WFFs. We could continue to break this statement down into each of its component parts until we arrived at the smallest units, the atomics. Like this:

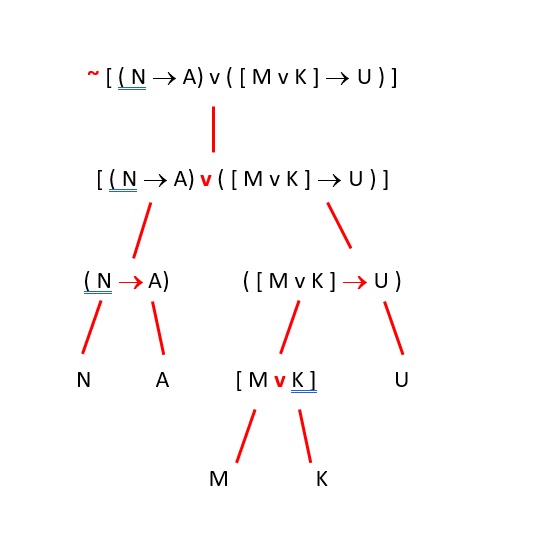
You can do this exercise with any size compound statement. Indeed, making a tree diagram like this is helpful practice to train your eyes to start identifying the main connective of every statement. Doing so will vastly improve your ability to perform on just about everything we do in logic from this point forward.

The main connective (the MC) is one of the single most important concepts you will need to master to pass a logic class. We can understand the MC as having three defining features:

1. The MC is the last logical operator used to construct a statement
   (It is the last in working your way UP from atomics to the final statement at the top of your tree diagrams.)
2. The MC is the bearer of truth for a statement
   (We will see this later in our work on truth tables.)
3. The MC is the identity of the statement
   (We see this now in how statements conform to one of the conditions for WFFs, but we will make heavy use of this feature when we do logical derivations or logical proofs.)

Practice making tree diagrams until you get very good at just looking at a statement and identifying what kind of operator is the Main Connective.

Linguistic Variants

There are many ways to express logical operators in a natural language. We call these “alternate phrasings” or “linguistic variants of the logical operators.”

Since we are working in English, we will look at some of the most common ways the English language captures these logical operations. One general word of warning: like most natural languages, English is very robust and allows speakers to use the same terms in different ways. Put differently, not every instance of a linguistic variant is being used as a logical operator. For example:

Tom and Jerry were great characters.

Tom and Jerry was my favorite cartoon.

In the first statement the “and” is being used as a logical operator. We would do well to paraphrase that statement as:

Tom was a great character, and Jerry was a great character.

In the second statement (“Tom and Jerry was my favorite cartoon”), this is not how the speaker is using the “and” in their statement, for it is simply a part of the name of that one show. In other words, we would not want to paraphrase the second sentence as:

Tom was my favorite cartoon, and Jerry was my favorite cartoon.

Heck, there wasn’t even a cartoon named “Jerry,” so this would be a terrible paraphrase and result in an incorrect translation. We’ll try to note some of these non-logical uses of the linguistic variants along the way.

Negation

Denials are almost always intended, so we rarely have to worry about a speaker using an English variant of the negation in any way other than to actually mean “No, that claim is not true.” Common variants are:

“…not □”

“…n’t □”

It is false that □

□ is not true.

The claim □ is wrong.

□ is not so.

□ can’t be the case.

I don’t believe □.

Despite what we just said about not having to worry about variations in meaning, we can see a few cases here where a speaker may be expressing a subtle claim. For example, “I don’t believe □” usually means ~ □. However, the speaker may be very cagey and only intend to say something about themselves. They may not intend to deny the truth of what was said about the world, but rather deny the content of their own mind. Cagey.

Additionally, the phrase “□ can’t be the case” is usually meant in a colloquial voice to mean ~ □. We may blurt this out when we are surprised or were convinced we would discover something different. However, if we strictly adhere to the phrase, it means something stronger than “□ is not true”—it means “□ cannot be true” (it is impossible). This is a much stronger denial than what we typically mean when we say something like “The lights are not on”—I only mean they are not on at the moment, I don’t mean it is impossible for them to be on. For purposes of translation, we will get by with the casual meaning of these variations and go with a simple schematic of ~ □.

CAUTION

One word of caution regarding negations is in order. Many people conflate conceptual opposites with logical negations. Some ideas have counterpoints that we associate with them. For example, I say “dog” to you and ask, what’s the opposite? You might say the opposite of “dog” is “cat.” We hold dogs/cats as some kind of conceptual pair. Of course, there is nothing denied in “cat” that is expressed in “dog” (and cat/dog is only a conceptual pair in some countries). Still, people may act as though they are opposites. For example:

Mary: I had to rush my baby to the vet yesterday!

Peter: Oh no! What’s wrong with your dog?

Mary: Huh, I don’t have a dog.

Peter: Oh sorry, what’s wrong with your cat?

Mary: I don’t have a cat either—I have a snake.

We do this more frequently with tightly packed concepts. For example:

Howard: Darn, the team I bet on didn’t win yesterday.

Yuri: Sorry to hear they lost.

Howard: What? They didn’t lose, the game was a tie.

Winning and losing are conceptual opposites. They are not logical denials of one another. Howard spoke the truth when he said his team did not win. Yuri made the mistake of thinking he could “translate” that statement as:

L: Howard’s team lost

When he should have simply translated it as:

~ W (where W: Howard’s team won.)

Many people make such errors regarding logical negations. In translating, it is better to simply put a tilde in front of whatever the claim was rather than try to “think through” what we believe the speaker’s meaning was in offering the negation.

Last word of caution: beware the “n’t” hidden in many statements. If I say, “I didn’t go to the store,” we may find ourselves hiding the logical operation in this statement by translating it as an atomic (e.g., S). This would hide useful information regarding what was actually said. This tiny “n’t” is a logically significant move made by the speaker. We should strive to capture it faithfully in our translation.

Conjunction

The logical conjunction is well-captured with the English “and” in most cases. However, there is a range of other English terms that can be used to capture the basic form of □ ∙ △. The following are the most common English variants:

□, and △

□, yet △

□, as well as △

□, in addition to △

□, but △

□, however △

□, nevertheless △

□, even though △

Two things need to be addressed: rhetoric and a discomfort.

First, many English expressions use these terms for rhetorical effect. For example, I may start a statement with one of these: “However, we should also consider waiting for more information.” Strictly speaking, the “However” here is not used as a logical conjunction. This is just a smooth way to continue to the next statement. Oddly, for years English teachers instructed students to never begin their sentences with “But” while simultaneously encouraging many of the other openers as rhetorically viable options (e.g., “Yet, we might find it equally wise to contact the source for their input.”). To logicians, these are all the same—none of the openers are treated as logical operators.

Second, when we review our list of variants, we immediately see that some of these English terms contain a sense of contrast or denial that is not contained in the logical conjunction. So, if you have some reservations about translating “yet” or “but” as a conjunction, you’re not alone. Terms such as “nevertheless” and others often give the audience the sense of opposition between the two component statements. This does not come across in the logical conjunction; this sense of the original English is lost in translation. When we look at a statement such as:

I went to the store to buy milk, but orange juice was on sale.

Our translation would be:

S ∙ O

In our original English we never said “no” to anything. We affirmed that we actually went to the store. We also affirmed that orange juice was on sale. Both statements are affirmed. The sense of surprise or possible insinuation (not actually stated) that we did not get milk is lost in translation.

CAUTION

Be careful with this important variant:

Both □, and △

The addition of “both” should be treated as more than fluff. This is a useful way for our speaker to alert the audience that a conjunction is being formed. This is important when the speaker is trying to group two statements within the context of another logical operation. Consider the following:

Both Mike and Tom did not win.

Mike and Tom did not both win.

These two statements mean different things. They are true under different circumstances. And our author is trying to help us recognize their intent. We need to attend carefully to listen well. So which translation do you think belongs with which statement?

~ □ ∙ ~ △                                 ~ ( □ ∙ △)

Take a moment to listen carefully to how the author uses “both” in their two statements. The term “both” is like a flag; it alerts the audience that a dot is forthcoming. The question is, what is the nature of each conjunct?

In the first statement, we are alerted right away that two things are forthcoming: “Both □, and △.”

Inside the □ (as well as in the △), we find the claims about each not winning. We could paraphrase:

Both Mike did not win, and Tom did not win.

Thus, our translation schematic would follow the form:

~ □ ∙ ~ △

Yielding the actual translation:

~ M ∙ ~ T

In the second claim (Mike and Tom did not both win), the “both” again flags a grouping: “…both win.” However, in the English, this group is preceded by a denial of that grouping. A rough paraphrase would be:

It is false that both win.

Thus, our translation schematic would follow the form:

~ ( □ ∙ △)

Providing a full paraphrase makes the original English clear:

It is false that both Mike won and Tom won.

Our translation is now easy:

~ ( M ∙ T )

TIP: On Flags and Negations

Another way to look at this is to follow a simple rule that usually helps:

Negations negate what they immediately encounter

When we look at the English statements, we find an English “not” that runs right into something:

Both Mike and Tom did not win.

Mike and Tom did not both win.

In the first sentence, the English “not” immediately encounters the claim about winning. Which claim? Both claims. The one about Mike and the one about Tom. Thus:

~ M ∙ ~ T

In the second sentence, the English “not” immediately encounters the English flag “both,” so we translate this as a tilde that immediately encounters an open parenthesis that contains this type of grouping.

~ ( M ∙ T )

As we will see, other logical operators can be flagged by English words, and this same rule applies. Pay close attention to what the “not” or the ~ immediately encounter.

Disjunction

We have seen that the logical disjunction is, in a way, the opposite of a conjunction. Whereas the conjunction allows a speaker to affirm two things, the disjunction allows them to merely suggest that at least one of two options is true. There are several ways to express this relationship in English. For example:

□, or △

At least □, or △

□, unless △

Either □, or △

□, and/or △

The savvy student probably already notices that some of the variants include “flags” for the logical disjunction. After all, if I open my statement “Either…yaddah, yaddah, yaddah….” you (the audience) know that sooner or later I have to say “OR” and then continue my yaddahs. The “either” works well this way. The “at least” can also be used this way, but you will find some speakers use it excessively as a rhetorical device. For example,

At least clean your room once in a while.

This “at least” is not a flag for a disjunction. However, you will never see “either” used rhetorically.

Inclusive vs Exclusive Or

We already noted that the logical disjunction is an Inclusive Or. In English, the best way to properly capture this logical relationship is found in:

At least □, or △

Or stronger still: At the very least □, or △

□, and/or △

While I find some speakers prone to rhetorically use “and/or” for effect, this is entirely the fault of those speakers. The English “and/or” very clearly and explicitly expresses an Inclusive Or.

If we can ignore rhetorical flourish for a bit, we should consider that many speakers (and audiences) expect their English “or” to be received differently than what is meant by the logical disjunction. After all, if I say, “We’ll go to the movies or to the carnival tonight,” you probably think we’ll do only one or the other. Indeed, a better paraphrase for our sample statement here would be:

We’ll go to the movies or to the carnival, but not both.

This expresses the removal of one of the included options of the Inclusive Or. We call these “Exclusive Or” statements. They can be captured in our symbolic language by carefully translating our paraphrase.

We’ll go to the movies or to the carnival, but not both.

We should see that we have two things affirmed: here are the options, AND here is the denial of one of the included options we would find in a standard disjunction. So, this translates as:

( M v C ) ∙ ~ ( M ∙ C )

The main connective of this statement is the blue dot. What this reveals is that when a speaker intends to communicate an Exclusive Or, they are actually expressing a conjunction.

The Special Case of UNLESS

Some people are very frustrated with treating the term “unless” as a disjunction. Some just don’t like the term “unless” at all. Still, it causes enough trouble that we should address it here. There’s no shortage of people who hear a conditional statement when they hear “unless.” This is fine, so long as we know how to properly translate that conditional statement. Most folks get this wrong, because it takes quite a bit of thought and effort. Put differently, it can be tricky to correctly translate “unless” as a conditional statement.

Conversely, translating “unless” as a disjunction is very easy! All you have to do is put a “v” on top of the word “unless” and translate the left / translate the right / and done! Very easy, very little extra thought put into it. Here’s an example:

Either we get those reinforcements, or the fort will fall tonight!

Let’s think this through. We might translate this as a straight conditional statement:

R → F

However, if we read that back we get:

If we get those reinforcements, then the fort will fall tonight.

That’s clearly wrong. The speaker did not mean that; they meant something different. Something like this:

If we do not get those reinforcements, then the fort will fall tonight.

Now we can correctly translate their original statement into the proper conditional:

~ R → F

Here’s another way to do it. Remember the original statement:

Either we get those reinforcements, or the fort will fall tonight!

We can do as I suggest, and just slap a “v” over the “or” term:

Either we get those reinforcements, v the fort will fall tonight!

Translation:

R v F

Done.

The Special Case of NEITHER, NOR

Often, we hear people use the phrase “neither nor” to indicate a special relationship between the two smaller statements. We can properly translate this in two distinct ways. So, let’s try a test:

Neither Porsche nor Tesla make cars with a true American spirit.

What did you hear? See, most people probably heard our speaker make two denials. They hear:

Porsche does not make cars with a true American Spirit, and Tesla does not as well.

That’s something like what most people heard. So we can successfully translate this as a conjunction of the two denials:

~ P ∙ ~ T

Our speaker wants to deny both claims. That’s a good translation. However, some people (in my experience, they are the minority) hear something different. They hear an “either, or” statement…that was denied.

Neither Porsche nor Tesla make cars with a true American spirit.

These folks are also correct! So, we can successfully translate the same statement as the Negation of an Or statement:

~ ( P v T )

Advice: Whatever you hear when you hear “neither, nor” is what you should use. Both translation schemes are logically equivalent to one another and express the exact same relationship between the two component statements. When we look at truth tables, we will be able to prove this clearly.

Material Conditional

English includes many alternative phrasings that appear to be equivalent to the material conditional. Furthermore, in English and other natural languages, the order of the conditional will sometimes be reversed. This permits speakers to vary their conditional statements with a bit of personal style and speaking preference while keeping the same meaning.

We can capture the general sense of these cases by recognizing that each of the following phrasings would be translated in the form of □→△. The most important thing to notice is the position of the antecedent in both the original English and the symbolic translation.

(In these examples, we mix English and our propositional logic, in order to illustrate the variations succinctly.)

If □, then △.

△, if □.

On the condition that □, △.

△, on the condition that □.

Given that □, △.

△, given that □.

Provided that □, △.

△, provided that □.

When □, then △.

△, when □.

□ implies △.

△ is implied by □.

□ is sufficient for △.

△ is necessary for □.

△ is a prerequisite for □.

□ guarantees that △.

The Special Case of Only

An oddity of English is that the word “only” changes the meaning of “if.” You can see this if you consider the following two sentences.

Fifi is a cat, if Fifi is a mammal.

Fifi is a cat only if Fifi is a mammal.

Suppose we know Fifi is an organism, but we don’t know what kind of organism Fifi is. Fifi could be a dog, a cat, a gray whale, a ladybug, a sponge. It seems clear that the first sentence is not necessarily true. If Fifi is a gray whale, for example, then it is true that Fifi is a mammal, but false that Fifi is a cat; so, the first sentence would be false. But the second sentence looks like it must be true (given what you and I know about cats and mammals).

We should thus be careful to recognize that “only if” does not mean the same thing as “if.” (If it did, these two sentences would have the same truth value in all situations.) In fact, it seems that “only if” can best be expressed by a conditional where the “only if” appears before the consequent (remember, the consequent is the second part of the conditional—the part that the arrow points at). Thus, sentences of this form:

□ only if △.

Only if △, □.

are best expressed by the formula

□ → △

The special case of “only if” as well as its synonyms “necessary condition” (as well as variants, “…is needed” or “…need to” etc.) can be tricky to think through. Distinguishing between “sufficient” and “necessary” conditions may also pose difficulty. So, we will find it helpful when translating to pay attention to the positions of antecedent and consequent. Just drop into those spots whatever was claimed as necessary or sufficient. Memorizing this diagram may help:

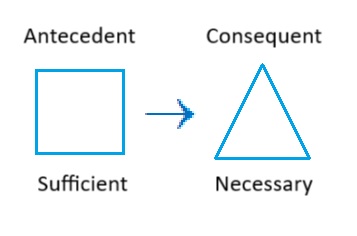
Simply put:

If something is claimed to be “sufficient,” then stick it in the antecedent.

If something is claimed to be “necessary,” then stick it in the consequent.

For example:

You need to study to do well in class.

Q: What was asserted as the thing that was needed? A: “You study.”

So just stick that claim in the consequent position (i.e., the △ spot).

W → S

When we read that back, we get something intuitive like: “If you did well in class, then you studied.” We can confidently assert this, because “you study” is a necessary condition for doing well. We would not want to say, “If you study, then you do well” (translation: S → W), because that’s false (studying is not sufficient to do well—you know, you have to also take the exams, come to class, turn in your homework on time…). More importantly, we would not want to translate our original (true) claim into something that the original speaker never said. This would be a failure of ours to listen well.

Material Biconditional

We previously noted that we don’t really need the biconditional operator. It exists to give us a useful way to communicate with precision and avoid confusion in the ways we express conditional relationships. In English we note this with how many more words it takes to express a material biconditional (and there are really only two):

□ if and only if △.

□ is a necessary and sufficient condition for △.

That’s a lot of words. Contrast these with how briefly and simply we can express the simple conditional. So, there’s a tip: if there are many more words coming out of that person’s mouth, they mean a biconditional. Simple.

Last, note that when translating from English into our symbolic language, we put the component statements in the order in which they appear in the original English. This too is very different from our translation technique when addressing a simple conditional, where the English typically flags the antecedent regardless of the order in which it was said (e.g., “I’ll get some milk, if I go to the store.”). However, with the biconditional we just translate in the order of the original English expression. Again, simple.