1 What Is Logic?

Basic Concepts

Logic: A Working Definition

Logic is the study of methods and means of evaluating arguments. Great. We have a definition in hand; now we can move on to the techniques.

Not so fast. Definitions like this are very convenient (you should memorize this one). They fit easily in the back pocket of your mind, and we can retrieve them on command at our leisure (or when the quiz question comes up). Yet in doing so we find it all too easy to repeat them mechanically and without understanding. Thus, they fail us when treated this way.

I will repeat: you should memorize this definition (as you should memorize all the definitions in this textbook). However, you should not just memorize it. A properly memorized definition is valuable because it works to organize additional concepts. A good working definition is like a paper or chapter outline: it strings together all the main components in one tidy piece of information. But make no mistake: if we have no command of those other concepts, then such a definition is empty, no matter how thoroughly memorized.

Logic is the study of methods and means of evaluating arguments. Let’s break that down. Logic is…

The Study: You will strive to learn—this is not a casual overview. This is not a movie-like experience in which you passively receive information. You will be the main mover in making this class worthwhile.

Methods and Means: There are techniques used here. These techniques distinguish a logical mind from the less-than-reasonable minds so frequently encountered. These are the nuts and bolts of our discipline, which you should learn to strengthen your mind.

Evaluating: There is a goal to logic—we judge. In the contemporary college climate, there is a bit of resistance to the very notion of judging people. Too bad. If you are not judging, you are not doing logic. How well you do it—that depends on your mastery of the methods and means.

Arguments: There is a focus to logic—we look at arguments. Of course, everyone knows what an argument is…right?

Argument: A Working Definition

We might hope that everyone knows what an argument is when they see one. Experience has shown that this is likely a foolish hope. If you think this is obvious, if you think everyone gets it, and especially if you think you do not need to work at getting better at this…well, there is that fool’s hope to cling to if you are so inclined.

Here lies the first really great task in this course of study: understanding what an argument is and how to identify one. First, a (very) rough definition:

An argument is a set of statements, some of which are intended to support another.

Let us try a quick example of what that might look like. Here’s a set of statements:

1. College can be expensive.
2. Many students do not have the money to pay for expensive books.
3. If every class requires an expensive book, it is hard for students to take a full-time load.
4. Using free textbooks helps many students.

All by themselves, we don’t really have an argument yet. We merely have a group of statements with very little structure. You could conceptualize it like this:

To the logician, there’s not much of interest here. We don’t have a sense of how this set is carved up. Yet if we frame it like this we may do better:

1. College can be expensive.
2. Many students do not have the money to pay for expensive books.
3. If every class requires an expensive book, it is hard for students to take a full-time load.

Therefore, using free textbooks helps many students.

That makes it easier to see the argument, and we can see how our current definition applies. We can see (a) the whole set, (b) the chunk of it we referred to as “some of which” now separated from the final part, (c) the remainder of the set, “another” statement. Most importantly, we can see that there is an important relationship between these two chunks. The first chunk (of three statements) was pitched with the intention of supporting the other chunk (the last statement). You can visualize an emerging structure now:

All of this is now easy to see thanks to the help of the word “therefore,” which is represented above by the three-dot symbol: ∴.

So why did this change turn the original group of statements into an argument? We’ll need to dive further into the definition of an argument to answer this.

Argument Components

In our first try at defining “argument” it may not seem like we got very far, but already we said a mouthful. Let’s break this down. An argument is…

A Set: At the most fundamental level, an argument is just a (special) collection of things. You need that collection of things to make an argument. So when you see a single thing (as in “one statement”) you should never refer to that as an argument. An argument is the whole set, and that set has special properties that a good logician will focus on. Indeed, a logician will pay more attention to the quality of the whole set than to the things most folks think are important.

Statements: Arguments are sets of statements—so we should realize that we are not talking about agendas or disagreements or fights. There is just a set of statements…with structure imposed upon it. Structure, as it turns out, is almost everything of importance.

Some of Which: In the above group of statements, we find that some of them have been given a job. They are put forth by the author of the argument to get a job done. These statements work in the service of “another” (see below). They do not work in the service of one another. This block of statements often has its own structure, but at the most basic level we treat it like a gaggle of statements all pushing towards a common goal. Or at least, they should be all pushing in this direction.

Intended: Now we come to the heart and soul of an argument: there is a special intention to accomplish a very specific thing. The author of the argument has this intention. This is what brings forth structure into their collection of statements. As it turns out, this is the key to being able to identify an argument and distinguish it from any other group of statements. We (the audience who receives the argument) seek to understand the intention of the author. Once we see that they intend to use a group of statements as workers with a job that is aimed at another statement, we get our first glimpse of their argument. Of course, merely having an intention to do something does not mean one will succeed—our intentions often lead to failure or misinterpretation. This makes identifying an argument a challenge at times.

Support: The job of the first block of statements is to “support” another statement. That is their job; that is why they were brought into view by the author of the argument. Of course, having a job to do does not mean one succeeds in doing it. Having a job just means that a role exists for those with the job. The intention of the author is to put the first block to work: the job of “support” is to establish the truth of another statement. This sort of “support” is very different from “helping to explain another statement” or “giving an example of another statement” or “being about the same topic of another statement,” etc. The meaning of “support” here is specific to truth: on the basis of the first block of statements, the truth of another is established. At least, that’s the intention.

Another: The statement that is the target of the support has no job. That is, this statement is much like one who stands on the shoulders of others who try to hold them up. Ask yourself, who supports those on the ground? The answer is: nobody. Only this statement gets the intended support. The other statements in the argument are put forth unsupported. While this statement is much like a king who sits atop others who sweat and toil to support their glory, this statement is not really doing anything in the argument. This one is merely the final takeaway in the argument. This is the one claim the author was hoping you will believe to be true because they established its truth when they presented the other statements. At least, that’s the author’s intention.

You may find it useful to picture an argument as follows:

Now we can lay on some technical terms. But first…

Quick Sidenote: Technical terminology (i.e., jargon) is common in every field and discipline. We need to get comfortable adopting such terms, because (a) it helps us communicate clearly with others, (b) it helps us keep our own thoughts precise, and (c) due to (a) and (b) it helps us avoid errors and confusion. Besides, picking up jargon can be kind of fun sometimes.

Special Sidenote: In logic, some technical jargon is adopted from everyday language. That creates a high likelihood that the new student will get confused. They will conflate what they “think” a term means in logic with what they are previously familiar with hearing. Do not do this. When you hear a term you think you know, treat that feeling of familiarity with great suspicion. Chances are good that what you think something means has little to do with how a term is used in logic.

Back to our definition: we can insert some technical language.

All we really did was add labels to the basic blocks that form the structure of an argument. We have not said anything more about these that we did not already know in the basic definition. For now, what matters is this:

There is nothing particularly special about a conclusion—it is nothing more than a statement, just like all the other statements in the argument.

There is nothing particularly special about a premise—for it too is a statement, much the same as every other statement in the argument.

The only thing that these labels do is help us keep track of the structure of the argument. And insofar as they do that, they do good work. For we need this technical language to help focus our mind while we are evaluating arguments.

Statements: A Working Definition

We know that arguments are just structured sets of statements. This definition does us little good if we do not properly understand what a “statement” is and how it differs from similar things.

In the simplest terms, a statement is simply a claim one makes about the world. You and I try to make claims about what’s happening all the time. For example, we say things like:

• The game is on TV tonight.
• We are having spaghetti for dinner.
• I’m late for class!
• My car is faster than your car.
• This class is super cool.

Notice that for each of these statements, the attempt to make a claim about the world is accountable to the world. I mean, if the game is NOT on tonight, I got something very wrong in what I was trying to claim. I failed in an important way, because I was trying to say what the world is really like.

This is very different than other things we do with language. Consider the following:

• Will you watch the game tonight?
• Pass the spaghetti please.
• Why! Why! Why do I keep getting up late?
• Jump in the car.
• Take this class.

In each of these examples, we see that the speaker is not making claims about how things are in the world. Instead, they are (a) asking for someone else to make such a claim, (b) making requests for the world to be a certain way, or (c) simply expressing frustration. There is no effort to capture the way the world is or was.

Truth Value

The point we’re making is that statements have a special quality about them. They are not simply English sentences (“sentence” is not a synonym for “statement”). Statements have a logical property we call “truth value.” Since we are just starting our path to study logic, we’ll keep this simple. For now, we will concern ourselves with only two truth values: true and false.

Statements have truth value. Questions, commands, and exclamations have no truth value. So, I can ask questions about their truth. Consider this:

“True or false: Some fleas are larger than elephants.”

You might know the answer. You might not. In any case, at least you know that the question has a sensible answer. However, not every true/false question does, and there’s a good reason for this.

Now consider how you would respond if I asked:

“True or false: Will you have spaghetti for dinner tonight?”

What if I asked this:

“True or false: Dogs?”

If you are confused by these last two “true/false” questions, good! That is pretty much the correct response. These things don’t have a truth value. Only statements have truth value.

So now you know how to respond the next time someone asks: “True or false: Dogs?” The question makes no sense, because nouns have no truth value. Questions have no truth value. Requests have no truth value. Exclamations have no truth value. Only statements have truth value.

Let’s get back to truth value itself. Some advanced systems of logic use more than two truth values, but for now the most intuitive starting point is to use just two: true and false. I say “intuitive” because most of us have a pretty good idea of what these mean (at least good enough to get us started).

That’s going to work very well for us for a very long time. Besides, most people already walk around with this understanding in their mind.

As easily as this begins, there is no shortage of folks who claim to be confused about what is true and who gets to say that with any sort of authority. I suspect this is due to two confusions:

• Word games/misunderstanding what is meant by a word or a term
• Conflating truth value with facts

To the first confusion, we should make it a healthy practice of ours to ask for clarification when someone says something we think is wrong or does not make sense. All too often we get into unnecessary disputes when one person supposedly disagrees with another, only later to realize that they did not know what the other person was really saying. The imagined dispute over what is true or false ends up having nothing to do at all with truth value—it boils down to missing the reference of what was being said all along.

Reference

When we talk about “reference” in a statement, we are talking about what the statement is about. In short, the reference of a statement is its subject. In this sense, statements pick out a small bit of the world and try to describe it or its relation to other things. So, consider the following statements:

• The dog is sleeping.
• Aunt Sally makes great pecan pie.
• When you go to the store you always forget your shopping list.
• The housing market today is good for new homeowners.

In each statement, we should be able to find the thing that the statement picks out. This is what the statement refers to as it attempts to describe the world. The wakefulness of the cat or the hamster is not being described in the first statement—it is “the dog” which is pointed to and identified as the focal point of the description.

When folks disagree about what is being pointed to in a statement (e.g., is it “this dog Fido” or “that dog Spike” the speaker intended?), and they don’t notice they are talking about different subjects, they often say they disagree on the truth of a statement (or worse, that truth is relative). In these cases, we should see that they do not disagree on truth at all. Rather, they disagree on which statement is being evaluated in the first place. A simple clarification would dispel the alleged dispute: I didn’t say “Spike is sleeping,” I said, “Fido is sleeping.” Thus, the value of proper names should come into sharp focus here. Proper names are not always necessary, but crisp use of language makes the subject of our claims clear and helps everyone involved.

Facts of the World and Truth

To the second confusion, we should remember that only statements have truth value. The world does not have truth value—the world be whatever the world be, and those are the facts. If we distinguish between truth and facts, then we easily see that people can have legitimate disputes over how to properly make claims about the world, but they cannot dispute the facts of the world. If we look carefully, we see that so-called disputes about the facts are really just disputes about our claims of those facts. The facts are the very thing that help us judge between which claims are correct and which are not.

However much differing beliefs and claims may tear us apart, facts bind us together: they form a common point of reference we all share. We hold ourselves accountable to the facts in our efforts to make truthful claims.

Compound Statements

Before we leave statements, we will point out one more thing. Remember when we said that “sentence” is not a synonym for “statement”? This is important, as we will quickly see that many sentences contain multiple statements. Consider:

School can be challenging sometimes, but I am either up to the task or I will seek help when I need it.

If you go to the movie, you should not eat the popcorn nor pay for that overpriced drink.

Mike and Sally will sing in the play.

These are all complete single sentences. Each of these contains multiple statements. The speaker put smaller statements into certain relationships with other smaller statements to make a larger statement. When a speaker makes statements like these, we call them compound statements.

Notice that to construct these compound statements, a speaker must do more than keep talking. The speaker must put smaller statements into logical relationships with other statements. When we speak out loud such relationships, we use key terms that express our intention. We need special words to set up these relationships in our statements.

Small words like “and,” “if,” and “or” do big work. These terms set up logical relationships, and in doing so, they establish the meaning of compound statements. That’s huge! Unfortunately, people often fail to pay close attention to these important elements of compound statements. When they make this kind of mistake, they literally do not understand what the speaker is saying. Logicians try to avoid this error by focusing keenly on these tiny words. Later we will cover several techniques to pay very close attention to how these statements are constructed.

The Inference: A Working Definition

When we say that there is structure in a set of statements, we have seen that this comes from the intention of the author of the argument. The content of that intention (i.e., what is intended) is understood as “to support for the truth” of the conclusion.

Here’s another way to look at the same intention: the author intends to use claims to support the truth of a statement.

You can visualize it this way:

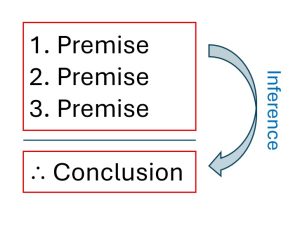
Here’s an example.

Let’s say I tell you two things:

1. “Students who register for Mr. Marshall’s class tend to get As.”
2. “You need an A this semester.”

Let that sit for a bit.

STOP! Before you go further, try reading the two statements again.

Q: Where does your mind go?

Chances are high that on the basis of those two statements your mind leapt to another statement:

“I should register for Mr. Marshall’s class.”

You might have doubts about the truth of the first two statements. But if you considered what the first two were stating, there’s a good chance your mind leapt to this third statement anyway. That is, you inferred this on the basis of the other two statements.

NOTE: You did not “assume” you should register for that class—you INFERRED this on the basis of those statements. The idea that you should do so did not just pop into your mind with no basis.

Nor did this come to mind simply because you wanted it to be true or you hoped it would be true. Your mind did not make a leap of faith. We often misuse language in this way to say that what you now believe was simply “assumed,” but that undersells your mind. Your mind leapt to this claim from the other two claims. An inference is not an assumption.

To be clear, whether or not your mind leaps from claims in reliable ways or leaps in wild flights of fancy is another matter altogether. Indeed, the study of logic is precisely the study of how to evaluate such leaps of the mind. The point is that our mind is active: it is not simply populated with beliefs, it is doing things with relationships between these beliefs.

Approaching Arguments

Up to now we have spent quite a bit of time trying to unpack the most basic nuts and bolts of what makes up an argument. Hopefully we have a better understanding of these components. Yet this does not guarantee that when we see an argument, we will be able to recognize that we are looking at one. This takes practice.

Our practice will be sped up by following a logician’s order of inquiry. On a daily basis we encounter lots of things being said—we hear lots of statements. In the mix of all that, we hear a lot of arguments. While this may be so, we often hear them without realizing that we are hearing them. In short, we miss them. Yet this is better than the alternative: for it is far worse when we hear a fictitious argument, one that was not made but we thought it was made. See…this really does require practice.

A logician approaches a set of statements with a series of questions. First up: is there a special intention here? If not, move along…nothing much to see here. There are many times when we are just encountering a bunch of statements without any interesting structure.

If there is suspicion that we are running into a special intention, then the logician may first test their own uptake of the argument.

Often, we only suspect that we see an argument, because we only suspect that we know what the author’s conclusion is in their statements. This is fine. Do not think that you have to automatically get it, like you were born with some kind of logician’s magic. If you have confusion or uncertainty, it does not mean that you were not born with the logician’s magic touch. With practice, we can grow.

When you suspect you know what the conclusion is in a set of statements, test your candidate for the conclusion. Ask yourself a question:

Does it look like the author is trying to use the rest of the statements here to establish the truth of this candidate-conclusion?

Maybe you start to feel your stomach sink. You get your answer to this question, and you feel like “no, they don’t seem to be trying to do this.” In this case, your candidate-conclusion fails the test. That’s okay. You may try another candidate.

Of course, you may also decide that there are no viable candidate-conclusions left and your suspicion about the passage was wrong: it is not an argument after all. Then again, you may find that the answer is “yes, the author seems to want to tell me the rest of the things that were said in order to establish the truth of this candidate-conclusion.” If so, then you have a strong case for thinking this is indeed an argument.

There is nothing automatic about this; there is nothing intuitive about it. We work the process through careful use of questions that help us identify the author’s intention.

There is another way to approach this test of a candidate-conclusion. Ask yourself:

When I look at this candidate-conclusion, why should I believe it is true?

If the rest of what the author said seems to be trying to answer your question, then it gives evidence that this is indeed the conclusion, and this is indeed an argument. However, if the rest of what the author said does not seem to make the effort to answer, “Why should I believe this is true?” then you should back away from your suspicion.

Examples

Identify which of the following are arguments and which are not:

1. Strawberry ice cream combines the sweet, refreshing taste of real strawberries with a creamy texture, making it both delicious and slightly healthier than other flavors. Its vibrant color and nostalgic appeal add to its charm, making it a perfect treat for any occasion.
2. I think we should make a bird house. Making a bird house supports local wildlife, provides shelter for birds, and allows you to enjoy birdwatching right in your backyard. It’s a fun, educational project that benefits both nature and your home environment.
3. Getting adequate sleep every night boosts your overall health, improves cognitive function, and enhances mood, ensuring you perform your best each day.
4. Riding a horse offers excellent exercise, improves balance and coordination, and provides a unique, enjoyable connection with nature and the animal. I’m glad to see Mary take up this hobby. She’s making a good choice.
5. Turtles make good children’s pets because they are low-maintenance, quiet, and can teach kids responsibility and patience through their care.
6. Look man, dogs are totally smarter than cats. Haven’t you seen them? They understand more commands, perform complex tasks, and exhibit strong problem-solving skills due to their social nature and trainability. This is a no-brainer!
7. Watch Mike hit this ball. He’s the best.
8. Recycling clothes reduces waste, conserves resources, and promotes sustainability, helping to protect the environment and reduce landfill usage.
9. They say voting is important for you. They say it empowers citizens to influence government decisions. They say it protects your rights. But all these politicians care about are your votes. None of these things is actually true.
10. ChatGPT can make mistakes due to limitations in understanding context, nuances, or up-to-date information, as well as the inherent challenges in natural language processing. You are just as likely to get a wrong answer from Chat as you are if you just took an educated guess. So, you should do your own work and make better-than-educated-guesses to answer questions.

Help and Challenges in Identifying Arguments

Illatives and Implicit Statements

Note that in the preceding examples, some terms may have helped you identify the intention of the author. We call these terms “illative” terms, which simply means they are flags that help identify an inference. Authors do not always use an illative term to signal their intention, but it sure helps when they do. For example,

So, (fill in the blank with a conclusion).

(fill in the blank with a conclusion), because (fill in the blank with a premise).

Thus, (fill in the blank with a conclusion).

Therefore, (fill in the blank with a conclusion).

Hence, (fill in the blank with a conclusion).

Consequently, (fill in the blank with a conclusion).

These terms make it pretty clear that the author wants you to believe in what they said precisely because they said other things they hope you accept. However, many times an author will use tone of voice, intonation, or other casual phrases to indicate their conclusions. Language is complex.

Indeed, things can get really tricky when an author intends to say something but does not say it out loud. That is, we often hear an author say something and know that they also meant to say something else along with it—they just didn’t. These are implicit statements.

Identifying an implicit statement can be very difficult, and so it often gets us into trouble. We might be accused of putting words in the mouths of others.

“I didn’t say that!”

“Yeah, but it sounded like you were saying that…”

Yeah. This is going to be a long night.

Logicians should be somewhat loath to claim someone is making an implicit statement. At the very least, you should be very careful and conservative in claiming that someone intended an implicit statement to be part of what they were saying.

The definition tells us we should “charitably and reasonably” be able to attribute the unspoken statement to the author. To be “charitable” we need to understand that the author may want to have included the statement but just couldn’t or didn’t have time, and so forth. So that rules out things like: “You hate my mother!” This is not likely something someone wants to say. That’s just looking for a fight.

To be “reasonable” we need to consider the broad context of the statements. This is the really hard part. I might be able to imagine a scenario where the author could have intended to include a statement. This is actually very easy—and this is why we are rightly accused of putting words into someone’s mouth. Do not do this. Imagination is not the same as reasonable judgment.

The fact that you can imagine an intention does not mean the author intended it. You are accountable to the author’s words. If the words (or the actual context in which they are delivered) warrant claiming that there is enough context supplied, then we can cautiously include the implicit statement. However, if the words (or actual context) do not supply that context, our imagination is not a suitable substitute.

Consider two of our previous examples:

“Getting adequate sleep every night boosts your overall health, improves cognitive function, and enhances mood, ensuring you perform your best each day.”

“Recycling clothes reduces waste, conserves resources, and promotes sustainability, helping to protect the environment and reduce landfill usage.”

Neither one of these are arguments. However, many folks may think “hey, I can see how someone might argue for this…” In proceeding this way, we are using our imagination to override the author’s actual words.

In the first, we might imagine a situation in which someone would say this in order to support a conclusion (something like: “You should get adequate sleep”). However, look at the passage again. Is there anything provided that tells us clearly that the author wants us to believe it is true that we should get adequate sleep? No. The author is just telling us the benefits of adequate sleep. This would likely appear in an argument with that conclusion, but nothing in the passage itself suggests that such an argument is being made. This is just a statement about the benefits of adequate sleep.

In the second, we might see even more clearly that this is just a statement about the benefits of recycling clothes. We can easily imagine a scenario in which a friend is trying to convince us it is true that “We should recycle our clothes.” However, that imagined scenario is not what is directly in front of us. The words directly in front of us could just as easily be nothing more than an explanation of benefits. As audience members, we have to push this into an intention that we fabricated. The author’s words alone don’t give us enough evidence to make this judgment about their intention.

Consider another example from above:

“They say voting is important for you. They say it empowers citizens to influence government decisions. They say it protects your rights. But all these politicians care about are your votes. None of these things is actually true.”

Here we have an argument, and we have a good bead on the conclusion: “All these politicians care about are your votes.” However, to really understand what the author intends, we will find it helpful to understand an important implicit statement in the passage. We should pick up on something like:

“Politicians are lying to you.”

We might even think this is likely included in the author’s argument:

“Politicians know these things are not true.”

Unlike the other examples about sleep and recycling clothes, we do have something in front of us to point to when we say the author likely intends to include these in their statements. The repeated and italicized phrase “they say…” strongly suggests that the author wants us to understand that there is something suspect about what these people say. This amounts to an important premise in their argument. We are not using our imagination here to concoct some story about the author’s intentions. We are looking directly at what they say and how they say it.

Given that the examples in this textbook are always provided out of context, you need to be able to point to specific aspects of the black-and-white text to make a claim for an implicit statement. However, in real life you often have the benefit of a live environment as well as the overall context of an extended conversation to provide additional support. The moral remains the same:

Be very careful and cautious in claiming that someone intended an implicit statement, and be on guard against putting words in people’s mouths.

Logical Properties of Arguments

Validity: A Working Definition

Once we know that we are faced with an argument, we can begin our evaluation of it. Note that when faced with an argument, most people will not evaluate the argument. Most people will simply evaluate the individual statements that make up the argument. Most people are not well trained.

Logicians do not judge individual statements first: they look to the relationship between the premises and the conclusion. They do not look at the statements as much as they look at the spaces between the statements (more importantly, the space between one chunk of the set of statements, the premises, and the other chunk, the conclusion).

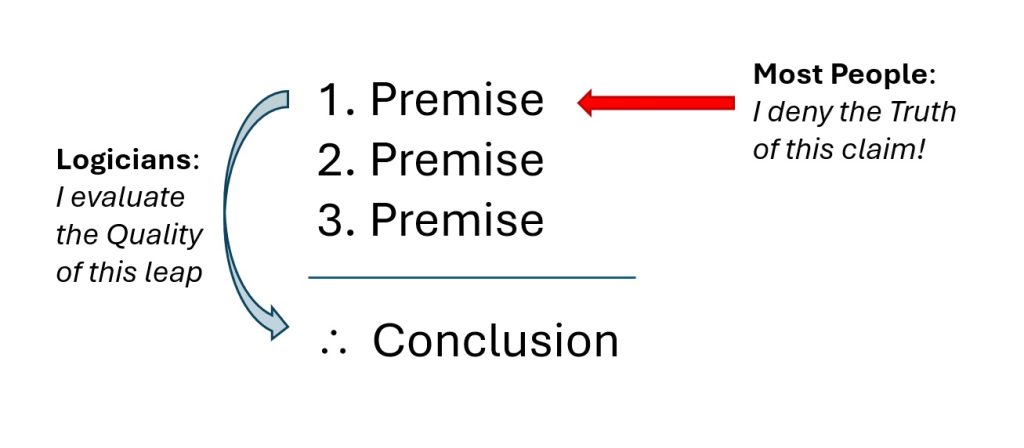
The first concern to the logician is a key property of arguments: formal validity. This is a property of arguments—this is not a property of statements. So it makes no sense to talk of “a valid statement” nor “a valid point” made in an argument. Only an argument as a whole has this property.

The concept of formal validity is often misunderstood in large part because it means less than we think it means. So let’s go slow.

That’s not pretty. This account is awkward and lacks a graceful flow, but it works very well to help us avoid confusion. Of course, there are other ways to define validity correctly. However, these ways often mislead students into thinking validity is a robust concept…one familiar to their everyday preconceptions about validity. That is why we will not use these other definitions.

Let’s try a simple example:

1. Mike and Larry will go to the football game.
2. Jane and Shauna will go to the football game.

So, Mike and Shauna will go to the football game.

Ask yourself: Are you sure that Mike and Larry will go to the football game? You probably don’t want to bet the house on that claim. After all, that single claim could be false. So you probably don’t want to bet that the conclusion is definitely true. However, this is not what is at stake when we ask if this argument is valid.

When we ask if this argument is valid, we just want to know if it is possible that you could say both premises are true and then deny that the conclusion is true. So…can you deny that the conclusion is true if both premises are true?

A: No (and if you think you can deny this, read the example again).

The punchline here is that we can see how we must accept the truth of the conclusion if both of those premises are true. So being able to give a valid argument is generally a good thing.

Going back to our ugly definition, the first thing we should notice about this definition is that it is framed in terms of a negation.

An argument is valid if it is not…

So, in this account the concept of formal validity is a kind of denial. When an argument is formally valid, we know for sure that something is NOT the case. Be very careful with how you think of things that are denied. Ask yourself:

Q: When you know that something is not the case, what else do you know?

For example, remember when you were younger, and you had to check in with your mom to let her know where you were hanging out? You told her the truth! (You would never lie to your mother…) You truthfully told her:

No Mom, I’m NOT at little Timmy’s house. (She never liked Timmy anyhow.)

As a good and honest child, you spoke truthfully. Then again, in possessing this truth, what did Mom really know? Did Mom know where you actually were or just where you definitely could not be found?

A: Momma knew very little about your actual whereabouts.

(…and you probably knew this, which is why you told her the truth this way…)

The same is true of formal validity. When an argument is valid, you know that something is definitely not the case, but you do not know what definitely is the case. You know very little about the argument. So don’t get your hopes up for this concept; it is a thin concept with very little substance.

We cannot say a valid argument has a true conclusion, we cannot say a valid argument has true premises, we cannot deny that the statements are all false, we cannot insist on much of anything.

What we can say is that there is a kind of guarantee in a valid argument: the guarantee is that one thing in particular is not possible. Put differently, there is a specific combination of truth values that will never appear. Namely: all true premises and a false conclusion.

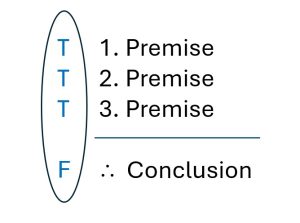
For a valid argument, you will NEVER see that happen. So you can visualize it like this:

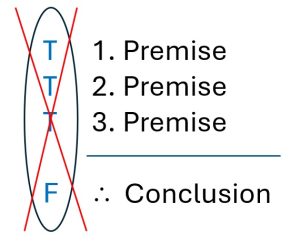
Ask yourself: If I know that this combination of truth values will never appear, what combination of truth values does appear?

Like Mom, you cannot say. You do not know much of anything about the truth values in a valid argument. All you can say with certainty is that “T, T, T / therefore F” will never be the case. Still, this is valuable information. After all, as we saw above, if it turns out that the premises are indeed all true, then you know something important about the truth value of the conclusion: it must also be true. So, we can now safely say that another way to define validity is as follows:

In saying this, we are not saying that the premises are actually true; we are simply saying that IF they are all true, this will lock in the truth of the conclusion.^[1]

Identifying Validity

One of the easier ways to test for validity is to resist the temptation to attack individual statements in the argument. We want to know if something is not possible. Specifically, we want to know if the union of two things is not possible. We want to know if we can deny the possibility that these two things coexist:

(a) all the premises are true

AND

(b) the conclusion is false

Is this union of (a) and (b) impossible?

We do not (yet) want to know what is actually the case, just what is not possible. The simple way to test for this is to accept half of what is denied and see if we can make the other half feasible. This is what it looks like:

1. Accept the (a) part: treat all the premises as if they are true
2. Now see if you must accept the (b) part (while still holding on to the (a) part)
3. Ask yourself: If one really believed all of (a), is there any way to avoid accepting (b)?

This test reveals if you must accept the truth of the conclusion under the truth of the premises.

Invalidity: A Working Definition

Validity is an all or nothing thing. If an argument is not valid, then it is invalid. But what does that mean?

Notice first that the definition of invalidity is almost the exact same as that of validity. This is because they are sister-concepts (two sides of the same coin). All we are inquiring into is whether or not a certain possibility exists—the same possibility is highlighted in each definition. Thus, our definitions are worded in almost exactly the same way. The only difference is whether it is or is not possible for that specific combination of truth values to happen.

Logical Categories of Argument Types

We have seen that once logicians know they have an argument in front of them, they approach it with a basic question. Is something possible or not? Once they have answered that, they know if the argument is formally valid or invalid. However, the logician’s inquiry does not stop here.

Logicians systematically continue their inquiry based on the answers given to previous questions. We will do well to try to discipline our minds in this way. Logicians do not rush forward agreeing or disagreeing with the truth of the conclusion. After all, this is something anybody can do and shows no real skill at evaluating arguments. Rather, the logician will carefully look into the relationships that help us understand the quality of reasoning in the argument.

Soundness

Say we discover this about a given argument: No, it is not possible for all the premises to be true and the conclusion false. Now what question comes to mind? You are not alone if now you start to wonder: Well, are all the premises in fact true?

The answer to this question is now important to us. After all:

• If they are all true, we have to accept the truth of the conclusion.
• If they are not all true (which means at least one of them is false), then we are not forced to accept the truth of the conclusion.

Put differently, we see that there is a lot on the line now in whether or not all those premises are true. This is the logical force of a valid argument. Not surprisingly, this is also why many folks are so keen to poke holes in the truth of a premise. For if they can find fault in just one of the premises, they take all the wind out of the logical force behind the argument.

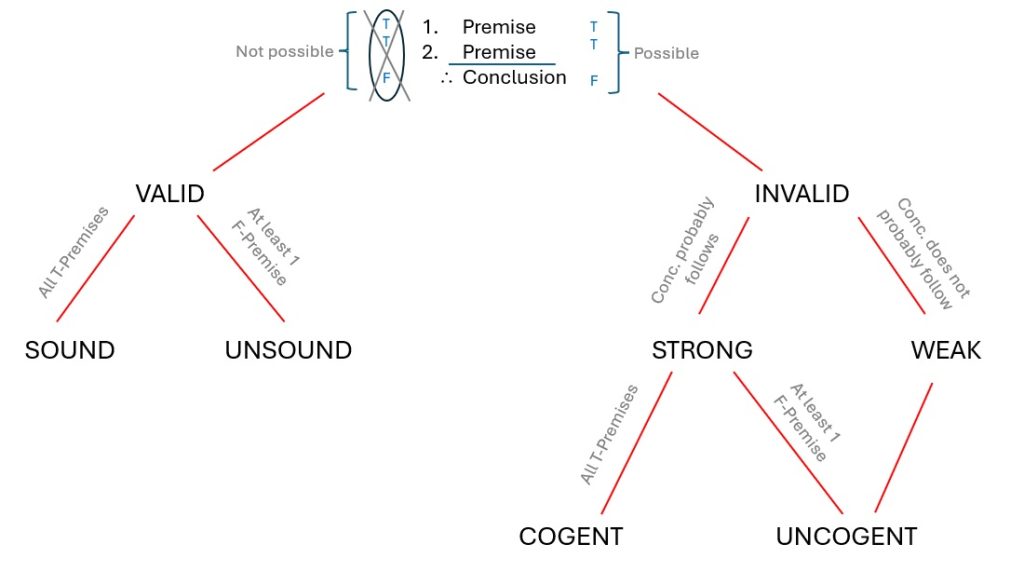
Logicians have special names for arguments that have these qualities. So if we already know an argument is valid, then we can say of the two options above that an argument is:

Sound: when it is valid and all the premises are true

Unsound: when it is valid and at least one of the premises is false

All things being equal, we regard the Sound Argument as our gold standard for quality in an argument. These are very powerful arguments that force all rational people to accept the truth of their conclusions. They are also very rare and hard to produce.

Strength and Weakness

Most of the time when the logician asks the first question of possibility, the answer reveals that an argument is formally invalid. This is not a death sentence for the argument. This does not mean that the argument is “bad” nor that we might not seriously entertain it. Indeed, the logician continues to consider and evaluate it. We might still have a pretty good argument in front of us.

So, a new question comes to mind when we know the following: Yes, it is possible for all the premises to be true and the conclusion false. The question is no longer of possibility but of probability.

Q: How probable is it that the conclusion follows from the truth of the premises?

Notice, we have already accepted that it is possible for the conclusion to be false (even if all the premises are true). But how likely is that? If it is not likely it will be false, then the conclusion probably follows from the truth of the premises. Let’s face it, that’s not bad. Absolute certainty is tough to come by these days. Having a high degree of probability is not as good, but it would be nearly as nice.

Arguments that are invalid are met with the question of probability. The result of our question leads to the following classification of invalid arguments:

Strong: an invalid argument in which the conclusion probably follows from the truth of the premises

Weak: an invalid argument in which the conclusion does not probably follow from the truth of the premises

To understand “probably” and “not probably,” we can consider the percentage of likelihood. Anything that is 50% likely or worse is “not probable.” Anything above 50% (even just a little, like 50.2%) can be said to be probable.

In practice, we often do not get firm percentage figures in an argument. More often than not, people will present arguments with indicators of probability. For example,

1. Most people who exercise daily live longer.
2. Mike exercises daily.

Therefore, Mike will live longer.

The term “most” is not as precise as 98%, however, we get ample sense of the probability that the conclusion follows from the truth of the premises. That is, assuming that the premises are true, we can say that the conclusion probably follows. We don’t know that the premises are true simply because we know that the argument is strong.

We should note something similar and something different here from our discussion of validity/invalidity. The similarity is that in stating any of these, we do not also state that we know the truth value of any of the premises. The difference is that unlike validity/invalidity (which is an all-or-nothing property), strength and weakness in an argument admit of degrees. Like physical strength and weakness, the strength and weakness of an invalid argument vary a great deal. You might be strong but admit that there are folks stronger than you. You might be weak but admit that you are not the weakest kid on the block. All forms of strength and weakness come in degrees.

Cogency

If we know that an argument is strong, we have some assurance in the logical force of the relationship between premises and conclusion. We are not 100% confident, but we are well assured…that is, if the premises are all true. Now a familiar question should come back into view.

Q: Are all the premises true?

If the answer is yes, then we know we should probably accept the truth of the conclusion. In such a case the argument retains quite a bit of logical force. So, we classify these as such:

Cogent: an invalid argument in which the argument is strong and all the premises are true.

Uncogent: an invalid argument in which the argument is strong and at least one premise is false.

Similar to an unsound argument, when we learn that an argument is uncogent, it has lost much of the assurance that we were looking for in a quality argument. Our confidence that the conclusion is true is undermined, and the argument no longer appeals to our rational nature.

Additionally, we will regard all weak arguments as uncogent. This is in large part because they also lack all logical force regardless of the truth of their premises (because we cannot say that the conclusion follows even if all the premises are true). Weak arguments are pretty much worthless.

Arguing Well (or, Backing Out of an Argument without Backing Down)

Let’s go back to the beginning. If we want to mount a quality argument, we are probably going to try to make a sound argument. Yet we know that this is difficult to do. Often someone points out that we cannot really maintain the truth of all of our premises—they “poke holes” in one or more of our premises. Having an unsound argument is less than ideal, because we know that the audience does not have to accept our conclusion.

So do we give up? No! We fight back. This is an example of how it usually goes:

Jeanine: “Listen Bob, you should register for Mr. Marshall’s history class. Everybody gets an A! You take his class. You get an A.”

Bob: “Hold up. What about our buddy David? David took Mr. Marshall’s class, and he didn’t get an A.”

Pause: Jeanine’s argument is a bit more complicated in structure than it first appears. We’ll look at that later. For now, here’s the format of Jeanine’s argument that concerns us.

1. Everybody who takes Mr. Marshall’s history class gets an A.
2. You take Mr. Marshall’s history class.

Therefore, you will get an A in his class.

Bob has picked up on this argument and found an error in the first premise. Bob found a counterexample to refute Jeanine’s key premise. Will Jeanine give up? Not likely.

Jeanine: “Okay, fair enough, but we both know David’s not the most serious student. Almost everyone who takes Mr. Marshall’s class gets an A. Take the class. Boom! You’ll get an A!”

Bob: “Well, what about Hank? Hank took Mr. Marshall’s class and he didn’t get an A either.”

Pause: Notice that Jeanine backed out of the attempt to construct a valid argument. Her strategy shifted and now she is intentionally constructing an invalid argument. However, Jeanine wants to make it as strong as possible.

Unfortunately, Bob has again found an error in Jeanine’s key premise. Bob is chipping away at Jeanine’s ability to maintain that all the premises are true. Does Jeanine give up? Again, not likely.

Jeanine: “Okay, okay. We don’t hang out with the sharpest crowd. But that’s not you, Bob. Most people who take Mr. Marshall’s class pass with an A. Take the class. You’ll get an A!”

Bob: “You’re right. I’ll probably get an A.”

Pause: Notice that Jeanine softened the key premise from “almost everyone” to simply “most.” If Bob kept pushing with counterexamples, this may have been softened even more (e.g., “better than half…”). However, Jeanine also squeezed Bob into the group of “most” by insisting that he is not like those others who fall in the class of Bob’s counterexamples. This left Bob with good reason to accept the truth of the conclusion. Bob is not guaranteed to get an A, but if Jeanine is right about what is claimed in the premises, Bob will likely get an A.

Side Note on Inductive vs Deductive Arguments

Arguments that are invalid are evaluated using inductive standards of reasoning. We will look more closely at inductive arguments in later chapters.

Logical Properties of Related Entities

Now that we have seen how arguments with different qualities can be classified, we can look at other logical properties that interest logicians.

Statements

Statements can be classified according to important possibilities tied to their truth value. Three classifications are worth noting: logical truth, logical falsehood, and logical contingency.

We’ll start with the first of these.

Logical Truth

Since we only have two truth values (true and false), if it is not possible for a statement to be false, then we can say it is always true. Notice how different this is from saying that a statement is merely true. “The student is reading” is a true statement. However, I could not say that it is not possible for that statement to be false. Clearly, that statement can be false; it is merely true right now (assuming our reader is a student). So a logically true statement is very special. Here’s a cheap and easy example:

“The lights are on, or they are not on.”

Clearly, that statement will be true no matter what the state of the lights is right now (or ever).

Logical Falsehood

Chances are that some of you reading can suss out the definition of a logically false statement. Give it a try before reading further…

As before, since there are only two truth values, such statements are always false. Again, such statements are pretty rare and unusual. Another cheap and easy example:

“The lights are on, and they are not on.”

Again, this example makes it easy to see that no matter what is going on with the lights, this statement will incorrectly describe them. There are far more interesting and complicated logically false and logically true statements. Unlike these examples, many are hard to identify at first glance. Later we will develop tools to evaluate statements to determine if they have these qualities.

Logical Contingency

Most statements that we encounter are not like logically true and logically false statements. These are logically contingent statements.

These are what we expect of statements. Sometimes it is true that the student is reading and sometimes it is false that the student is reading. Different conditions yield different truth values. This is part of where they get the names “contingent” and “indeterminate.” The truth value of such statements is “contingent” (i.e., dependent on the state of the world). We can also say that unlike logically true and logically false statements whose truth value is fully determined by their own nature, the truth value of logically contingent statements is not-yet-determined by their own form.

Sets of Statements

Often logicians find it useful to understand the logical properties of a set of statements that is not an argument (or is not treated as such). Sometimes you just want to understand a group of statements as simply a group (without a specific structure).

Logical Equivalence

The smallest such group is a pair of statements. We sometimes find that two statements seem to track one another in their truth value. We call these statements logically equivalent.

In an equivalent pair, when one statement is true, the other one is true. The same holds for when one is false—the other will be false. They never have different truth values.

This is not to say that one (and the other) must have this or that specific truth value. So do not make the mistake of thinking only contingent statements can be logically equivalent. After all, two logically true statements will always have the same truth value. Put differently, it is not possible for two logically true statements to have different truth values under the same conditions (because under all conditions they have the same truth value). So any logically true statement is logically equivalent to every other logically true statement. The same holds for logically false statements. While this is easy to see, when it comes to two logically contingent statements, figuring out if they are logically equivalent can be more challenging. For example, consider these two statements:

The door is open.

It is not the case that the door is not open.

Those statements are probably not too hard to identify as logically equivalent. In a sense, the two negations of the second statement cancel each other out and leave us with the same meaning as the first statement. Now consider these two statements:

If the dog is asleep, the cat will come inside.

Either the dog is not asleep, or the cat will come inside.

These two statements are also logically equivalent. A little bit of thought will reveal this, but it is not as obvious as the first example. Later we will develop tools to help us identify logically equivalent statements easily, even when they are quite complex.

Logical Consistency

When we look at larger sets of statements, we often want to answer an important question:

Q: Is it possible that all those statements can be true?

We might ask this question even when we are not looking at an argument. Then again, we might ask this question when we are looking at only part of an argument (for example, when we are looking only at the premises). This is a question of consistency.

The main thing to notice in this definition is that we are asking if a specific truth value is possible for all the statements—we are not asking if the truth value is merely “the same” for all the statements. We want to know specifically if they can all be true under the same conditions.

Logical Inconsistency

The savvy student may be able to suss out the definition of logical inconsistency. Give it a try.

You may notice that this is the second of our sister concepts. We previously noted that validity and invalidity were like two sides of the same coin. Thus, their definitions were almost exactly the same. The one thing that is at stake there was whether something is or is not possible. The same holds here.

Notice two important things:

1. The definition changes and hangs on just one thing: possibility or impossibility
2. There is absolutely no mention of the word “false” in the definition

The first definition (of consistency) makes no mention of the word “false” and so this definition (of inconsistency) makes no mention of it either. We don’t care if it is possible for all statements in a set to be false. That’s not helpful, that’s just a sad state of affairs.

What is helpful is knowing if it is possible that, in some state of affairs, all the statements can be true. If yes, then it is a consistent set. If no, then it is an inconsistent set.

For example, consider this set of statements:

The lights are on.

The door is closed.

Class is in session.

Three statements are in our set. Are they currently all true? Who cares—that’s a trivial fact. What matters is if it is possible that all three of these statements can be true. That’s what matters.

In this example, the answer is yes. So we know that the set is consistent (not “the same,” but consistent). Now consider this set:

George Washington was Russian.

The moon is smaller than the state of Virginia.

Dogs walk on two legs.

We should see that all of these statements are clearly false. So what does that tell us?

A: Nothing.

Knowing that all three statements are indeed false tells us nothing about the set. We want to know if it is possible that all three statements could be true under some state of affairs.

So, might it not be possible that Washington was in fact Russian? Couldn’t the moon be super tiny (in moon-terms)? And have you never seen those circus dogs trained to walk on two legs? Could it not be the case that every dog regularly walks as they do? We should be able to see that even though these three statements are false under the current conditions of the world, it is possible that they could all be true. Thus, this is a consistent set of statements.

Now consider this set:

The lights are on.

The door is closed.

The lights are not on.

Immediately, we should be able to tell that there is no way, under any conditions at all, for these three statements to be true at the same time. At least one will always end up false.

This example should be easy, but in many cases we may find it difficult to determine if the set of statements is or is not consistent. However, as with the other logical properties, later we will develop tools that help us determine this with considerable ease and accuracy.