B. Units and unit conversions

When describing a physical property, a unit of measure is typically required. A unit gives a sense of perspective or scale relating to the magnitude of the value. To give an example: say you want to determine what to wear outside. You ask for the temperature and are told that the temperature is 10. Is that hot, cold, or somewhere in between? Without a unit to tell you the value of that number, it is meaningless. It is likely to be either 10 Celsius or 10 Fahrenheit (the most common units used to describe temperature), but those two values would require very different wardrobes when going outside!

In fact, many scientific units are given precise definitions that have to do with fundamental properties of our universe. This is to remove any extraneous errors that could result due to differences in definitions or in the measurement techniques used to determine the exact “value” of each unit. We could also consider that our definitions of units could be used by people (or hypothetical aliens from other planets) who don’t know what a term such as “gram” or “kilometer” means, but could deduce those values from an understanding of the fundamental properties of the universe.

It is important to note that two quantities with different units cannot be combined together using addition or subtraction. (A common phrase used by physics professors is that “you can’t add apples to oranges,” as both quantities are fundamentally different.) For example, it would be meaningless to add 5 meters to 8 kilograms.

It is possible to add (or subtract) two quantities that measure the same property (such as length), however, the units have to be the same. For example, adding 5 meters to 8 kilometers requires that one of the two units be converted to the other. (Either convert 5 meters to kilometers, and add to 8, or convert 8 kilometers to meters, and add to 5.)

Unit conventions

Historically, many different units have been developed to define quantities such as length, weight (force), and time. Today, while there are regional differences in the units used for many properties (speed, length, and mass), there are other properties that have units which are relatively standard across the globe. For example, modern units used with electricity such as the ampere, coulomb, and volt are part of the SI system of units and are used internationally, even in the United States.

United States customary units

The United States is one of a very small number of countries on the planet that does not primarily use a metric system of units. Many of the units used in the US are derived from British imperial units (the two unit systems are very similar although there are notable differences, including the definition of a fluid ounce used to measure volume).

Commonly used US customary units include:

  • inch, foot, and mile (distance);
  • teaspoon, tablespoon, cup, pint, quart, and gallon (fluid volume);
  • ounce, pound, and ton (weight); and
  • degree Fahrenheit (temperature).

Metric system

A metric system is simply a system of units that uses powers of ten to define units. United States customary units are not considered metric. This is because, for example, there are 12 inches in a foot, 3 feet in a yard, and 1760 yards in a mile. None of these values are powers of ten. However, there are 1000 millimeters in a meter, 1000 meters in a kilometer, and so on. These are all based on powers of ten. The SI system of units (described below) is considered a metric system, as it has units that use powers of ten.

The international standard of units (SI)

The international standard of units (SI) is the modern system of units, and is considered a metric system as it is composed of units that are based on powers of ten. This system of units uses base units (described below) that are explained by physical properties of our universe (such as the speed of light in a vacuum, a value that does not change regardless of one’s position or motion in the universe) to derive units for other physical properties. The SI system of units is the established standard used in scientific fields (even in the United States).

SI base units

There are seven units in the SI system that can be used to derive every other unit in the system. These seven units are known as SI base units. The SI base units are defined in the table below.

symbol

name

measurement

s

second

time

m

meter

length

kg

kilogram

mass

A

ampere

electrical current

K

kelvin

temperature

mol

mole

quantity of a substance

cd

candela

luminous intensity

Each of these base units has a scientific explanation that uses fundamental properties of our universe to define it. For example, the base unit of second is defined with respect to the frequency of light emitted in a particular electron transition in a cesium-133 atom. Regardless of the person who measures that frequency, an identical description of the unit of second should result.

Historically, many units were justified by a physical item. For example, there was an object formulated to have a mass of exactly one kilogram, used as a reference to calibrate precise scientific measurement tools. “The” kilogram (along with several reference copies) was preserved in a vacuum and only cleaned using a carefully defined procedure to avoid either adding or sloughing off atoms and changing the mass of the reference. (As the unit of kilogram was defined by this reference kilogram, any change in its mass would have changed the very definition of what a kilogram was!) However, because a reference item is inherently prone to changing over time, and because it must be so carefully preserved and maintained, it is less useful than a scientific justification of the unit of mass. In 2019, a scientific justification of the unit of kilogram was formulated based on the value of Planck’s constant.

SI derived units

All other units can be derived from base units and are therefore called derived units. For example, the unit used for velocity (meters per second) is derived from the base units of meter and second: m/s.

The joule is a unit of energy and work, and is derived from the base units of kilograms, meters, and seconds: kg.m2/s2. The coulomb is a unit of electrical charge, and is derived from the base units of ampere and second: A.s (second times ampere).

Quantities that are derived from derived units can also have their base units determined. For example, a volt is defined as a joule divided by a coulomb. Because we know the base units of joule and coulomb, we can derive the base units of a volt:

    \begin{align*} \textrm{V} &= \frac{\textrm{J}}{\textrm{C}}\\ &= \frac{\frac{\textrm{kgm}^2}{\textrm{s}^2}}{\textrm{sA}}\\ &= \frac{\textrm{kgm}^2}{\textrm{s}^3\textrm{A}}. \end{align*}

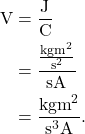
SI prefixes

At times, there are quantities that are either extremely small or extremely large. Instead of using scientific notation to deal with these quantities, we can instead use prefixes. The SI prefixes have been standardized for use with the International System of Units (SI). These prefixes can be used with any type of SI unit: meter, volt, second, gram, and so on. Common SI prefixes that are used in this textbook are defined in the table below.

prefix

symbol

multiplicative factor

example

atto

a

10^{-18}

am (attometers)

femto

f

10^{-15}

fm (femtometers)

pico

p

10^{-12}

pm (picometers)

nano

n

10^{-9}

nm (nanometers)

micro

\mu

10^{-6}

\mum (micrometers)

milli

m

10^{-3}

mm (millimeters)

10^0

m (meters)

kilo

k

10^3

km (kilometers)

mega

M

10^6

Mm (megameters)

giga

G

10^9

Gm (gigameters)

tera

T

10^{12}

Tm (terameters)

peta

P

10^{15}

Pm (petameters)

exa

E

10^{18}

Em (exameters)

How to convert units

When performing numerical calculations in physics, we frequently need to convert a quantity from one type of unit to another (for example, we may need to convert from cm to m).

To perform a conversion, we rely on the algebraic rule that any value can be multiplied by one without changing its value. If the conversion between units is known, the ratio of one unit to the other will be equal to one. The following examples will demonstrate this.

To convert 3.65 m (meters) to cm (centimeters), the conversion factor between m and cm must be known. There are 100 cm in 1 m. Because we want to convert m to cm, we need to multiply 3.65 m by the ratio containing the unit cm in the numerator and the unit m in the denominator:

    $$(3.65~\textrm{m})\left(\frac{100~\textrm{cm}}{1~\textrm{m}}\right).$$

The units of m will cancel out in this equation, resulting in a final unit of cm. The result is

    $$(3.65)(100~\textrm{cm}) = 365~\textrm{cm}.$$

Unit conversions may require more than one conversion factor. Consider the specific heat capacity of water, which is 1 cal/(gCo). To determine the specific heat capacity with units of J/(kgK), we must convert between cal (calories) and J (joules), between g (grams) and kg (kilograms), and between Co (Celsius degree) and K (kelvin). To do this, we can simply multiply by all three ratios, ensuring that the ratios are configured so that units of cal, g, and Co will cancel out. This will yield

    $$\left(1~\frac{\textrm{cal}}{\textrm{gC}^{\circ}}\right)\left(\frac{4.184~\textrm{J}}{1~\textrm{cal}}\right)\left(\frac{1000~\textrm{g}}{1~\textrm{kg}}\right)\left(\frac{1~\textrm{C}^\circ}{1~\textrm{K}}\right).$$

The result will be

    $$(1)(4.184~\textrm{J})\left(\frac{1000}{\textrm{kg}}\right)\left(\frac{1}{\textrm{K}}\right) = 4184~\frac{\textrm{J}}{\textrm{kgK}}.$$

If a unit is raised to a power (squared or cubed, for example), then a conversion can be raised to the same power. For example, to convert the density of water (which is 1 g/cm3) into units of kg/m3, convert g to kg, and then cube the conversion between cm and m:

    $$\left(1~\frac{\textrm{g}}{\textrm{cm}^3}\right)\left(\frac{1~\textrm{kg}}{1000~\textrm{g}}\right)\left(\frac{100~\textrm{cm}}{1~\textrm{m}}\right)^3 = \left(1~\frac{\textrm{g}}{\textrm{cm}^3}\right)\left(\frac{1~\textrm{kg}}{1000~\textrm{g}}\right)\left(\frac{1000000~\textrm{cm}^3}{1~\textrm{m}^3}\right).$$

The result is

    $$(1)\left(\frac{1~\textrm{kg}}{1000}\right)\left(\frac{1000000}{\textrm{m}^3}\right) = 1000~\frac{\textrm{kg}}{\textrm{m}^3}.$$

Common unit conversions

Length

1 inch = 2.54 cm

1 foot = 0.3048 m

1 m = 39.37 in

1 mi = 1.609 km

Volume

1 L = 10-3 m3

Time

1 year = 365.25 days

1 day = 24 hours

1 hour = 60 minutes

1 minute = 60 seconds

Mass

1 kg = 1000 g

1 kg has a weight of 2.205 lb on Earth

Force

1 lb = 4.448 N

Pressure

1 Pa = 1 N/m2

1 atm = 1.01 x 105 Pa

1 lb/in2 (psi) = 6895 Pa

Energy and power

1 cal = 4.184 J

1 kWhr = 3.6 x 106 J

1 eV = 1.6 x 10-19 J

1 hp = 746 W

Temperature

1 Co (change of one degree C) = 1.8 Fo (change of 1.8 degrees F)

1 Fo (change of one degree F) = 5/9 Co (change of 5/9 degree C)

Speed

1 m/s = 3.60 km/hr (kph) = 2.24 mi/hr (mph)

1 km/hr (kph) = 0.621 mi/hr

Physical constants

speed of light in vacuum

3.00 \times 10^{8}~\textrm{m/s}

speed of sound at 20 oC

343~\textrm{m/s}

acceleration due to gravity

9.81~\textrm{m/s}^2

average distance between the Earth and Sun

1.50 \times 10^{11}~\textrm{m}

average distance between the Earth and Moon

3.84 \times 10^8~\textrm{m}

average radius of the Earth

6.37 \times 10^6~\textrm{m}

solar radius

6.96 \times 10^8~\textrm{m}

average radius of the Moon

1.74 \times 10^6~\textrm{m}

mass of the Earth

5.97 \times 10^{24}~\textrm{kg}

mass of the Sun

1.99 \times 10^{30}~\textrm{kg}

mass of the Moon

7.34 \times 10^{22}~\textrm{kg}

mass of a proton

1.67 \times 10^{-27}~\textrm{kg}

mass of a neutron

1.68 \times 10^{-27}~\textrm{kg}

mass of an electron

9.11 \times 10^{-31}~\textrm{kg}

charge of a proton

+1.60 \times 10^{-19}~\textrm{C}

charge of an electron

-1.60 \times 10^{-19}~\textrm{C}

universal gravitational constant

6.67 \times 10^{-11}~\textrm{Nm}^2\textrm{/kg}^2

Coulomb’s constant

8.99 \times 10^9~\textrm{Nm}^2\textrm{/C}^2

Planck’s constant

6.63 \times 10^{-34}~\textrm{Js}

Avogadro’s number

6.02 \times 10^{23}~\textrm{mol}^{-1}

Further reading

  • SI Units – This website from NIST gives an overview of the international system of units (SI).

Practice questions

Conceptual comprehension

  1. Is it possible to add a distance in feet to a distance in miles? If so, how? If not, why not?
  2. Is it possible to add a Celsius temperature to a Fahrenheit temperature? If so, how? If not, why not?
  3. Is it possible to multiply quantities of different units and get a meaningful result? If so, give an example. If not, why not?

Numerical analysis

  1. A car travels at a speed of 72 km/hr. Convert this speed to meters per second.
  2. A block has a mass of 500 grams. Express this mass in kilograms.
  3. An object is accelerated at 20 m/s2. Calculate the acceleration in terms of km/hr2.
  4. A length of wire measures 25 centimeters. Convert this length to meters.
definition

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book