A. Vectors and vector arithmetic
A vector is a quantity that requires two or more numbers (with units) to be fully described and that obeys certain rules of combination. For our purposes, it will be sufficient to say that a vector quantity is one that requires both a magnitude (strength) and a direction for a complete description. As we saw in our discussion of forces in this textbook, not only can different strengths of forces be applied to an object, they can be applied in different directions.
A quantity that does not contain direction is said to be a scalar quantity. Mass is a scalar. It has a magnitude but no direction. It wouldn’t make any sense for a box to have a mass of 20 kg down, or up, or left, or right. The box would just have 20 kg of mass.
Vector quantities, in this textbook, will be denoted using an arrow over the symbol. For example: ![]() Other textbooks may use a bold font to denote a vector quantity.
Other textbooks may use a bold font to denote a vector quantity.
Drawing vectors
A vector is denoted graphically by drawing it as an arrow. The length of the arrow tells us about the magnitude of the vector. The positioning of the arrowhead tells us the direction of the vector. For example, you can draw an arrow to demonstrate a vector with a magnitude of 10 units pointing down by a certain length. A vector with a magnitude of 20 units pointing down would be twice as long.
Because a vector can be used to represent any direction in three-dimensional space, it can be tricky to discuss the direction of a vector. In this textbook, we’ll mostly limit the discussion of vectors to two-dimensional space. In two dimensions, a vector can be pointed in any of 360 degrees.
Vector direction
One way that we can discuss the direction of a vector is used for vectors that point completely vertically or completely horizontally. For a vertically directed vector, a plus sign means that a vector points up, and a minus sign means that a vector points down. For a horizontal vector, a plus sign means that a vector points to the right, and a minus sign means that a vector points to the left. This is the same as the signs used in the Cartesian coordinate system.
Alternatively, we could use a cardinal direction such as north, south, east, or west to define the direction of a vector. This is not always relevant, but can be a nice way to talk about direction when discussing changes in location, for example.
Finally, we could use angle relative to a reference direction to discuss direction. It is customary to use the positive x-axis as the reference direction. This is how direction is used for vectors in many physics classes. Although we will discuss angles at times, we will not be making use of trigonometry in this textbook.
|
Cartesian direction |
cardinal direction |
angle |
|
up |
north |
90 degrees |
|
down |
south |
270 degrees |
|
left |
west |
180 degrees |
|
right |
east |
0 degrees |
Vector components and magnitude
Any vector, regardless of its direction, can be broken down into components. Those components can be used to calculate the magnitude (length) of the vector. The magnitude of a vector will always be a positive number (length cannot be negative).
The Pythagorean theorem states that
![]()
where ![]() and
and ![]() are the lengths of two sides of a right triangle, and
are the lengths of two sides of a right triangle, and ![]() is the hypotenuse of that triangle, as shown in Figure A.1.
is the hypotenuse of that triangle, as shown in Figure A.1.
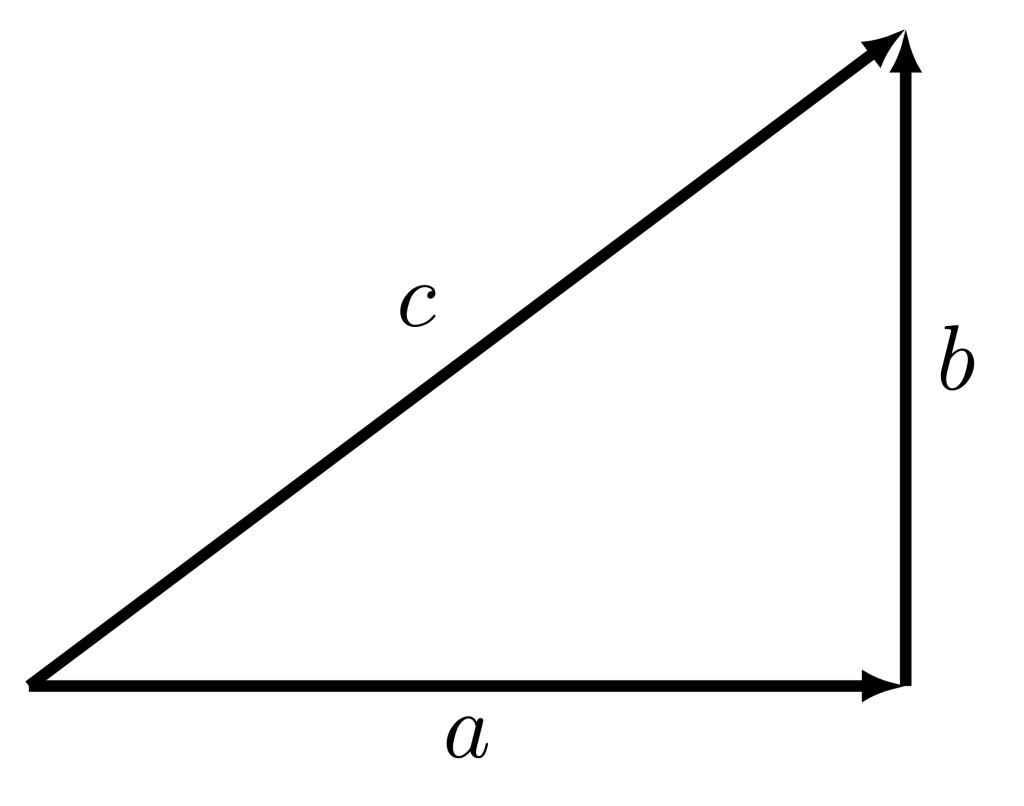
By splitting a vector into horizontal and vertical components, we have found that right triangle. Once both the horizontal and vertical coordinates of a vector are known, the Pythagorean theorem is used to calculate the magnitude of the vector, using the equation
![]()
where ![]() is the horizontal component of the vector,
is the horizontal component of the vector, ![]() is the vertical component of the vector, and
is the vertical component of the vector, and ![]() is the magnitude of the vector.
is the magnitude of the vector.
On the other hand, if the magnitude and direction of a vector are known, the horizontal and vertical components can be found graphically by projecting the shadow of the vector on the x-axis and y-axis, respectively (as shown in Figure A.2). To do this mathematically generally requires the use of trigonometry and thus will not be discussed further.
Horizontal vector
The vector shown in Figure A.3 has a starting position of (4,0) and an ending position of (0,0). The arrow will point from the start to the end. This is a horizontal line pointing toward the left. Because the vector is purely horizontal, there is no vertical component associated with it.
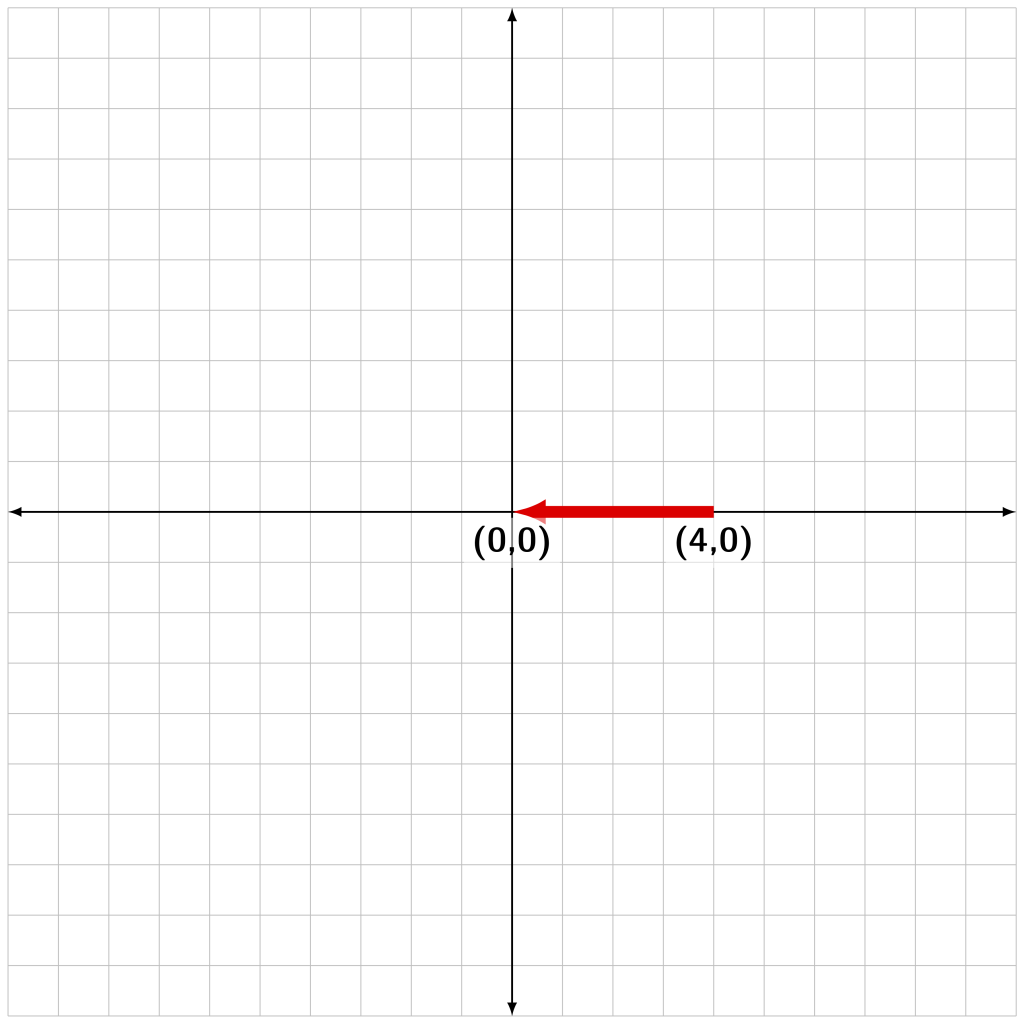
The horizontal component of the vector is equal to the final x position of the vector minus the initial x position of the vector:
![]()
The vector in Figure A.3 has an x component of
![]()
The negative sign of the component indicates that the direction of the vector points to the left (which is defined as negative using the Cartesian coordinate system). The magnitude (length) of the vector is four.
Vertical vector
The vector shown in Figure A.4 has a starting position of (-3,-2) and an ending position of (-3,5). The arrow points from start to finish. This is a vertical line pointing upward. This vector is completely vertical and has no horizontal component to it.
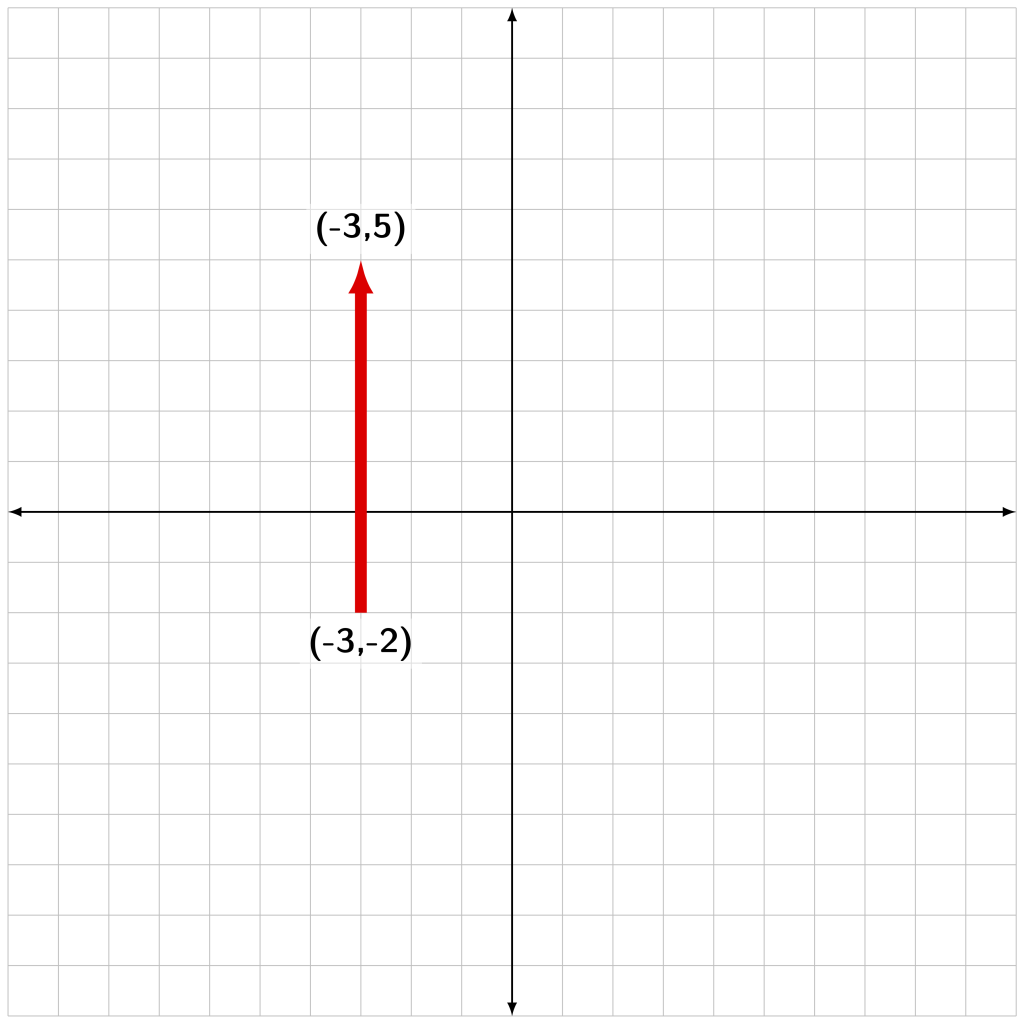
The vertical component of the vector is equal to the final y position of the vector minus the initial y position of the vector
![]()
The vector in Figure A.4 has a y component of
![]()
The y component of the vector is therefore equal to positive seven. The positive sign indicates that it points up. The magnitude of the vector is seven, which describes the vector’s length.
Two-dimensional vector
The next example, shown in Figure A.5, has a starting location of (-4,-1) and an ending location of (6,8). The arrow points from start to finish. This vector has both horizontal and vertical components.
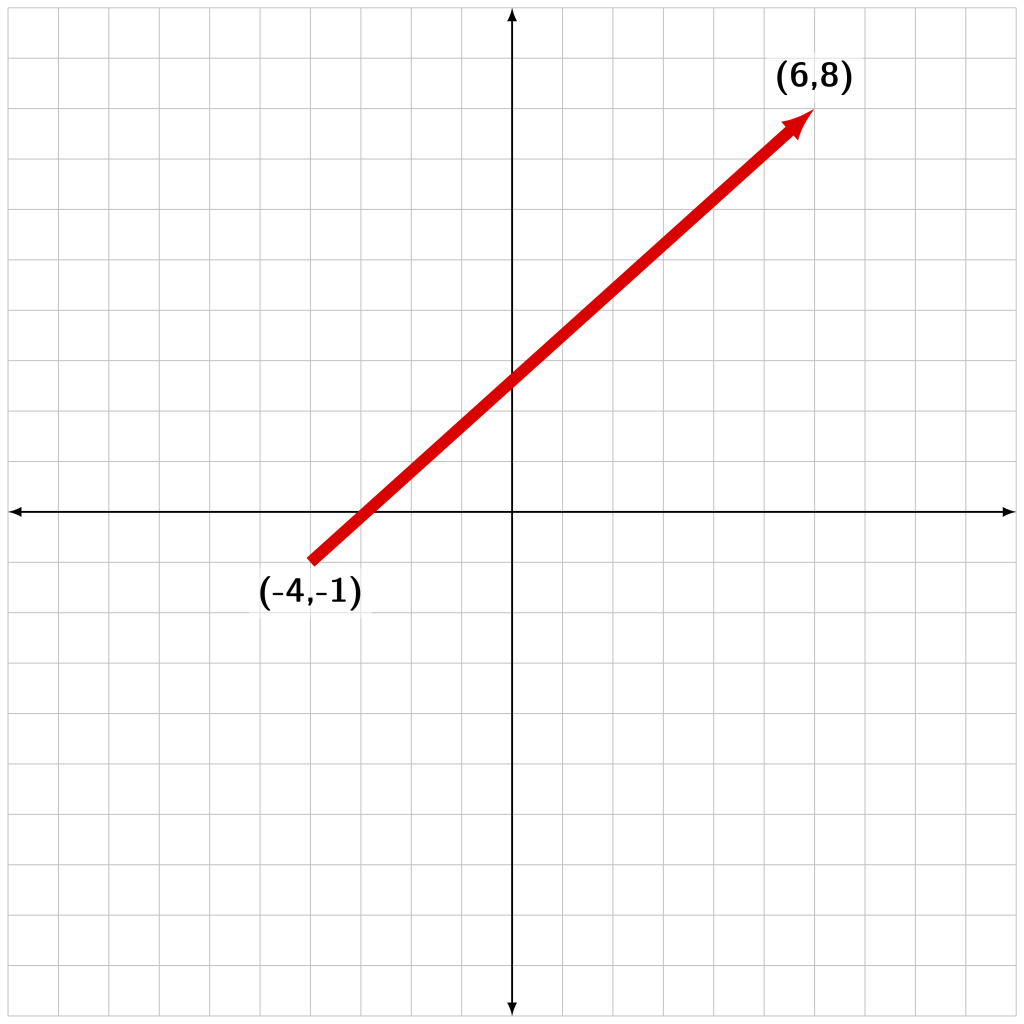
The horizontal component defines the horizontal motion of this vector, ignoring the vertical parts. The horizontal component is
![]()
The vertical component defines the vertical motion of the vector, ignoring the horizontal parts. The vertical component is
![]()
Now that we know the value of each component, we can use the Pythagorean theorem to calculate the magnitude of the vector itself. In this example, the magnitude is
![]()
Adding vectors
What if we want to add two or more vectors together? Sometimes we will need to do this, especially when calculating the sum of all forces acting on an object to determine whether or not it is in equilibrium. There are two methods for adding vectors together: the graphical method and the algebraic method. Either one can be used. Both will give the same result. Try both of them and use the one that feels more comfortable to you.
Graphical method
To add vectors graphically, draw one of the vectors (typically starting at the origin). Then, at the tip of that vector, draw the second vector. If there are more than two vectors, each will be connected together tail to tip, tail to tip. The order in which you draw the vectors does not matter. The sum of the vectors is the straight line from the start of the first vector to the end of the last vector.
Consider two vectors with components of (4,9) and (-6,-5). Each individual vector is drawn tail to tip, and the overall sum vector is drawn from the origin to the end of the last vector. This is represented in Figure A.6.
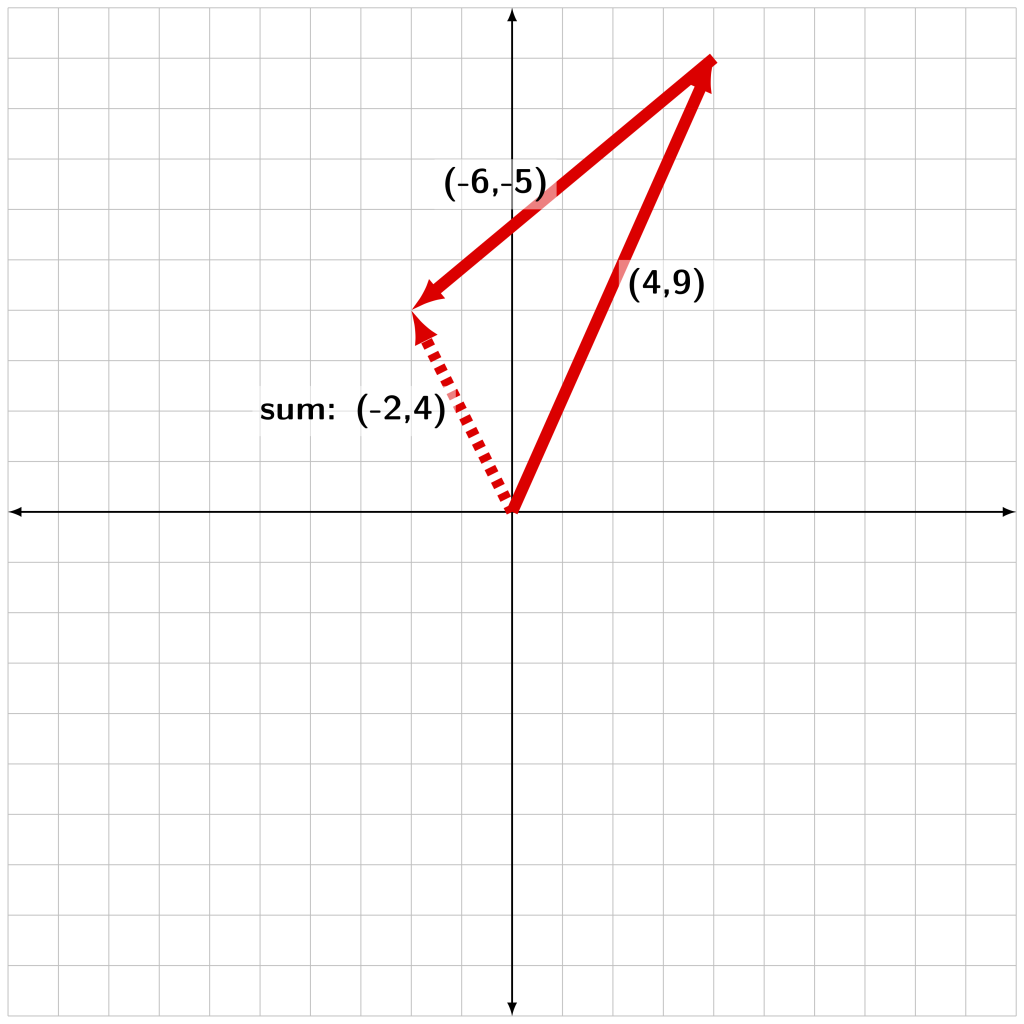
In this example, the sum vector has a horizontal component of negative two and a vertical component of positive four: (-2, 4). The Pythagorean theorem can be used to calculate the magnitude of the sum of the vectors:
![]()
Algebraic method
Alternatively, we can add the two vectors together algebraically. To add the vectors algebraically, write out each vector as a set of components. The first vector is (4,9), and the second vector is (-6,-5). Add all of the x components together.
![]()
Then add all of the y components together.
![]()
Therefore, the sum of the vectors is (-2, 4). Note that we should, and did, get the same result using both methods (graphical and algebraic). If there are more than two vectors, simply add all of the x components together to find the x component of the sum. Then add all of the y components together to find the y component of the sum.
Vector properties
There are certain important properties that apply when doing arithmetic with vector quantities.
Commutativity of addition
When adding vectors, addition is a commutative property. That is,
![]()
The order in which we add vectors does not matter! Consider two vectors, ![]() and
and ![]() . Figure A.7 demonstrates the addition of
. Figure A.7 demonstrates the addition of ![]() which has a sum of (-7,3).
which has a sum of (-7,3).
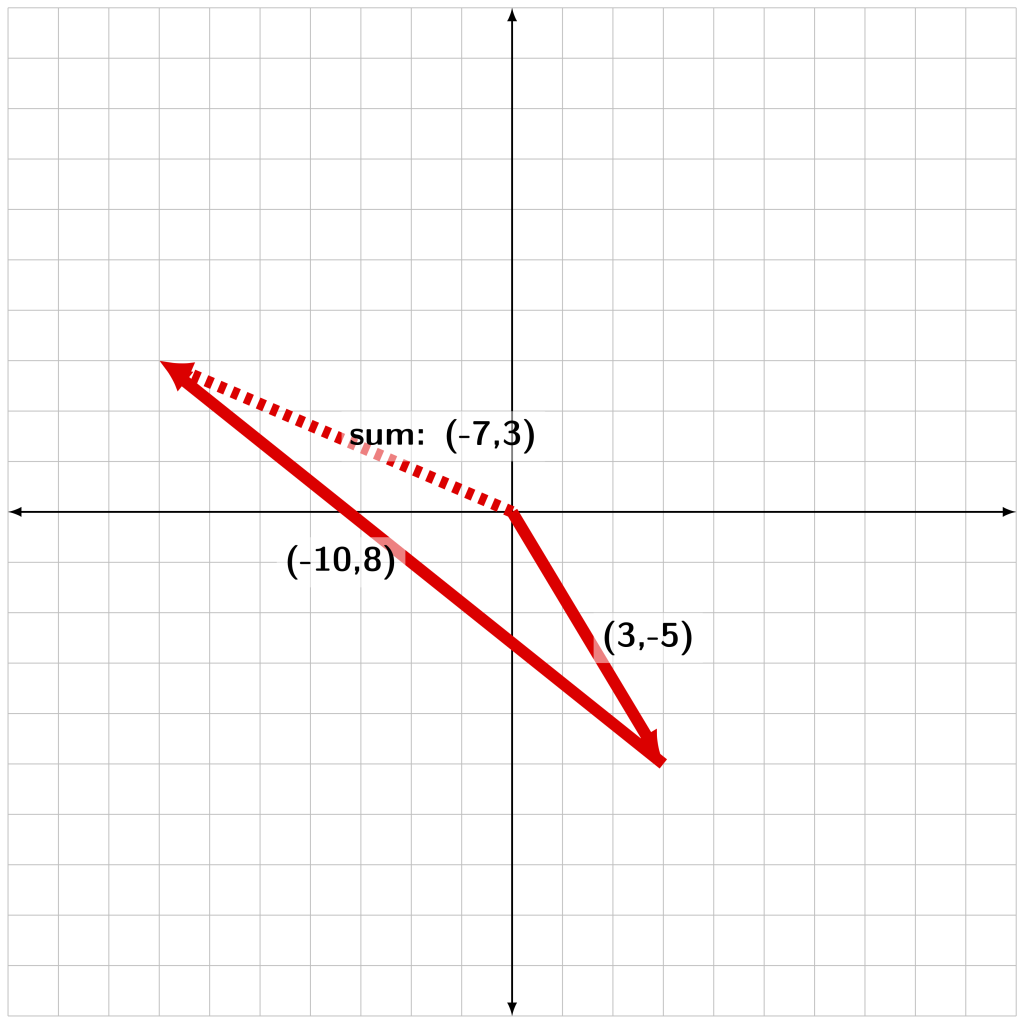
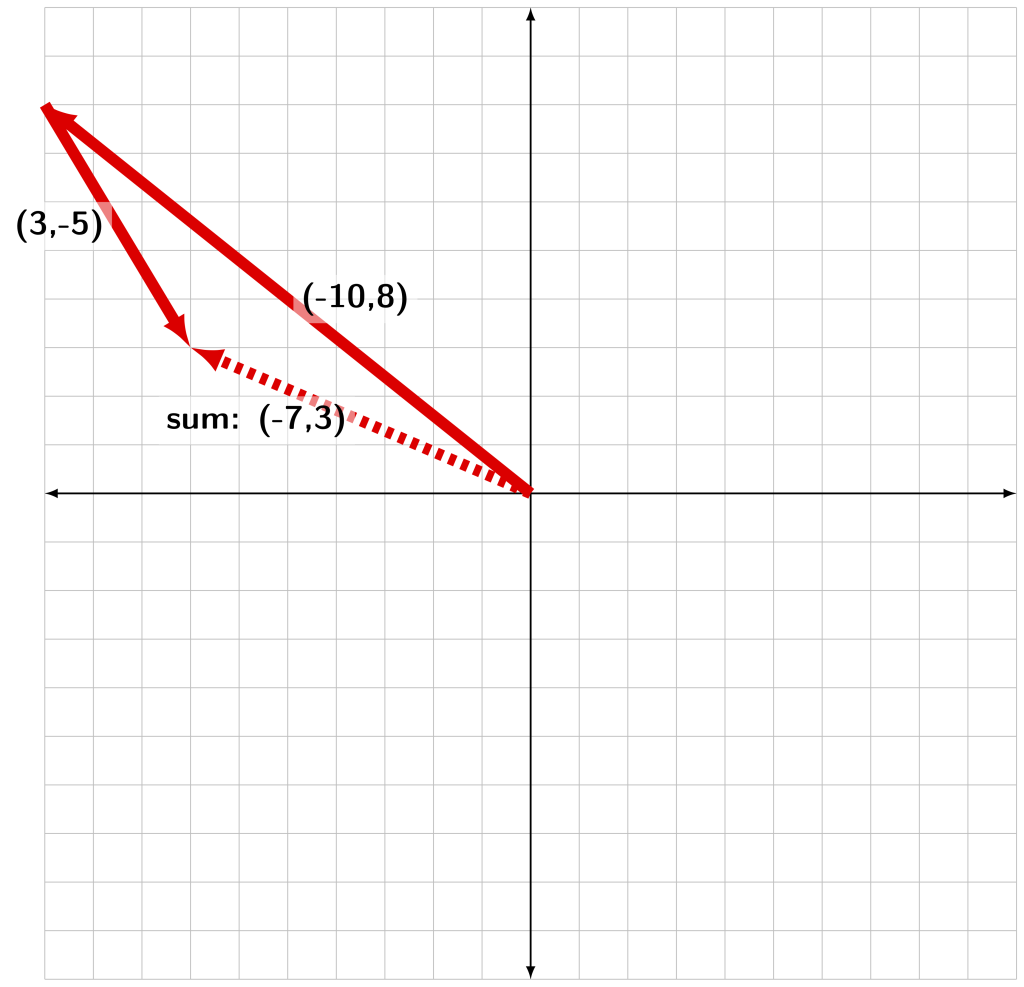
Figure A.8 demonstrates the addition of ![]() which also has a sum of (-7,3). This shows that the order of addition does not matter. This is not only true for two vectors: when adding any number of vectors together, the order does not matter!
which also has a sum of (-7,3). This shows that the order of addition does not matter. This is not only true for two vectors: when adding any number of vectors together, the order does not matter!
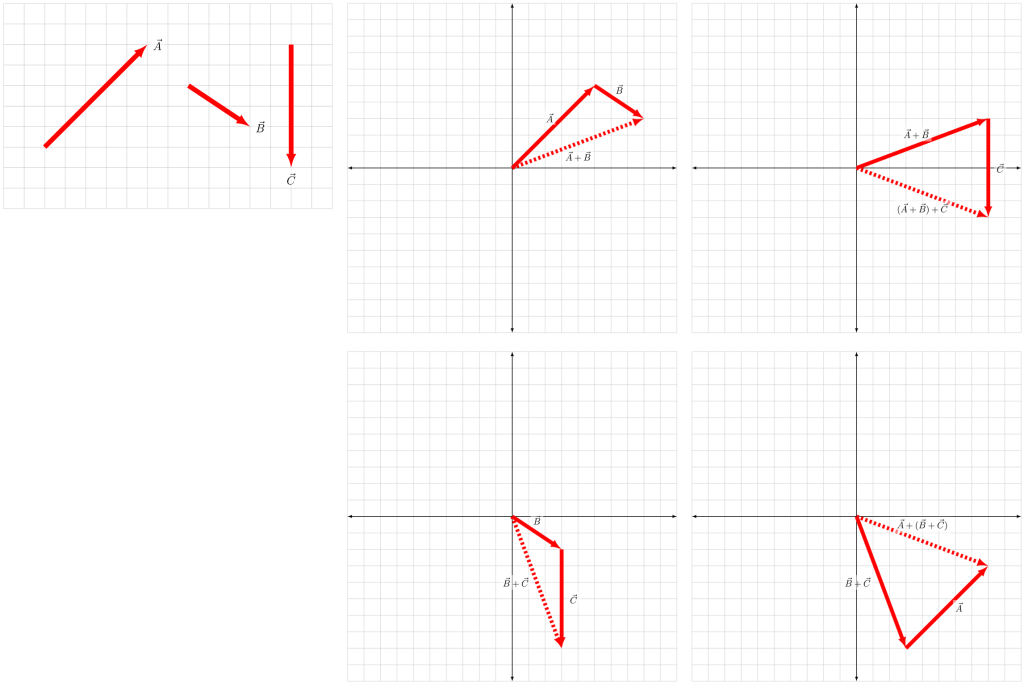
Associativity of addition
Vectors obey the associative property for addition. That is,
![]()
This property is demonstrated in Figure A.9, where vectors ![]() (5,5),
(5,5), ![]() (3,-2), and
(3,-2), and ![]() (0,-6) are added in both orders with the same result (8,-3).
(0,-6) are added in both orders with the same result (8,-3).
Scalar multiplication
It is possible to multiply a vector by a scalar. That is,
![]()
Consider the example of ![]() . When multiplied by (for example) positive two, the result is
. When multiplied by (for example) positive two, the result is ![]() . It is also possible to multiply the vector by (for example) negative one half. That result is
. It is also possible to multiply the vector by (for example) negative one half. That result is ![]() . These results are demonstrated graphically in Figure A.10.
. These results are demonstrated graphically in Figure A.10.
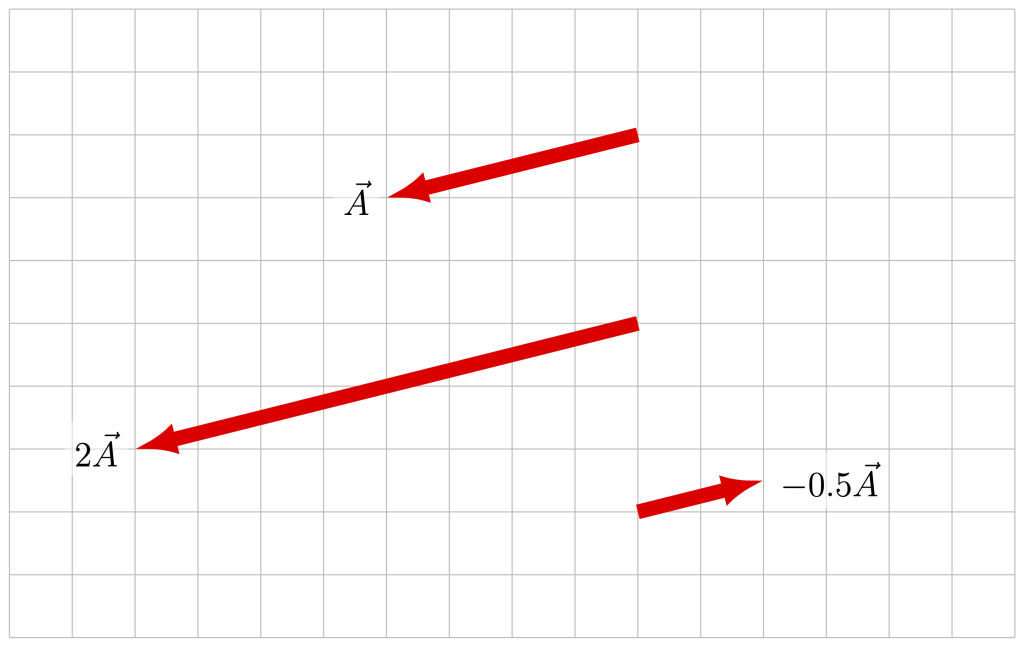
Because it is possible to multiply a vector by a negative scalar value, we can think of subtraction as addition performed after scalar multiplication. In other words,
![]()
Further reading
- PhET vector addition simulation – Use this simulation to practice adding vectors together.
- Vector addition: does order matter – Play with this simulation to see for yourself that the order in which you add vectors does not matter.
Practice questions
Conceptual comprehension
- Recall that a vector quantity is one in which two or more numbers with units are needed for a complete description. For example, a complete description of a location on a two-dimensional grid can be provided by the x-component and the y-component of the vector. What are two different numbers that could be used to completely describe the same vector?
Numerical analysis
- Vector
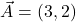 . Calculate the magnitude of this vector.
. Calculate the magnitude of this vector. - Vector
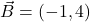 . Calculate the magnitude of this vector.
. Calculate the magnitude of this vector. - Vector
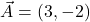 , and vector
, and vector 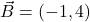 . Calculate the components of the resultant vector
. Calculate the components of the resultant vector 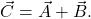 Then, calculate the magnitude of the resultant vector
Then, calculate the magnitude of the resultant vector 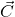 .
. - Vector
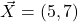 . Calculate the magnitude of this vector.
. Calculate the magnitude of this vector. - Vector
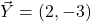 . Calculate the magnitude of this vector.
. Calculate the magnitude of this vector. - Vector
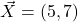 , and vector
, and vector 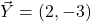 . Calculate the components of vector
. Calculate the components of vector 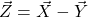 . Then, calculate the magnitude of vector
. Then, calculate the magnitude of vector  .
.
Hands-on experiments
- If you have access to safe outdoor space, walk, run, or roll to a particular spot (feel free to mark it with an object) that you will call the origin. Then move 5-10 meters (the exact distance does not matter as long as you try to be consistent) east (or west), followed by moving 5-10 meters north (or south). Consider your new location with respect to the origin. What is your displacement? If you start by moving north/south, and then east/west, does that affect your displacement?
- If you regularly commute to work, school, or another common location, look at a map and consider all of the different routes you can take between your starting and ending locations. Which has the shortest path? Which has the longest path? Does the choice of path affect the displacement? Along your commute, consider your instantaneous speed and velocity. After your commute, consider your average speed and velocity.
A vector quantity is a variable that must be conveyed with both a numerical quantity (indicating magnitude or strength) and a direction.
A force is a push or a pull that causes an object to change its motion. More fundamentally, force is an interaction between two objects. (symbol: F, unit: N)
A scalar quantity is a variable that can be conveyed with a numerical quantity indicating magnitude or strength.
Absorption of light occurs when light waves completely transfer their energy to a medium as they attempt to pass through it. The light is therefore blocked from transmitting through the medium.
Physics is a branch of science that focuses on the fundamentals of the workings of our universe.
Displacement describes the straight-line distance from one point to another. Displacement is a vector quantity. (symbols: Δd [for general displacement], Δx [for horizontal displacement], Δy [for vertical displacement]. unit: m).

