8. Rotational motion

Summary

Rotational motion is all about things that rotate. So far, our discussion has been focused on translational motion: motion along a straight line. But translational motion can’t help us fully understand the motion of things like bicycle wheels, bowling balls, figure skaters, propellers, or even the motion of stars and planets. We need new concepts to help us understand rotational motion.

Rotational speed

Rotational speed quantifies how quickly (or slowly) something rotates about an axis. The symbol for rotational speed is the lowercase Greek letter omega (\omega). There are many different units that we could use for rotational speed, depending on how we want to measure a rotation, including

  • revolutions (or rotations) per unit of time (e.g., RPM, rev/s),
  • degrees per unit of time (e.g., degrees per second), and
  • radians per unit of time (e.g., rad/s).

One revolution consists of 360 degrees or 2\pi radians. These are the ratios used to convert between the different types of rotational speed units.

All objects on the same rotating platform will experience identical rotational speeds. For example, on a playground merry-go-round (as seen in Figure 8.1), all of the people sitting on the merry-go-round as it spins will be traveling at exactly the same rotational speed. They will all move 360 degrees (or 2\pi radians) as the disk makes a single rotation in the same interval of time.

A small child sits on a playground merry-go-round. Because of the spinning of the merry-go-round, the background is blurry.
Figure 8.1 – A child sits on a merry-go-round as it spins. All objects on the spinning disk are rotating with the same rotational velocity. Playing on the Merry go round, by Charles Knowles, is licensed under CC BY 2.0.

A geostationary satellite orbits the Earth at a distance such that it appears not to move with respect to objects on the ground. An observer standing directly underneath the satellite would not be able to see any motion of that satellite.

We can calculate the rotational speed of a geostationary satellite, knowing that it makes a complete orbit of the Earth every 24 hours. First, convert 24 hr to units of minutes and seconds

    \begin{align*} 24~\textrm{hr} = (24~\textrm{hr})(\frac{60~\textrm{min}}{1~\textrm{hr}}) &= 1440~\textrm{min}\\ = (1440~\textrm{min})(\frac{60~\textrm{s}}{1~\textrm{min}}) &= 86400~\textrm{s}. \end{align*}

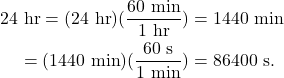
Using units of revolutions per minute (RPM), one revolution of the satellite occurs every 1440 min, giving a rotational speed of

    \begin{align*} \omega &= \frac{1~\textrm{rev}}{1440~\textrm{min}}\\ &= 6.94 \times 10^{-4}~\textrm{RPM}. \end{align*}

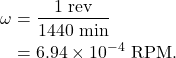
We can convert this rotational speed to use units of degrees per second

    \begin{align*} \omega &= (6.94 \times 10^{-4}~\textrm{RPM})(\frac{360^\circ}{\textrm{rev}})(\frac{1~\textrm{min}}{60~\textrm{s}})\\ &= 0.004~^\circ/\textrm{s}. \end{align*}

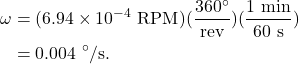
Converting to rotational speed with units of radians per second, we find that

    \begin{align*} \omega &= (6.94 \times 10^{-4}~\textrm{RPM})(\frac{2\pi~\textrm{rad}}{\textrm{rev}})(\frac{1~\textrm{min}}{60~\textrm{s}})\\ &= 7.27 \times 10^{-5}~\textrm{rad/s}. \end{align*}

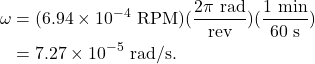
Tangential velocity

Have you ever ridden on a merry-go-round or a carousel? The way we experience speed on a rotating platform has to do not only with the rotational speed of the ride, but also with how far we are from the center of rotation. This quantity is called tangential velocity. While rotational speed is constant everywhere along a rotating object, the tangential velocity is not.

Tangential velocity is very similar to the velocity that was defined earlier in this textbook. It is the linear distance that something travels as it rotates per unit of time. Instead of quantifying the rotation in terms of revolutions, degrees, or radians, the actual distance traveled (with units of meters) is used. The symbol is a lowercase v with a subscript of t to make it clear that it’s a tangential velocity (v_t). The unit is m/s.

The direction of the tangential velocity is tangent to the motion of the rotation: hence the name tangential velocity. As an object rotates, the tangential velocity will continue to rotate in order to point tangent to the direction of the rotational motion. Consider using a sling to rotate an object around in circles before letting it go. The tangent is the direction the object will go when it is released and stops rotating.

To calculate tangential velocity, determine the physical distance that an object moves as it travels along the spinning object per unit of time.

The distance around a circle is known as the circumference. It is equal to

    $$C = 2\pi r,$$

where r is the radius of the circle. Therefore, the magnitude of the tangential velocity will be equal to

    $$v_t = \frac{2\pi r}{t},$$

where r is the distance (in meters) that the object is from the center of rotation and t is the time (in seconds) to complete one full rotation. Note that 2 times \pi divided by time is equal to the rotational speed of an object in units of rad/s. Therefore if the rotational speed is known with units of rad/s, tangential velocity can be calculated using the equation

    $$v_t = \omega r.$$

The closer an object is to the center of rotation, the smaller the tangential speed. The farther away it is from the center of rotation, the higher the tangential speed. The reason that we feel like we’re moving faster when we sit in the outer part of a carousel or merry-go-round is because our tangential velocity is higher.

The altitude of a satellite in geostationary orbit is 36 million meters, and the radius of the Earth is 6.4 million meters. Therefore, a geostationary satellite is 42.4 million meters away from the center of rotation. The time of one rotation, as discussed above, is 86400 s. The tangential velocity of a geostationary satellite is therefore

    \begin{align*} v_{t} &= \frac{2\pi(42400000~\textrm{m})}{86400~\textrm{s}}\\ &= 3083~\textrm{m/s}. \end{align*}

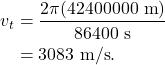
Rotational acceleration

Acceleration, as we have seen earlier in this textbook, means one of three things: speeding up, slowing down, or changing direction. It’s possible for the rotational speed of an object to change. Rotational acceleration therefore quantifies how rapidly the rotational speed of an object changes (speeds up, slows down, or changes direction). We will not quantify rotational acceleration in this textbook; it is only being mentioned to give you a more complete understanding of rotational motion.

Newton’s second law states that force generates changes in linear motion (which are resisted by inertia). In order to generate changes in rotational motion, a new quantity called torque is introduced. Below, we’ll see that torque generates such changes. Furthermore, just as mass resists changes in linear acceleration, a quantity called rotational inertia resists changes in rotational motion.

Rotational inertia

Rotational inertia is a measure of how much an object resists changes to its rotational speed. If an object is not rotating, rotational inertia is related to how difficult it is to get that object to start rotating. If it’s already rotating, rotational inertia is related to how hard it is to make that rotation speed up or slow down.

Rotational inertia comes from two things: the mass of an object and how that mass is distributed with relation to the center of rotation of the object. The more massive an object is, the harder it is to get it to start rotating. The distribution of that mass is important as well. The farther away the mass is distributed from the object’s center, the harder it is to get it to start rotating.

In the video below, there are two objects that are very similar to each other: a hoop and a disk. The hoop is hollow on the inside, and the disk is solid. But they have the same radius and both have a mass of 0.5 kg (see Figure 8.2).

On the left, a solid wooden disk is photographed on a balance with a readout of 505.5 g. On the right, a metallic hoop is photographed on a balance with a readout of 508.5 g.
Figure 8.2 – A solid wooden disk has a mass of 505.5 g (0.5 kg), left. A metallic hoop has a mass of 508.5 g (0.5 kg), right. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Both objects have the same mass and therefore the same translational inertia (in other words, it would take the same amount of effort to shake either object back and forth). Because the disk is solid, its mass is uniformly distributed throughout. The hoop, however, has its mass concentrated at the edges of the circle, far from the center of the hoop. This means that the hoop will have more rotational inertia than the solid disk. Therefore, we can predict that the hoop will take longer to roll down the track than the solid disk. We can see that this is the case by watching the video below.

It is possible to quantify rotational inertia using equations depending on the shape and distribution of mass of an object. However, the mathematics behind rotational inertia is beyond the scope of this textbook, so it will not be covered.

Torque

Torque is a twist or a turn that causes an object to change its rotational motion. Just as force creates acceleration and makes something moving in a straight line speed up, slow down, or change direction, torque creates rotational acceleration and causes the rotation to speed up, slow down, or change direction. Torque has a symbol of the lowercase Greek letter tau (\tau). The unit of torque is called the newton-meter (Nm). Because torque is so different from concepts such as work and energy, we do not simplify this as joules, but just use newton-meters (Nm), even though they share common units.

Torque is equal to the perpendicular force times the distance between the applied force and the center of rotation, or

    $$\tau = F_{\perp}r.$$

The concept of perpendicular force is important, as not all directions of force contribute to making an object rotate.

Consider using a wrench to tighten a bolt in a piece of furniture. Simply pushing or pulling along the handle of the wrench will not cause the wrench to rotate. It is necessary to push or pull perpendicular to the handle. Figure 8.3 shows three scenarios. In scenario (a), the applied force is completely parallel to the center of rotation. This applied force will not cause any rotation of the wrench, and therefore the torque will be zero. In scenario (b), the applied force is neither all parallel or all perpendicular, but can be broken into parallel and perpendicular components. Only the perpendicular component is applying torque to the wrench, and only that force component will cause the wrench to rotate. In scenario (c), the applied force is all perpendicular. The entirety of the applied force is contributing to the torque. In all three scenarios, the dashed line indicates the distance between the applied force and the center of rotation.

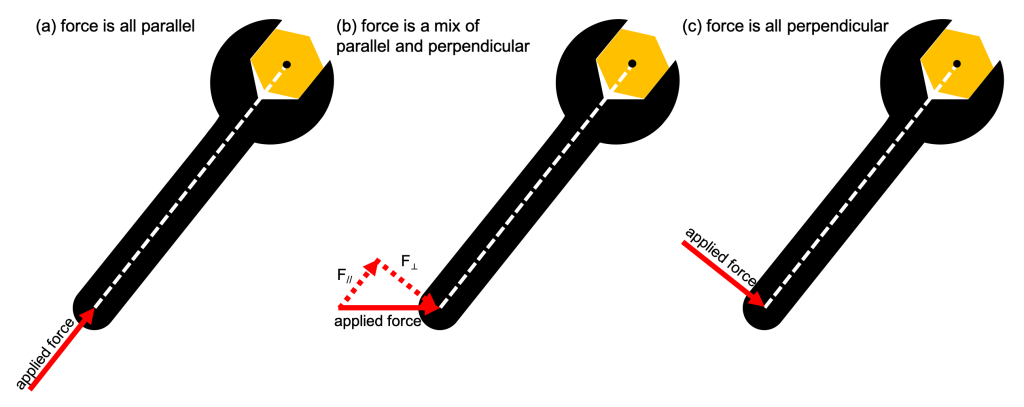
Figure 8.3, described in the text.
Figure 8.3 – A force is applied to a wrench to cause a rotation. (a) The applied force is parallel to the center of rotation. (b) The applied force is neither parallel nor perpendicular to the center of rotation, and can be split into components. (c) The applied force is perpendicular to the center of rotation. The dashed line indicates the distance between the applied force and the center of rotation. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

If you’re familiar with the term “lever arm,” it has to do with that distance between the force and the center of rotation. The longer the lever arm, the easier it is to rotate something. This is why there are extensions that we can put on a socket wrench. If something is really tight, we need to apply a lot of torque to loosen a bolt (for example). There’s only so much force we can apply, so we can use the r in the torque equation to make up for our relative lack of strength.

Mechanical equilibrium

Previously in this textbook, we learned that mechanical equilibrium occurs when an object is traveling at a constant velocity and occurs when the net force on an object is equal to zero. We now have to expand this definition.

Mechanical equilibrium occurs when an object is traveling at a constant velocity and at a constant rotational speed. This occurs when the net force on an object is equal to zero and the net torque on an object is equal to zero.

We learned that forces are positive when they go up or to the right, and negative when they go down or to the left. How do we give sign to torque? We do that by looking at the direction that it would make an object rotate. By common convention, if an object would rotate counterclockwise, we call that a positive torque. A clockwise rotation is generated by a negative torque.

Center of mass

Center of mass is another important concept in rotational motion. The center of mass is the point in an object around which it rotates freely. And if you could somehow pick an object up at that exact point, it would balance perfectly.

Another way to define center of mass is this: the center of mass in an object is the point where, on average, the mass is distributed. In an object that has a uniform shape and density, the center of mass will be in the center of the object.

A meter stick made of wood has a relatively uniform density. In Figure 8.4, Dr. Pasquale balances a meter stick. The center of mass is located at (approximately) the center of the meter stick.

A photograph of Dr. Pasquale, a white lady with brown hair and glasses. She is balancing a meter stick using one finger located under the center of the meter stick. An arrow over this point is labeled "center of mass." In the background is a gray curtain.
Figure 8.4 – Dr. Pasquale balances a meter stick by holding it with one finger directly under its center of mass, which is located at the center of the stick. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

In an object like a hammer, which is made of different materials, the center of mass is no longer in the center of the object. It’s closer to where most of the mass of the object is concentrated. In this case, it will be closer to the head of the hammer. In Figure 8.5, Dr. Pasquale balances a hammer using a single finger. Note the position of the center of mass is much closer to the head of the hammer than the handle.

A photograph of Dr. Pasquale, a white lady with brown hair and glasses. She is balancing a hammer using one finger located near to the head of the hammer. An arrow over this point is labeled "center of mass." In the background is a gray curtain.
Figure 8.5 – Dr. Pasquale balances a hammer by holding it with one finger directly under its center of mass, which is located closer to the metal end of the hammer. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

It’s possible for an object to have a center of mass located where there is no actual mass. For example, a donut (assuming it has uniform density) will have the center of mass located in the center (see Figure 8.6), even though no actual mass is located in that spot.

A photograph of a person's hand holding up a donut with chocolate frosting.
Figure 8.6 – A donut of uniform density will have a center of mass in the center: where no actual mass exists. Woman holding chocolate donut closeup, by Nenad Stojkovic , is licensed under CC BY 2.0.

The hoop from the rotational inertia video (Figure 8.2) also has a center of mass located in the center, even though no actual mass exists at that spot.

Center of gravity

Maybe you’ve heard the term center of gravity (CG). What’s the difference between that and the center of mass (CM)? The answer is: they’re almost the same thing. Center of mass has to do with how the mass of an object is distributed. Center of gravity has to do with how the weight of an object is distributed.

If the force of gravity is equal at every spot in an object, then CM and CG are equal. That’s true for most objects most of the time. The only time we might see a difference is in really tall objects, like skyscrapers.

As of the time this textbook was written, the Burj Khalifa (Figure 8.7) was the tallest building in the world, standing at an impressive 830 meters tall. Assuming that the Burj Khalifa is a rectangular cuboid of uniform density (which is not true, but we’ll make the assumption for purposes of illustrating this concept), then the center of mass would be 415 meters from top and bottom, in the exact center of the building.

A photograph of the Burj Khalifa, a towering skyscraper. There are several other buildings nearby, much shorter than the Burj Khalifa. There is a cloudless blue sky in the background, and a waterway in the foreground of of the photograph.
Figure 8.7 – The Burj Khalifa is the tallest building in the world (as of the writing of this textbook). Burj Khalifa, by Donaldytong, is licensed under CC BY-SA 3.0.

Because the force of gravity changes with respect to the distance from the center of the Earth, the parts of this building that are closer to the ground experience more gravitational force than the parts of this building that are higher in the air.

In that case, even though the mass is distributed in the center of the building, the weight distribution is going to be slightly closer to the bottom and will not be collocated with the center of mass. By how much? Again, assuming that the Burj Khalifa were a solid rectangle of uniform density (which it is admittedly not), the center of gravity would be only a couple of millimeters below the center of mass. That’s not much of a difference. In practice the Burj Khalifa has much of its mass located closer to the base of the building than the top (see Figure 8.7), which would cause the offset between the center of mass and center of gravity to be even smaller than this idealized calculation.

So for the most part, it’s perfectly valid to say that center of mass and center of gravity are the same thing. But we should understand that there may be exceptions.

Stability

Stability has to do with how easily an object will topple over. More accurately, stability has to do with this: If you take an object that is in equilibrium and disturb it, how will its motion change? Will it return to its state of equilibrium? Or, will the object move away from that state of equilibrium toward another state?

An object will stay put if it has a center of mass over the support base. Furthermore, an object is stable if the support base is wide enough to ensure that any motion that the object might make won’t upset that condition.

In the video below, Dr. Fazzini holds a trapezoid-shaped block. At the center of mass of the block, there is a pointer that uses gravity to point downward. When the block is placed such that the pointer points to a spot over the support base, the block remains stable and stays put. In one configuration, the pointer points to a spot that is not over the support base, and when placed down, the block falls over.

This concept can also be demonstrated with the “leaning tower” in the video below. At first, the tower sits in its leaning configuration without toppling over. Because the composition of the tower is unclear, it’s not entirely certain where the center of mass is. But because the tower is staying put, the center of mass must be situated somewhere over the support base.

When the top piece of the tower is rotated by 180 degrees, it topples over to the left. That means that by rotating the top of the tower, the center of mass of the object was moved so that it was no longer over the support, but to the left of it.

Stability can also be demonstrated with a soda can. When a soda can is placed on a table (in the typical orientation that you would place a soda can), the center of mass is over the base, and it stays nice and steady. After drinking just the right amount of liquid, the center of gravity is moved downward closer to the base of the can. Now there’s a second point on which you can rest the can. Dr. Pasquale demonstrates this in the video below, and you can also see still images of both orientations in Figure 8.8.

A photograph of a soda can sitting on its base on a lab table (left). A photograph of the same soda can resting on the lip between the base and side of the can (right).
Figure 8.8 – A soda can with just the right amount of liquid is stable on its base (left) as well as on the lip between the base and side of the can (right). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

While the soda can is capable of balancing on its base and on the small lip between the base and the side of the can, the latter configuration is not terribly stable. The application of even a very small torque on either the top or sides of the can will cause the soda can to topple over and disturb its equilibrium.

Stability is a very important consideration in aircraft such as airplanes. Pilots have to be careful to distribute the weight of the passengers and baggage in an airplane in such a manner that the airplane remains stable. (This is known as weight and balance.) This is a routine consideration that pilots make in every flight. If you’ve ever flown on an airline and been asked to move your seat more forward in the airplane, or to a seat farther to the back, it’s probably because the pilot needed to adjust the balance of the airplane.

Angular momentum

Momentum is inertia in motion. Angular momentum is rotational inertia in rotational motion. Angular momentum is equal to the rotational inertia multiplied by the rotational speed. While we will not do calculations with that equation in this textbook, you do not need to know the equation to understand the topic.

Just as momentum is conserved in a system where there is no net external force, angular momentum will be conserved as well, as long as there is no external torque acting on a system. That means that as long as there’s nothing to speed up or slow down a rotating object, its angular momentum will stay the same. Not necessarily the rotational speed, but the angular momentum.

In the video below, Dr. Pasquale has gotten herself rotating in a spinning chair while holding some dumbbells. As long as she doesn’t move, and as long as friction doesn’t slow her down too much, her rotational speed will stay the same because her rotational inertia will not change, and because there are no external torques.

As Dr. Pasquale extends her arms out, she increases her rotational inertia. Because momentum is conserved, when her rotational inertia is increased, her speed will have to slow down to compensate, and it does. When she pulls her arms back in, she reduces her rotational inertia. Her speed will increase to compensate for that change, and to keep the angular momentum the same.

This is the same concept that you may have seen if you have watched or participated in figure skating. In a move called a scratch spin, a figure skater will start spinning, then pull their arms in tight and cross their legs to reduce their rotational inertia as much as possible. This has the effect of causing the skater to speed up, sometimes spinning at a very fast rate. At the conclusion of a spin, a figure skater will expand their arms and free leg, causing their rotation to slow down again due to the increase in their rotational inertia.

Centripetal force

Now we’re going to talk not about rotation, but about motion along a circular path. When an object moves along a circular path at a constant speed, its direction is constantly changing. If the direction changes, there must be an acceleration. When there is acceleration, we know that a force must be acting on that object. We call that force centripetal force. The symbol for centripetal force is F with a subscript of C (F_c). The unit for centripetal force is the newton (N). The equation for centripetal force is

    $$F_c = \frac{mv_t^2}{r},$$

where m is the mass of the object, v_t is the magnitude of the tangential velocity of the object, and r is the radius of the circular path. Centripetal force always points toward the center of the circular path.

Centripetal force isn’t a separate force in and of itself, but is a force that must be supplied by some means to keep something moving in that circular path. Some common forms of circular motion, and the source of the centripetal force used to achieve that, are listed in the table below.

circular motion

source of centripetal force

orbiting satellite

gravity

driving in a circular path on a flat road

friction

airplane turning

lift

rotating an object in a sling (see Figure 8.9)

tension

roller coaster loop

support (normal) force and gravity

When you drive a car around a circular path, the centripetal force is supplied by friction between the tires and the pavement. The faster the car is going, the higher that force needs to be. That’s why we usually slow down to turn when we drive. Also, the tighter the turn we want to take, the more force that’s needed. If the roads are slippery, then it’s harder to get enough friction to move in a circular path.

Centrifugal force (not a real force)

It is often difficult for students first learning physics to accept the fact that the force required to make something move in a circle (the centripetal force) is a “center-seeking” force. That is, the force is directed toward the center of the circle. If you have ever ridden a merry-go-round on a playground or have ridden on a spinning ride at an amusement park, you may have noticed that it feels like you are being pulled outward. This “center-fleeing” sensation is called a centrifugal force. However, the centrifugal force is not a real force. Rather, this sensation is merely due to inertia and your perspective.

According to Newton’s first law of motion, a moving object tends to continue moving in a straight line at constant speed unless acted upon by a force. Consider a car driving around a sharp curve. Suppose you are a passenger in the car while it makes a sharp turn to the left. If you chose not to wear your seat belt (not a good idea), you would “feel” like you are being pulled to the right toward the door, which is away from the center of the circular motion. As the car rounds the curve to the left, you, the passenger, want to keep on moving in a straight line. However, you are not being pulled outward. Rather, you are being pushed inward. Here’s why: as the car turns to the left, the passenger door of the car moves into you and pushes you to the left, forcing you to round the curve with the car. You are sensing that you are being pulled outward due to Newton’s third law of motion. The action of the door pushing inward on you (forcing you to turn in a circle) produces the reaction of you pushing against the door, giving you the sensation that you are being pulled outward when you actually are not.

Centripetal acceleration

Newton’s second law states that forces create acceleration. Centripetal force causes an object to change its direction, which is a type of acceleration. We call that centripetal acceleration.

Centripetal force is equal to mass times centripetal acceleration. Using Newton’s second law to calculate the equation for centripetal acceleration, we find that

    \begin{align*} a_c &= \frac{mv_t^2/r}{m}\\ &= \frac{v_t^2}{r} \end{align*}

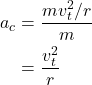
Just as with centripetal force, centripetal acceleration always points to the center of the circular path.

In the video below, Dr. Pasquale rotates a cup of water vertically around in a circle, swinging it around over her head. The tension she applies to the string (which is apparent in Figure 8.9, left, with the string being held very taut) keeps the platform and cup moving in that circular path. The centripetal force points toward the center of the circle. So what keeps the water in the cup? What stops it from spilling out over Dr. Pasquale’s head (see Figure 8.9, right)?

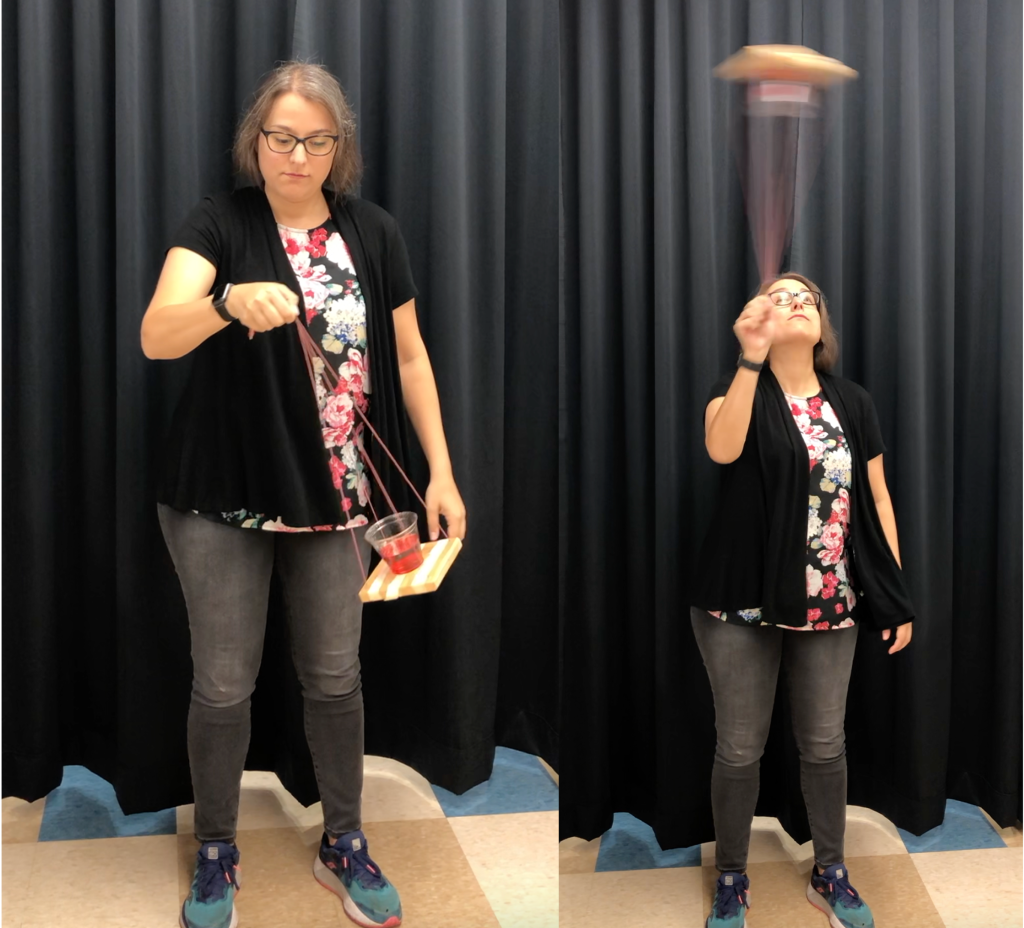
Two side-by-side photographs of Dr. Pasquale, a white lady with brown hair and glasses. On the left, she is holding a sling holding a cup as it is positioned at the bottom of a vertical circular path. On the right, she is holding the same sling while it is positioned at the top of a vertical circular path. There is water in the cup, dyed red. In both photographs, the water is situated in the bottom of the cup. In the background of both photographs is a black curtain.
Figure 8.9 – Dr. Pasquale spins a cup of dyed water on a platform in a vertical circular path. The applied force to the string creates the rotational motion (left), and the inertia of the cup prevents the water from spilling out when the cup is upside-down (right). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Why doesn’t the water spill onto the floor and all over Dr. Pasquale’s head? The answer is inertia. The position of the water in the cup wants to stay where it initially was. So as long as the apparatus is rotated quickly enough, the inertia is going to keep the water firmly planted in the cup.

How fast is fast enough? We need to make sure that the centripetal acceleration of the water is greater than the acceleration due to gravity (9.8 m/s2). In this example, the string and platform have a length of 0.46 m, which is equivalent to the radius of the rotational motion. One rotation is completed in 0.63 s. The tangential velocity is

    \begin{align*} v_t &= \frac{2\pi(0.46~\textrm{m})}{0.63~\textrm{s}}\\ &= 4.59~\textrm{m/s}. \end{align*}

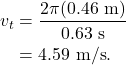
Using this tangential velocity, we can calculate the centripetal acceleration as

    \begin{align*} a_c &= \frac{(4.59~\textrm{m/s})^2}{0.46~\textrm{m}}\\ &= 45.75~\textrm{m/s}^2. \end{align*}

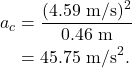
This is indeed larger than the acceleration due to gravity. In fact, it is 4.67 times stronger than the acceleration due to gravity (4.67 “g’s”).

Further reading

  • “Dancing” t-handle in zero g – Watch a video of a T-handle as it rotates about its intermediate axis, causing the rotation to be unstable. (An object that spins about its longest or shortest axis is stable, rotation along the intermediate axis is unstable.)
  • Dorothy Hamill scratch spin – Watch as Dorothy Hamill starts spinning slowly and speeds up when she decreases her angular inertia. This demonstrates the conservation of angular momentum.

Practice questions

Conceptual comprehension

  1. Why is a doorknob typically located as far as possible from the hinges of a door (see Figure 8.10)?
A photograph of an office door. On the left side of the door are three hinges, and on the right side of the door is the doorknob. The hinges and doorknob are both labeled.
Figure 8.10 – A photograph of an office door. On the left side of the door are three hinges, and on the right side of the door is the doorknob. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Numerical analysis

  1. A blade of a ceiling fan completes 120 rotations in one minute. Calculate the rotational speed of the fan in units of…
    1. …RPM (rotations per minute).
    2. …rotations per second.
    3. …degrees per second.
    4. …radians per second.
  2. Vinyl records were commonly used to play music in the mid-20th century. A long-playing vinyl record would rotate at 33 ⅓ revolutions per minute, and would typically have a diameter of 25 cm. What is the rotational speed of this record? What is the tangential velocity at the outer rim of this record?
  3. A bicycle wheel has a radius of 0.35 m and is rotating at 60 RPM (revolutions per minute). Calculate the tangential velocity of a point on the outer rim of the wheel.
  4. Compact discs (CDs) were commonly used to play music in the late 20th century. A CD has a diameter of 12 cm, and rotates such that the tangential velocity remains constant at 1.2 m/s. What is the rotational speed of the CD when playing from its outer rim? What is the rotational speed when playing from a point halfway between the center and outer rim?
  5. A wrench is used to tighten a bolt with a force of 40 N at a distance of 0.2 m from the bolt. Calculate the torque applied to the bolt.
  6. A seesaw is 4 m long and has a person with a mass of 60 kg sitting 2 m from one end. How far from the other end should a person with a mass of 80 kg sit to balance the seesaw?
  7. A force of 13 N is applied at an angle to a wrench. If the lever arm is 0.4 m, calculate the torque produced, if 5 N of the force is applied parallel to the lever arm, and 12 N of the force is applied perpendicular to the lever arm.
  8. A car with a mass of 1,200 kg is traveling around a curve with a radius of 50 m at a speed of 20 m/s. Calculate the…
    1. …centripetal force required to keep the car traveling in that circular path.
    2. …centripetal acceleration of the car.
  9. A 0.5 kg ball is attached to a string and swung in a horizontal circle with a radius of 1 m. If the tension in the string is 10 N, calculate the…
    1. …centripetal force acting on the ball.
    2. …centripetal acceleration of the ball.

Hands-on experiments

  1. If you have a hammer, hold the hammer by the head and rotate it back and forth as many times as you can in 5 seconds. The rotational inertia is low because the mass is concentrated at the center of rotation (your hand). Then, hold the hammer by the end of the handle and rotate it back and forth as many times as you can in 5 seconds. The rotational inertia is much higher now because the mass is concentrated away from the center of rotation. Which orientation was harder to rotate? Why is that?
  2. Use the concept of torque to find the most and least efficient ways to open a door. Start by applying forces as close to the rotational axis as possible (near the hinge), and then try applying forces in the center of the door and finally as far from the rotational axis as possible (near the outer edge of the door, presumably near the doorknob). Which force application was the easiest to open the door? Which was the hardest? Why? Then try applying the force at different angles. Apply a force directly perpendicular to the door’s motion. Then try applying the force at different angles. Finally, open the door and apply a force parallel to the door and observe if it is possible to cause the door to rotate with a force applied in that manner.
  3. Note: the following experiment should only be attempted if you have a space that’s easy to clean, or won’t be damaged by the possible spill of soda. It’s very easy to accidentally spill soda during this demonstration! If you have access to a can of soda, try to reproduce the demonstration where the can is able to be tilted on the lip between the base and sides without falling over (see Figure 8.8). (If you don’t like drinking soda, or are worried about drinking too much of it, pour the soda into a different container so you can pour some back in the can if the CG becomes too low.)

definition

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book