2. Newton’s first law
Summary
Inertia
Newton’s first law is sometimes referred to as the law of inertia, as it describes this property of matter. Newton’s first law says that an object in motion tends to stay in motion, and an object at rest tends to stay at rest, unless acted upon by an outside force.
Inertia describes how difficult it is to change the motion of an object. If an object is at rest, inertia relates to how hard it is to get the object to start moving. If an object is moving in a straight line at a constant speed, inertia relates to how hard it is to get the object to speed up, slow down, or change its direction.
Consider the three objects shown in Figure 2.1. They appear to have similar shapes and sizes. How could we determine the inertia of each object? If inertia relates to the difficulty of getting something to change its motion, then we can figure out which, if any, of these objects has the most inertia by picking each one up and measuring the difficulty in getting each object to move.

In the video below, Dr. Pasquale holds a piece of styrofoam and shakes it back and forth as many times as she can in five seconds. This object was not too difficult for her to move around: Dr. Pasquale was able to move it back and forth 14 times in five seconds.
In the next video (below), Dr. Pasquale will move a clay brick back and forth as many times as she can in five seconds. This brick was more difficult to move than the styrofoam. It had a greater resistance to changes in motion, meaning that it has more inertia. Dr. Pasquale was able to move it back and forth seven times in five seconds.
Finally, in the third video (below), Dr. Pasquale will repeat the experiment one more time with the last object, a piece of lead. This object was very difficult to move. In fact, it was hard even for Dr. Pasquale to pick it up from the cart it was sitting on. She was able to move the lead brick back and forth only two times in five seconds.
What is the difference between the three objects? What property of matter makes the styrofoam easy to move and the lead hard to move? It can’t be volume, because the sizes are all the same. The difference is in the mass of the objects.
The tablecloth trick is a great demonstration of inertia. In the video below, you can watch Dr. Pasquale perform this demo. A table setting consisting of a plate, bowl, glass, vase with a flower, napkin, and silverware is placed on a silk tablecloth. This setup, viewed from top-down, is shown in Figure 2.2. Dr. Pasquale very quickly pulls the tablecloth out from under the table setting.

After Dr. Pasquale quickly pulled the tablecloth out from under the objects, most of the objects stayed put. The top-down view of the table setting after the tablecloth was removed is shown in Figure 2.3. The plate, the flower, and the glass of water pretty much stayed where they were. However, there was a little bit of force present that made the silverware move around a little bit. Inertia relates to the mass of an object. The silverware has the least amount of mass, so it makes sense that they would be the most affected by this demonstration.

Inertia tells us that unless a force acts on an object to change its motion, it will keep doing what it was already doing. While we have not yet formalized the concept of forces, for the purposes of this discussion, a force is nothing more than a push or a pull. Perhaps you are aware of the force of gravity. Gravity acts on each of the objects sitting on the table: the plate, the silverware, the flower in the vase, and the glass of blue water. A support force counteracts gravity and holds each object up.
When the tablecloth is very quickly removed, no new forces are being applied to any of the objects, other than the tablecloth itself. Gravity and the support forces are still present, and there is not much, if any, horizontal force present when the tablecloth is pulled out. Therefore, most of the objects stay put.
Inertia does not only apply to objects that are at rest. It also applies to objects in motion. An object in motion will continue moving in a straight line at a constant speed unless acted upon by an outside force.
In the video below, a ballistic cart contains a small yellow ping-pong ball. As the cart moves past a trigger on the track, it launches the ball into the air. Because the ball and the cart were both moving at the same horizontal speed when traveling together, they will continue to move at the same horizontal speed even if they are separated. Unless a force acts on either object to slow it down or speed it up horizontally, the object will continue moving at the same horizontal speed. After launching into the air, the ball and cart have the same horizontal speed. That means that once the ball comes back down again, it will land right back into the cart. While the ball is in the air, the downward force of gravity does act to change the motion of the ball, but only in the vertical direction. On the way up, gravity acts to slow the ball’s vertical motion. On the way down, gravity acts to speed up the ball’s vertical motion.
This relates to the motion of any objects that are moving together. If you are riding in a train car on a flat straight track, you could throw something straight up in the air and expect to catch it straight back down, as long as the train doesn’t speed up or slow down while the object is in the air.
However, if the train speeds up after you throw a ball into the air, the ball will continue moving at its initial horizontal speed as the train goes faster. The ball will land behind where you initially threw it. If the train slows down after you throw a ball into the air, the ball will land ahead of where you initially threw it.
Inertia also helps to explain why we wear seatbelts in cars. If we are riding or driving in a car, then we are moving at the same speed as the car. If the car is stopped abruptly by an outside force, our bodies naturally want to continue moving at the same speed in the same direction. Without a seatbelt, a collision with another object could cause us to be thrown out of the windshield of a car. Even braking a car very forcefully could otherwise cause us to move forward dangerously out of our seats if we didn’t have a seatbelt on. Seatbelts are important safety devices that prevent that from happening. They apply a force to us to ensure that we slow down or stop moving when the car abruptly stops.
Mass
Mass is a property of physical objects that relates to relates to inertia (resistance to changes in motion). Mass relates to how much “stuff” is in an object. Mass has a symbol of the lowercase letter ![]() , and we use the unit kilograms (kg).
, and we use the unit kilograms (kg).
It’s important to understand that, for most physical objects, mass is a characteristic that does not change. It does not change over time, and it does not change based on where the object is located: the Earth, the Moon, Jupiter, or in the vacuum of space.
The styrofoam brick shown in Figure 2.1 and demonstrated in the video above has a mass of 0.04 kg, the clay brick has a mass of 2 kg, and the lead brick has a mass of 12 kg. Those masses would be exactly the same if they were to be measured on another planet. The inertia of these objects is independent of their location.
The situation for humans is a little different. Our mass can change, but that’s because we eat, exercise, cut our hair, and otherwise do things that may cause our mass to fluctuate. However, if we could somehow keep our mass at a constant value, that number would not change if we then traveled to the Moon, or to Mars, or to any planet or celestial body with a different gravitational force than the Earth.
In other words, while mass is related to a concept called weight, it is a fundamentally different thing! Mass has to do with our resistance to changes in our motion – our inertia. Weight is a force that comes about due to gravity.
Force
Simply put, a force is a push or a pull that causes an object to change its motion. The symbol we use for force is the capital letter F. Because force is a vector, it will either appear symbolically with bold font (![]() ) or with an arrow over the top (
) or with an arrow over the top (![]() ). A vector is a quantity that contains both a magnitude and a direction. That means that the direction in which a force is applied is just as important as how strong the force is.
). A vector is a quantity that contains both a magnitude and a direction. That means that the direction in which a force is applied is just as important as how strong the force is.
Read more!
Appendix A in this textbook contains a full description of vectors, including how they are represented and drawn. It also describes how to add vectors both graphically and numerically. If you are not already familiar with using vectors, read Appendix A before moving along in this textbook.
The units used for force are newtons (N). A newton is a unit that has other units “hidden” inside it. A newton is equal to a kilogram times a meter divided by a second-squared:
![]()
It is possible to use either of these units to express force, but it’s much easier to use the unit of newton, which is why it is used so often in physics.
Forces are used to overcome inertia and make an object change its motion. The amount that an object changes its motion due to a force is the topic of Newton’s second law.
It can be difficult to get a full appreciation for the concept of inertia, as we experience so many forces while living on the planet Earth. Gravity and friction constantly impact the motion of objects on this planet. When you push something, it eventually comes to rest. That may seem to go against the law of inertia, but it doesn’t. By accounting for all of the forces acting on an object’s motion, we can really start to appreciate Newton’s first law.
Right now, as you are reading or listening to this textbook, there are forces acting on you. One of those forces is gravity. Gravity is a force that pulls you toward the surface of the Earth. Another force that is acting on you is a support force from the floor, or chair, or bed, or whatever surface you are sitting, lying, or standing upon. The support force holds you up and prevents you from falling to the center of the Earth. These two forces are likely in perfect balance with each other, which is why you are probably not accelerating either up or down right now (unless you happen to be jumping at the moment!).
Mechanical equilibrium
By analyzing the sum total of all forces acting on an object, we can determine whether or not that object will experience a change in its motion. When the sum of all of the forces acting on an object is equal to zero, then that object is said to be in mechanical equilibrium.
In physics, we use the capital Greek letter Sigma (![]() ) to define “the sum of.” Therefore,
) to define “the sum of.” Therefore, ![]() means “sum of all forces.” We can add together each force to calculate that sum. Sometimes we call this quantity the net force.
means “sum of all forces.” We can add together each force to calculate that sum. Sometimes we call this quantity the net force.
Mechanical equilibrium defines a condition in which the sum of all forces acting on an object is zero. So by saying that the net force is zero, we are saying that the sum of all forces is zero. When the net force on an object is zero, that object is in mechanical equilibrium. As a result, the object will have a constant velocity. That is, the object will have a constant speed along a straight line.
Mathematical representation of mechanical equilibrium
Mechanical equilibrium is achieved when an object has no net force acting on it. That can be mathematically represented using the notation in the following equations:
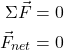
There are two types of mechanical equilibrium: static equilibrium and dynamic equilibrium. Static equilibrium defines a condition of mechanical equilibrium where an object is at rest. The velocity remains constant at zero.
Static equilibrium
In Figure 2.4, a cart sits at rest on a flat, low-friction track. There are forces acting on the cart, but they are completely balanced, and because the cart is not moving, it will continue to not move unless that condition of equilibrium is disturbed somehow by a push or a pull.

The two forces acting on the cart are gravity, which pulls the cart to the Earth, and a supporting force from the track, keeping it in position on the track. These two forces are equal to each other, and point in opposite directions. Therefore, the net force is zero and the cart is in static equilibrium.
Dynamic equilibrium
Dynamic equilibrium defines a condition of mechanical equilibrium where an object moves at a constant nonzero velocity.
In the video below, a cart has been pushed until it travels at a constant speed along a low-friction track. After Dr. Pasquale’s hand stops pushing the cart, the only two forces acting on the cart are gravity and the support force, which remain equal and opposite, creating a net force of zero. This means that the cart will continue to move at the same speed, in the same direction. (In reality, a very small friction force between the wheels and track, as well as a force of air drag as the cart pushes through the air molecules surrounding it, will cause the cart to slow down over time.)
Another example of dynamic equilibrium would be an airplane flying in a straight line at cruising altitude at a steady speed (by using autopilot, for example). Forces in the vertical direction (gravity and the lift) are equal in magnitude and opposite in direction and cancel out. Forces in the horizontal direction (an applied force from the engine and the forces of friction and air drag opposing the motion of the airplane) will also cancel out.
Without a force that propels an object to keep it in motion, it can be difficult to experience a condition of pure dynamic equilibrium on Earth. That’s because there are usually always other forces we have to contend with, notably air drag and friction. By minimizing those forces as much as possible, we can get close to a situation of dynamic equilibrium.
Practice questions
Conceptual comprehension
- Let’s say you were to push against a parked car. The push exerts a large force, but not enough to make the car move. Because the car is not moving, it is in mechanical equilibrium. Is your push the only force acting on the car? If not, what other forces can you identify that are acting on the car?
- Look around you and identify at least five items that are in static equilibrium. What are all of the forces acting on those items?
- As you go throughout your day, identify as many objects that you can that are in dynamic equilibrium. What are all of the forces acting on those objects?
Numerical analysis
- A box sitting on a flat surface has a gravitational force of 10 N and a support force of 10 N. What is the magnitude of the net force acting on the box? Is the box in mechanical equilibrium?
- A person rowing a boat in water exerts a force of 45 N to get the boat to speed up. Drag from the water exerts a force in the opposite direction of 15 N. What is the magnitude of the net force acting on the boat and its occupants? Is the boat in mechanical equilibrium?
- An object has three forces acting on it. A force of 8 N pushes to the right, a force of 3 N pushes to the left, and a force of 2 N pulls upward. Draw a picture of all of the forces. What is the overall horizontal component of the net force? What is the overall vertical component of the net force? What is the magnitude of the net force?
- An airplane has four forces acting on it. There is 4500 N of lift (up), 4000 N of weight (down), 500 N of thrust (forward) and 100 N of drag (backward). Draw a picture of all of the forces. What is the overall horizontal component of the net force? What is the overall vertical component of the net force? What is the magnitude of the net force?
Hands-on experiments
- Place a marble in the center of a plate on a flat surface. Try to tilt the plate to make the marble move. Observe how the marble tends to stay in place until you apply an external force to the plate.
- Place a piece of cardstock paper (or cardboard) over the opening of a cup and put a coin on top of it. Swiftly flick the paper out from under the coin. The coin should fall into the glass because of its inertia. This is demonstrated in the video below.
- Place a piece of paper (or a dollar bill) over the opening of a glass bottle and put a coin on top of it. Remove the paper as quickly as possible from under the coin. The coin should stay on the top of the bottle because of its inertia. This is demonstrated in the video below.
Newton’s first law is sometimes called the law of inertia. Newton’s first law states that “an object in motion tends to stay in motion, and an object at rest tends to stay at rest, unless acted upon by an outside force.”
A scientific law is a statement that describes relationships among the quantities that we observe or measure.
A force is a push or a pull that causes an object to change its motion. More fundamentally, force is an interaction between two objects. (symbol: F, unit: N)
Inertia is a property of matter whereby objects resist changes in their motion. Inertia is related to the mass of an object.
Speed is the scalar quantity that describes the rate at which an object changes its position. Speed is equal to position divided by time. (symbols: s, |v|, unit: m/s)
Mass is a property of physical objects that relates to resistance to changes in motion: inertia. (symbol: m, unit: kg)
Gravity is the attractive force experienced by objects of mass. It is one of the four fundamental forces.
The weight of an object is proportional to its mass as well as the force of gravity acting on that object, related by Newton's second law. More accurately, weight arises due to a supporting force acting on the object.
A vector quantity is a variable that must be conveyed with both a numerical quantity (indicating magnitude or strength) and a direction.
Physics is a branch of science that focuses on the fundamentals of the workings of our universe.
Newton's second law states that the acceleration of an object is proportional to the net force acting on the object, and inversely proportional to the mass of the object. In equation form, Newton's second law can be stated as F_net = ma.
Mechanical equilibrium is a condition where the net force and net torque acting on an object are equal to zero. Two cases of mechanical equilibrium are static and dynamic. An object in mechanical equilibrium has a constant velocity (constant speed in one direction).
The net force is the vector sum of all forces acting on an object.
Velocity is the vector quantity that describes the rate at which an object changes its position. Velocity is equal to displacement divided by time. (symbol: v, unit: m/s)
Static equilibrium is a special case of mechanical equilibrium where both the velocity and rotational speed of an object are constant and equal to zero.
Dynamic equilibrium is a condition of mechanical equilibrium where either the velocity or rotational velocity of an object is constant and not equal to zero.

