31. Light quanta
Summary
At this point, this textbook has provided some convincing evidence that light exhibits many wave-like properties. It can interfere, it can diffract, and it can be polarized.
This chapter will take that understanding of light and turn it on its head. What if light isn’t only a wave, but also a particle? Hopefully this chapter will show you how light can be treated as both a particle and a wave in different situations. In fact, both the wave and particle aspects of light are necessary in order to formulate a complete understanding of light. The quantum nature of light is truly fascinating!
Quantum physics
By the end of the 19th century, humankind had developed what is known as classical physics. Classical physics describes the natural phenomena we’ve discussed so far in this textbook: physics that uses Newton’s laws of motion, Maxwell’s equations, and the laws of thermodynamics. These laws seemed to form a complete understanding of how the universe worked in terms of particles and waves.
While some mysteries (such as the spectral distribution of incandescence and the observation of ultraviolet light ejecting electrons from metals) remained, these were expected to be soon resolved with a proper application of the classical laws.
At this same time, scientists began to make other startling discoveries. These included the discovery of x-rays, radioactivity, and the electron. Attempts to explain these new observations with laws of classical physics failed. Classical physics led to very deep contradictions between what the laws predicted and what was experimentally observed.
It should be stated at the onset that the classical laws of physics work very well for objects that are larger than atoms and molecules. We have seen a lot of convincing evidence for this so far in this textbook! The strange new effects that were observed occurred when doing science on a very small scale: light interacting with small particles such as atoms, protons, or electrons.
What was needed was a new set of physical laws to explain the observed experimental results that occur on a very small scale. This led to the quantum revolution. We call these new laws quantum physics.
Of course, any new scientific theory has to also account for the correct predictions of the old theory. That is, in addition to explaining new experimental observations, the new theory has to also explain observations for all the situations in which the old theory was valid. This notion was put forth by Niels Bohr in the early 1920s and is called the correspondence principle. The correspondence principle requires that quantum physics and classical physics produce the same result when quantum physics is applied to large-scale objects.
At the heart of quantum physics is the concept that properties that we consider to be continuous on the macro (large) scale become quantized when things become extremely small. A quantity that is quantized is something that only takes on certain well-defined values. For example, the number of people in a room is a quantized property. There can be a room filled with 40 people, or 28, but not four and a half people. The number of pennies in a jar is quantized, as is the number of atoms in a person, the charge of an atom, or the energy of electrons in an atom (as discussed in the previous chapter of this textbook).
The idea is that quantum physics can be used to explain all phenomena: those happening on the very small scale as well as those happening on a very large scale. However, because quantum physics is so mathematically complicated, and because classical physics works so well on the macro scale, there is no need to use quantum physics when calculating quantities on the macro scale. Because quantum equations will produce the same results as Newton’s laws (for example), using Newton’s laws is perfectly sufficient when calculating velocity, acceleration, momentum, and other kinematic quantities for any interaction that is large enough for us to see with our eyes.
It’s also important to point out that the theoretical models we currently use to understand the universe, whether it be quantum physics, Newtonian physics, or general relativity, are excellent models that have undergone rigorous scientific inquiry and scrutiny. But that doesn’t mean that these models are not subject to adjustment and change as we learn more about the universe. Either way, the correspondence principle dictates that any modifications must still yield the same results for situations where the previous theory worked.
This chapter focuses on quantum physics as it pertains to light in particular. The next chapter of this textbook will expand on this for a more general discussion on quantum phenomena.
Wave-particle duality
At this point, we have seen some convincing evidence that light is a wave. Light can undergo diffraction, interference, and polarization. These are all phenomena that would not happen if light was not a wave. Furthermore, the fact that light can be polarized indicates that light is a transverse wave.
The photoelectric effect
In 1905, Albert Einstein published a paper describing a phenomenon that had an astounding implication: that light acts not like a wave, but like a particle! This paper was on the photoelectric effect, and his explanation of this effect was the reason that Einstein received a Nobel prize in 1921.
The photoelectric effect is the emission of electrons when light of a particular frequency (especially UV light) strikes a metal target. By itself, this observation was not groundbreaking. It is the details of how the photoelectric effect works that upended our understanding of classical physics and the treatment of light as a wave.
In this video below, a piece of zinc has been loaded up with electrons by rubbing it with a charged piece of PVC. Placing the zinc on the electroscope visually demonstrates the presence of these electrons. When Dr. Pasquale shines a UV light source on the zinc, electrons are ejected from the metal. We can tell that this occurs because the electroscope rapidly goes back to its neutral state.
Classical physics predicts that energy is transferred from the light wave to the electron. It predicts that when a sufficient amount of energy is built up, an electron will eventually be emitted from the metal. This predicts that the intensity of light would be the indication of electron ejection. Strong light would eject electrons quickly, and dim light would eject electrons with a time delay as the electrons gradually build up more energy.
We can test this classical prediction by taking that same piece of negatively charged zinc and illuminating it with a bright white light source. If the classical model were correct, this would also cause the zinc to quickly eject the electrons and cause the electroscope to relax back to its neutral state. This is demonstrated in the video below. When Dr. Pasquale turns on a bright light source, which is much brighter than the relatively dim UV source used earlier, there is no change in the presence of electrons. No matter how long she waits, the electroscope remains negatively charged. (At the end of the video, Dr. Pasquale removes the excess negative charges by grounding the electroscope.)
These results must have another explanation. The classical model does not hold up here.
A summary of the classical predictions and the observed experimental results for the photoelectric effect (the ejection of an electron after monochromatic light is absorbed by a metal) is provided in the table below.
|
classical predictions |
experimental results |
|
The kinetic energy of the ejected electrons should increase when light of greater intensity is used. |
The kinetic energy of the ejected electrons is the same regardless of the light intensity. |
|
The kinetic energy of the ejected electrons should not be affected by the frequency of the light. Only the intensity of the light should affect the kinetic energy. |
The kinetic energy of the ejected electrons decreases to zero at a threshold frequency, below which no electrons are ejected, regardless of the light intensity. |
|
Dim light should require a longer time for electrons to be emitted (because more time is needed for the electrons to acquire the needed energy to escape). |
Although fewer electrons are ejected, there is no measurable time delay when using dim light compared to bright light. |
Einstein proposed that the results of the photoelectric effect could be easily explained by treating light as though it interacted with the metal in discrete bundles or quanta of energy. These packets of electromagnetic energy later became known as photons. (It was not until 1926 that the term photon was coined.) In short, a photon is a particle of light.
Quantum theory predicts that the intensity of the light does not matter: the frequency of the light does. Each individual photon that hits the zinc has energy given by Planck’s constant times the frequency (recall 
from the previous chapter). In this manner, bright light at frequencies that are lower than a threshold energy will never cause electron ejection, which is what we observed when shining bright white light on the zinc. Each photon of white light was incapable of ejecting an electron, as white light is composed of frequencies of light that are lower than that of UV light.
Similar to the photoelectric effect is the photovoltaic effect. The photovoltaic effect occurs when a photon hits a material and causes an electron to become excited such that it can now give rise to electric current. The photovoltaic effect is used to generate electric power in solar panels.
Both the photoelectric and photovoltaic effects indicate that light is a particle. But effects such as interference and polarization indicate that light is a wave. This is known as wave-particle duality. Wave-particle duality is the concept that something like light is both a wave and a particle. Both wave and particle descriptions are required to accurately depict quantum phenomena such as light. Generally speaking, when light travels through space, it acts like a wave. When light interacts with matter, it acts like a particle.
Asking if light is a particle or a wave is like asking if a spork (Figure 31.1) is a fork or a spoon: it’s both! So is light: both a wave and a particle.
As Einstein stated: “It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do.”
Matter waves
In 1924, Louis de Broglie, a French graduate student, pondered that if entities that we typically consider to be waves can act like particles, perhaps it is possible that entities that we typically consider to be particles can act like waves. In 1929, de Broglie won the Nobel prize for his hypothesis after the first experimental evidence for the wave nature of electrons was obtained by Clinton Davisson and Lester Germer in 1927.
As with all quantum properties, this effect (particles acting like waves) is only noticeable on a very small scale. Macroscopically, the wave-like nature of particles is a negligible effect that we can ignore without affecting the outcome of our experiments or calculations. On the atomic scale, the wave-like nature of particles cannot be ignored.
We use the de Broglie equation to calculate the wavelength of matter waves. The de Broglie equation states that
The wavelength of the matter wave is equal to Planck’s constant divided by the momentum of the object.
Consider a macroscopic object: a 150 gram baseball, thrown at a fast pitch of 45 meters per second. First we can calculate the momentum of the baseball. Remember that momentum equals mass times velocity, and we need to be careful that our mass is expressed in units of kilograms. The momentum of the baseball is
The wavelength of the baseball is Planck’s constant divided by this momentum. It can be calculated as
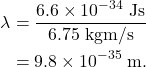
Considering that a baseball has a diameter of 7.25 cm (0.07 m), the size of the wavelength of the baseball is essentially zero compared to the size of the baseball itself. This wavelength compared to the size of the baseball is roughly the same as comparing the size of an atomic nucleus to that of the Milky Way galaxy! In short, the wavelength of the baseball is so small that we will never notice its wave-like effects such as diffraction or interference.
Now let’s consider an electron, a decidedly subatomic object. An electron has a mass of 
, and for this example we can assume that it travels at 1% of the speed of light. The momentum of the electron will therefore be
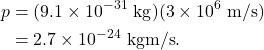
The wavelength of the electron is Planck’s constant divided by the momentum, which is 
, or 0.24 nm. While this is definitely a small number, it is equivalent in length scale to the wavelength of x-rays. And considering that the diameter of an entire atom is about the same size, the wavelength of an electron is definitely noticeable on this length scale. In fact, it is the wave behavior of the electrons that give atoms their size! (An atom does not have a rigid boundary or structure to it; the size of an atom is therefore defined by the distance between the nucleus and the extent of the wave motion of the electrons, a concept known as the atomic radius.)
All of this discussion leads to further questions. When we speak of matter waves, what exactly is oscillating? How do these waves propagate? Even de Broglie himself did not know. This will be addressed in the next chapter of this textbook.
The double-slit experiment
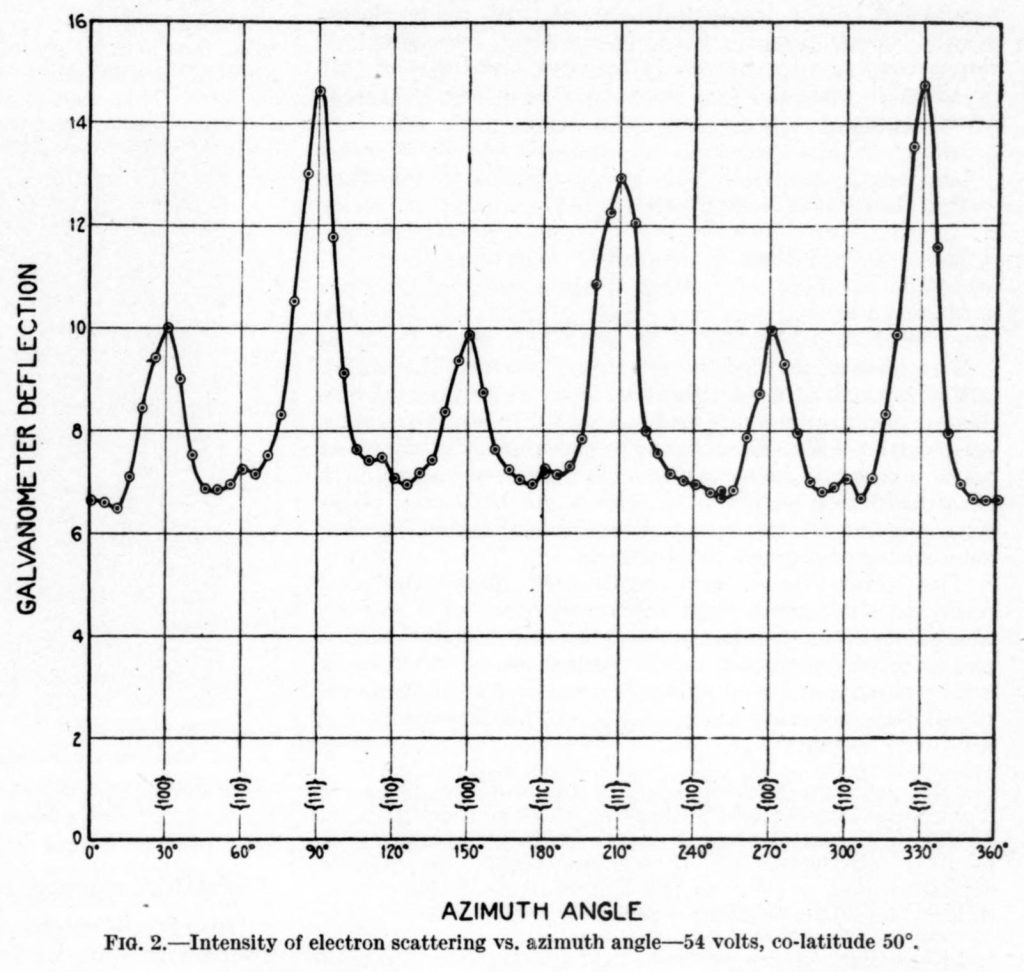
What experimental evidence might convince you that subatomic particles such as electrons act like waves? The Davisson–Germer experiment confirmed the wave-like nature of electrons. This experiment measured a diffraction pattern generated by electrons as they were scattered by a periodic crystal structure (which acts in a similar manner to a diffraction grating).
The data measured in this experiment is shown in Figure 31.2, which plots the current (which is proportional to the number of electrons hitting a screen some distance away from the periodic crystal) on the y-axis and the scattering angle on the x-axis. The data demonstrates a diffraction pattern, which would not occur if the electrons acted as particles instead of waves.
Recall that diffraction of waves occurs any time those waves travel through a narrow opening. If there are two small openings, this will lead to an interference pattern that arises due to a mixture of diffraction from each slit and interference, leading to bright and dark spots on a screen some distance away.
Diffraction experiments have shown that even when a light source is so low that single photons are sent through a double slit one at a time, the interference pattern continues to be observed on a screen some distance away. It should be pointed out that it is not that the entire interference pattern flashes with each photon. Rather, the individual photons hit the screen as particles and make small dots. It is only after recording the individual dots of each photon that we see the development of the interference pattern. This is an effect that cannot be explained using classical models of physics.
If objects that are completely particle-like are sent through one or two slits, we would likely expect that they would create an image that resembles the size and shape of the opening, somewhat like spraying paint through a stencil.
It turns out that when electrons are sent through a double slit, they also generate a wave-like interference pattern when measured some distance past the double slit. This is not what we would expect if electrons only acted like particles. And just as with single-photon experiments, when electrons are shot through the double slit one at a time, they will, over time, create an interference pattern. Not only do electrons act like waves, but they do so in a way that cannot be explained by classical physics. This effect is demonstrated in the video below, which shows the accumulation of multiple electrons on a sensor. Over time, the interference pattern created by the electrons’ wave-like nature becomes clear.
The uncertainty principle
Hopefully by now you’re convinced that all objects are wave-like, and that this wave-like property is especially pronounced on the scale of the subatomic. Inherent in all wave-like systems is the uncertainty principle, which theorizes the extent to how well we can know information about related properties. This is not a limitation of current technology, but a fundamental property of wave-like systems.
For example, position and momentum are linked in uncertainty. The uncertainty principle between these two quantities can be expressed as an equation:
where uncertainty is represented by the capital Greek letter delta, followed by the symbol used for the variable that there is uncertainty in. The quantity
where 
is Planck’s constant.
To illustrate this, consider a long train of waves such as shown in Figure 31.3 (top). This wave appears to have a very well-defined wavelength. If the wave represented a matter wave of some particle, we could use the de Broglie equation to find that this particle has a very well-defined momentum. However, the wave is spread over a very wide region of space. In other words, the position of the particle represented by this wave can be anywhere since the wave is so spread out.
On the other hand, consider the wave pulse shown in Figure 31.3 (bottom). In this case, the location of the wave appears to be localized in a small region of space. For a matter wave of this shape, the position of the particle represented by this wave is well-defined. However, because there is not a well-defined wavelength, the momentum cannot be measured precisely.
Suppose you wanted to track the trajectory of a subatomic particle such as an electron. In order to “see” the electron, you need to shine light on it. However, the individual photons striking the electron can and do alter the original behavior of the electron. You could use low-energy photons to do this so that you would not alter the momentum of the electron very much. However, low-energy photons have a long wavelength. This means that there will be a greater spread in the uncertainty of the position of the electron. If you want to be more precise in determining the position of the electron, you will need to use light that has a shorter wavelength. However, photons that have a short wavelength have a higher frequency and therefore carry more energy. These photons will give the electron a bigger kick and therefore create greater uncertainty in the momentum of the electron.
This exchange is unavoidable. It is a fundamental property of wave-like systems that there is a lower limit with which the precision that complementary variables (such as position and momentum) can be measured. Because the product of both uncertainties has a lower limit, there is a limit to the precision of any measurements we can make on these two properties. If you know the position of something with a high level of accuracy, then the accuracy with which you can measure momentum will be limited. To the extreme: if you know with perfect certainty the exact location of a wave, then it is impossible to know the momentum of that wave, and vice versa. The uncertainty can never be zero for both quantities simultaneously.
Two other complementary properties that are linked in uncertainty are energy and the time at which the object had that energy. We can state that uncertainty in these two variables as
In order to measure the energy of a particle, we need to track it. To do this, we could measure the time it takes to travel a certain distance. Since the particle is spread out in space due to its wave-like properties, tracking it for a short time does not give a very precise measure of that distance. Therefore, the energy cannot be determined precisely. To get a more precise measure of the energy, we have to allow the particle to move through space for a longer time. Again, this exchange cannot be avoided. The more precisely we measure one variable, the more imprecisely the complementary variable can be determined.
It’s important to point out that uncertainty doesn’t just exist on the quantum scale, but also on the macro scale. However, because 
is so small, this effect is trivial for most objects we can see with our eyes. If you wanted to track the trajectory of a ball thrown through the air, you would still need to observe the light reflecting off the ball into your visual receptors. In this case, the interaction of the individual photons striking the ball will not alter the trajectory of the ball in any significant way. That is, the light does not affect macro-scale experiments in any noticeable way.
Further reading
- Bach, R., Pope, D., Liou, S.H., & Batelaan, H. (2013). Controlled double-slit electron diffraction. New Journal of Physics, 15(3), 033018. https://doi.org/10.1088/1367-2630/15/3/033018
- The double-slit experiment – This article from Physics World magazine explains a double-slit experiment conducted with electrons.
Practice questions
Numerical analysis
- Calculate the wavelength of an Olympic sprinter having a mass of 94 kg who completes a 100 m run in 9.58 seconds.
- Calculate the wavelength of a cyclist who, along with her bicycle, has a mass of 100 kg and rides at a speed of 11.2 m/s.
- Calculate the wavelength of an ice hockey puck with a mass of 160 g moving at a speed of 51 m/s.
- Calculate the wavelength of an electron having a mass of 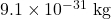and a speed of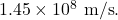
- Calculate the wavelength of a neutron having a mass of
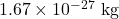and a speed of 2290 m/s. - Calculate the wavelength of a helium atom having a mass of
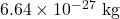and a speed of 1780 m/s. - Calculate the wavelength of a sodium atom having a mass of
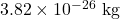and a speed of 870 m/s.
Classical physics describes the natural phenomena that can be explained by Newton’s laws of motion, Maxwell’s equations, and the laws of thermodynamics.
Physics is a branch of science that focuses on the fundamentals of the workings of our universe.
Thermodynamics is the study of heat flow and its relationship to temperature, work, energy, and entropy.
A scientific law is a statement that describes relationships among the quantities that we observe or measure.
A wave is a periodic oscillation that transfers energy from one place to another.
Incandescence is a form of light emission and heat transfer process by which an object emits electromagnetic radiation with a peak frequency that corresponds to the temperature of that object.
An electron is a fundamental building block of matter that has a negative charge and is found surrounding the nucleus of an atom.
Radioactivity is the process by which an unstable nucleus releases energy and emits a particle.
Science is the systematic pursuit of knowledge that comes about through asking questions, making careful observations, and carrying out experiments about how the universe works.
A proton is a subatomic particle that has a positive charge and resides in the nucleus of an atom.
Quantum physics describes the physical laws used to describe the properties of matter and energy that occur on a very small scale.
A theory is an explanation of how the universe works that is supported by multiple, repeated experiments.
Electric charge is a fundamental property of matter that causes particles that carry a charge to experience a force when in the presence of an electric field.
Energy is defined as the capability of an object (or collection of objects) to do useful work. (symbol: E, unit: J)
Velocity is the vector quantity that describes the rate at which an object changes its position. Velocity is equal to displacement divided by time. (symbol: v, unit: m/s)
Acceleration quantifies the rate at which an object changes its velocity. (symbol: a, unit: m/s^2)
Momentum is a vector property that quantifies the motion of an object. It is sometimes called "inertia in motion" as it is the product of mass and velocity. (symbol: p, unit: kgm/s or Ns)
Diffraction is a bending of a wave as it travels around a corner or through a narrow opening.
Interference is the phenomenon that occurs when two waves overlap. The total amount of wave energy present at a point is equal to the sum of each individual wave's energy at that point.
Polarization is the property of transverse waves which allows them to have their electric field components oscillating in a single direction.
In a transverse wave, the vibrations of the wave travel perpendicular to the direction of motion of the wave.
The photoelectric effect is the emission of electrons when light of a particular frequency (especially UV light) strikes a metal target.
Frequency describes how many oscillations occur per second in a wave. (symbol: f, unit: Hz)
Intensity describes the amount of energy per unit of area that reaches a certain location every second (unit: W/m^2)
Grounding is a special type of conduction where charges redistribute themselves to an area that can accept lots of charges without causing a large buildup of electrons or positive ions.
Current describes the flow of electric charge through a circuit. (symbol: I, unit: A)
Power quantifies how quickly work is done. (symbol: P, unit: W)
A hypothesis is a proposed explanation of how the universe works that is based on observations and can be tested experimentally.
The wavelength of a wave describes the shortest distance between two identical repeating points on a wave. (symbol: λ, unit: m)
Mass is a property of physical objects that relates to resistance to changes in motion: inertia. (symbol: m, unit: kg)
Scattering is a process where the direction that a wave travels in is changed without affecting the wavelength.
The uncertainty principle theorizes the extent to how well we can know information about related properties.
Technology is the outcome of using scientific principles to solve problems. This can be a product, innovation, or other object whose creation is based on science such as physics, chemistry, or biology.
