10. Projectile and satellite motion
Summary
Projectile motion
Projectile motion describes the motion of an object that moves in free fall. That is, the only force acting on the object is gravity. Remember that free fall is an ideal scenario that ignores dissipative forces such as friction and air drag. The study of objects that travel like this is known as ballistics.
Ballistics (the physics of projectile motion) allows us to understand and quantify the motion of things such as baseballs after they leave the bat, rockets that are only powered internally very briefly before coming back to the Earth’s surface again, as well as the motion of planets, other celestial bodies, and artificial satellites.
In the simplest scenario, an object can be thrown straight up so that it moves in a completely vertical path. That’s the scenario we’ve already discussed in chapter three of this textbook. Alternatively, an object can be thrown upward, but at an angle to the horizon. This gives the object both vertical and horizontal motion.
In the absence of air drag and friction (which will be assumed unless otherwise stated), the only force that acts on an object during projectile motion is gravity. Gravity only works in the vertical direction. To understand how the horizontal motion of the projectile works, we must remember Newton’s first law: inertia. The projectile will continue to move at the same speed in the horizontal direction, even while the vertical speed changes due to gravity. Fortunately, we can do an analysis of the horizontal motion separately from the analysis of the vertical motion.
In the video below, two identical steel balls are launched from a platform at exactly the same time. One is dropped in a completely vertical manner, and the other is pushed, giving it horizontal motion in addition to the vertical drop.
Both of the balls hit the surface of the lab table at exactly the same time, indicating that gravity acted on the objects in an identical manner. The ball that had horizontal motion did not exhibit any effects in its vertical motion, which means that the horizontal motion for this ball did not affect its vertical motion.
Fortunately, we are able to independently calculate the horizontal and vertical motion of a projectile in free fall. This will enable us to determine what equations we can use to analyze the motion in each direction. Each of the forces and related kinematic constants and equations (acceleration, velocity, and distance) are listed in the table below.
|
direction |
force |
acceleration |
velocity |
displacement |
|
horizontal |
none |
0 m/s2 |
|
|
|
vertical |
gravity |
-9.8 m/s2 |
|
|
In the horizontal direction, there are no forces at work on the object. Because of this, the law of inertia tells us that the object will continue moving with the same speed in the horizontal direction. As an equation, this is expressed as: ![]() , the velocity of the projectile at any moment in time is equal to the initial velocity. Because there is no accelerating force, the distance the object moves horizontally can be analyzed using the equation
, the velocity of the projectile at any moment in time is equal to the initial velocity. Because there is no accelerating force, the distance the object moves horizontally can be analyzed using the equation ![]() : displacement equals velocity times time.
: displacement equals velocity times time.
In the vertical direction, the force acting on the object is gravity. The acceleration due to gravity is -9.8 m/s2. (Remember that the negative sign indicates that the force and acceleration point down.) Because there is acceleration at work, the equations of motion in the vertical direction will be different from the equations in the horizontal direction.
The vertical velocity of the projectile at any given moment in time is equal to ![]() , which is the initial velocity plus acceleration (due to gravity) times time. The displacement that the object moves vertically can be analyzed using the equation
, which is the initial velocity plus acceleration (due to gravity) times time. The displacement that the object moves vertically can be analyzed using the equation ![]() . It is important to note that the equations of non-accelerated motion cannot be used when there is a force acting on an object!
. It is important to note that the equations of non-accelerated motion cannot be used when there is a force acting on an object!
In the video below, a ballistic cart launches a ping-pong ball directly upward with no horizontal motion. The ball moves upward as it slows down (vertically) under the influence of gravity. It stops for a brief instant of time as it turns around and moves back down to the cart, speeding up (vertically) as it does so. This is a special case of projectile motion: where there is no horizontal motion at all. This type of motion was introduced and discussed in chapter three.
On the other hand, the ballistic cart can launch the ball while it moves with a horizontal velocity. We learned in our discussion of inertia that the ping-pong ball will continue moving at the same horizontal speed, even while the vertical motion of the ball is influenced by gravity. This is why the ball is caught by the cart again as it moves back down to its initial height, shown in the video below.
The shape of the motion of a projectile moving with horizontal and vertical motion is known as a parabola. We can therefore say that a projectile has parabolic motion. A graph of the position of a projectile (qualitatively similar to the ball launched by the ballistic cart) with respect to time is shown in Figure 10.1. Understanding this motion enables scientists and engineers to design rockets, satellites, and other projectiles that have parabolic motion.
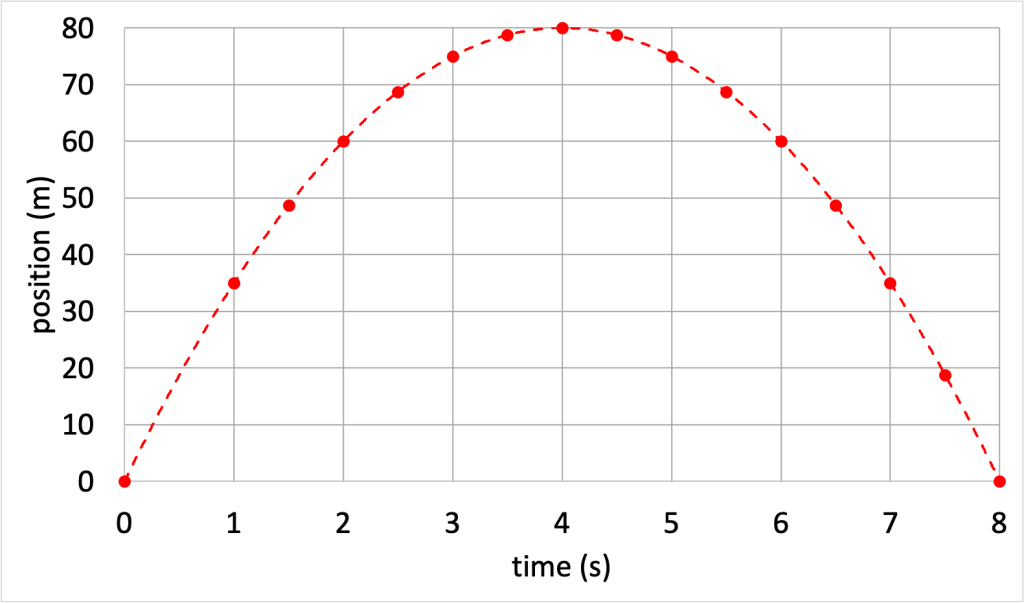
An important takeaway from the video of the steel balls dropping, and the videos of the ballistic cart launches, is that the horizontal and vertical components of motion can be calculated and analyzed independently. This greatly simplifies the study of projectile motion!
When air drag cannot be ignored
It should be noted that when air drag cannot be ignored, the equations describing the trajectory of the projectile are not as simple. This is because the drag force always points in a direction tangent to the trajectory and opposite to the instantaneous velocity at every instant. This means that the vertical and horizontal forces are continuously changing. Therefore, the vertical and horizontal analyses are not independent and must be analyzed simultaneously. Such an analysis is beyond the scope of this textbook.
Maximizing horizontal range
Because a projectile can be launched at so many different angles with respect to the horizon, what angle would we choose if we wanted a projectile to have the maximum horizontal range?
If we conceptualize the motion of a projectile, an object launched directly upward will spend the most time in the air, but will have the least horizontal motion as it travels in a completely vertical line. On the other extreme, if something were to be launched at just a few degrees with respect to the horizon it would not spend as much time in the air, minimizing its horizontal range. To maximize the horizontal range, we must choose an angle somewhere in between zero and ninety degrees.
In the video below, Dr. Pasquale launched a projectile at fifteen degrees, thirty degrees, forty-five degrees, sixty degrees, and seventy-five degrees with respect to the horizon. Each of the projectiles has an identical initial velocity. In each case, we can look at the parabolic motion of the projectile. Because the initial height of the projectile changes when the launcher is tilted at different angles, we will only consider the motion back to the same starting height, rather than considering the motion back to the height of the table.
As expected, very steep angles maximize the height of the ball, but don’t move much horizontally. Very shallow angles spend less time in the air, causing them to lose out on horizontal motion. At forty-five degrees, we maximize the horizontal range by creating the best tradeoff between time in the air and horizontal motion.
Figure 10.2 shows a graph of the horizontal and vertical positions for projectiles launched at the same angles as in the video. These positions were calculated using the equations of motion. The graph demonstrates the vertical and horizontal ranges of each launch angle. (This data is qualitatively similar to the data shown in the video above, but is not identical due to the small amount of air drag that is present.)
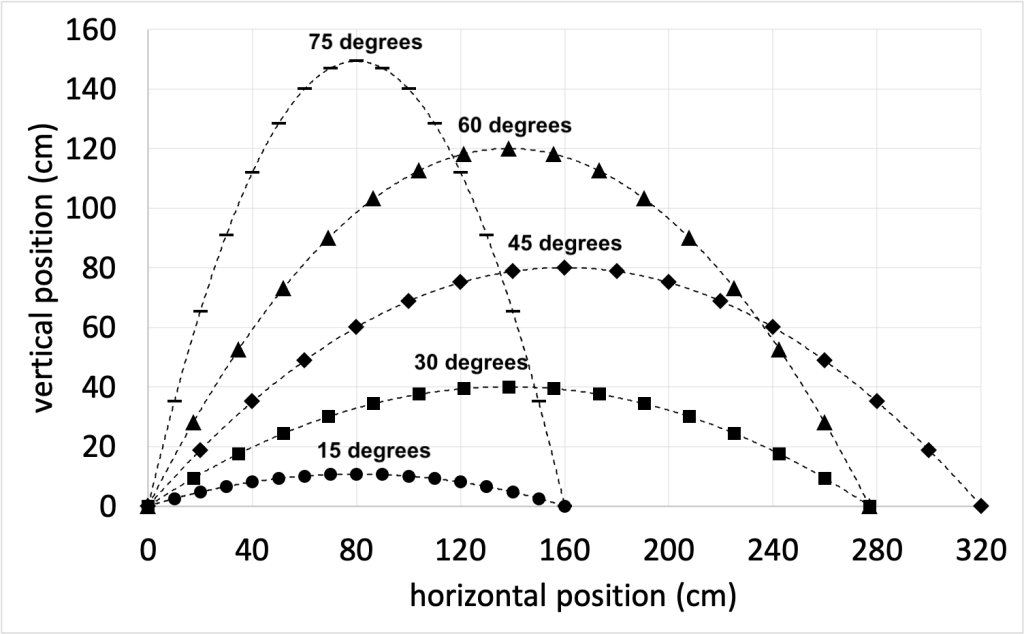
In the absence of air drag, a launch angle of forty-five degrees will maximize the horizontal range of a projectile.
Symmetry of motion
In the absence of forces such as air drag, the motion of a projectile is symmetric both in time and horizontally in space. This means that
- it takes a projectile the same amount of time to go from ground level to the top of its path as it does to go from the top of its path back down to ground level again,
- the vertical velocity of a projectile at the end of its motion when it reaches the ground again is equal and opposite to the initial vertical velocity of the projectile at launch, and
- a projectile moves the same horizontal distance between ground level and the top of its path as it does from the top of its path back down to ground level again.
From the symmetry of motion arises three key moments in the motion of a projectile, which are
- the initial time a projectile is launched,
- the moment the projectile reaches the top of its path, and
- the time the projectile reaches ground level again.
These three key moments act as important times to calculate for different kinematic properties (height or vertical velocity) because there will always be a known variable, simplifying the equations that are used. This information is outlined in the table below.
|
key moment |
time |
vertical position (y) |
horizontal position (x) |
vertical velocity ( |
|
initial launch |
0 |
0 |
0 |
|
|
top of the path |
½ of total time |
maximum height |
½ maximum range |
0 |
|
return to ground level |
total time |
0 |
maximum range |
|
Solving projectile motion equations
The motion of projectiles can be analyzed using the information presented in this and previous chapters of this textbook.
For example, say a projectile is launched from ground level with an initial horizontal velocity of 10 m/s and an initial vertical velocity of 30 m/s. We want to solve for three different quantities:
- How high will the projectile go?
- How long will the projectile stay in the air?
- How far will the projectile travel in the horizontal direction?
The first question asks about height. Because we are interested in the maximum height of the projectile, the key moment is the top of the path of the projectile. We can see from the table above (and recall from many examples in this textbook) that the vertical velocity at that key moment is 0 m/s. The two vertical kinematics equations are

While we eventually want to use the distance equation to solve for height, at this moment we don’t know the amount of time that the projectile travels, so we can’t use the equation yet. However, we can use the velocity equation to solve for the amount of time it will take the projectile to reach the top of its motion (which is, incidentally, equal to one-half of the total time of motion). Because the vertical velocity at this key moment is 0 m/s, we can solve the velocity equation for time.
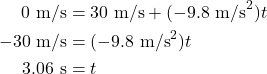
It takes 3.06 s for the projectile to reach the peak of its motion. Now that we know the time, we can plug that value into the vertical distance equation to determine the height, which is
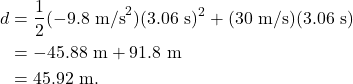
Now we can determine how long the projectile will remain in the air. Based on the calculation of time at the key moment of being at the top of the path, we know that the projectile takes 3.06 s to complete one half of its total motion. Because the motion is symmetric, if it takes 3.06 s to get up, it will take another 3.06 s to get back down again. So we know that the projectile will spend 6.12 s in the air.
If you are asked to solve for how long the projectile will remain in the air without needing to first calculate the initial height, it’s possible to determine this value by using the key moment of the return to ground level. At that time, the vertical position is zero, and the final vertical velocity is equal to the opposite value of the initial vertical velocity. Use the velocity equation to solve for time.
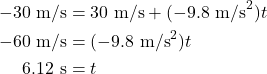
Finally, we can answer the question of how far the projectile moves horizontally. The position of maximum horizontal range occurs at the key moment of the return to ground level. We know from previous calculations that it takes the projectile 6.12 s to reach that key moment. Now we can use the equations of horizontal motion (no acceleration) to calculate the horizontal range.
![]()
Satellites and orbits
A satellite is a projectile that falls around the Earth, rather than falling back down to its surface. A thought experiment may help to conceptualize what this means. Consider that Jason Q. Physics builds an extremely tall tower, possibly several kilometers high, and stands at the top with several baseballs. Assuming that Jason has enough oxygen to survive this experiment, he can throw the baseballs at various speeds and see what happens.
This thought experiment is animated with a video, below. (Note: the video is not to scale!) To start, Jason drops a baseball. It falls straight down to the Earth’s surface in a vertical line. If he now gives the ball a gentle throw in the horizontal direction, it will still fall to the Earth’s surface, but the motion gives it a gentle curve. As he throws the remaining baseballs faster and faster, the baseball will travel a greater distance along the Earth’s surface. At some point, we can no longer ignore the curvature of the Earth’s surface. Eventually, the trajectory of the motion of the baseball will match the curvature of the planet. That trajectory is known as an orbit. An orbit describes the curved path that a satellite takes as it moves around an object of mass. In that case, Jason Physics has turned the baseball into a satellite!
When we were dealing with baseballs near the surface of the Earth, the force of gravity (both magnitude and direction) was considered constant: 9.8 m/s2, vertically downward. For the baseballs launched from Jason Physics’ tower, the gravitational force varies in magnitude (weaker at higher altitudes) and direction (points toward the center of the Earth). When these factors are considered, the resulting trajectory of the orbit becomes elliptical in shape.
At what speed must the baseball be thrown to obtain this satellite motion? We can turn to rotational motion to calculate an exact answer. The centripetal force of the satellite must be supplied by gravity. Set the centripetal force equation equal to Newton’s law of universal gravitation, and solve for velocity.

In this equation, ![]() is the orbital velocity (the minimum velocity required to obtain orbit around the Earth).
is the orbital velocity (the minimum velocity required to obtain orbit around the Earth). ![]() is the radius of the satellite’s orbit (this is equal to the radius of the Earth plus the orbital height of the satellite).
is the radius of the satellite’s orbit (this is equal to the radius of the Earth plus the orbital height of the satellite). ![]() is the universal gravitational constant, and
is the universal gravitational constant, and ![]() is the mass of the Earth. (If you wanted to place a satellite in orbit around a different celestial body, you would simply use the mass and radius of the celestial body you wish to orbit.)
is the mass of the Earth. (If you wanted to place a satellite in orbit around a different celestial body, you would simply use the mass and radius of the celestial body you wish to orbit.)
This equation can be used to calculate the orbital velocity of the international space station, which orbits approximately 400 km above the Earth’s surface. The mass of the Earth is ![]() , and the radius of the Earth is approximately 6400 km. The orbital velocity therefore equals
, and the radius of the Earth is approximately 6400 km. The orbital velocity therefore equals
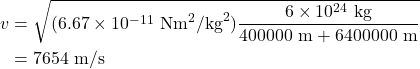
The orbit of a satellite describes its path around a planet or star. All closed orbits are elliptical. A special case of an elliptical orbit is the circular orbit. The above baseball example, and calculations for the international space station, described circular orbits.
In a circular orbit (shown in Figure 10.3, left), the height above the Earth’s surface remains constant. Considering the conservation of mechanical energy, because the orbital height remains constant, the GPE is constant throughout the satellite’s motion. Because mechanical energy is conserved, the KE must also remain constant, causing the speed of the satellite to remain the same throughout its motion.

In an elliptical orbit, a satellite will orbit around a planet or a star, with the planet or star at one of the focal points of the ellipse. As the satellite moves, the distance away from the planet or star changes (Figure 10.3, right). Mechanical energy is conserved. This means that as the GPE decreases, when the satellite is closest to the planet, the KE will increase, and vice versa. Therefore, when the satellite is closest to the planet, it will be moving at the fastest speed. When the satellite is farthest from the planet, it will be moving at the slowest speed.
Kepler’s laws of planetary motion
The discovery of elliptical orbits came about in the early 1600s thanks to Johannes Kepler, before Newton published his theory on universal gravitation. Kepler was an apprentice of Tycho Brahe, a Danish astronomer, who made very accurate observations of the positions of stars and planets over a span of decades in the late 1500s (without the aid of a telescope). Kepler used Brahe’s data and plotted the orbit of Mars from the vantage point of someone looking down on the solar system from above. Kepler tried to use the equation of a circle to fit the points along the orbit and found that he couldn’t. He was only able to fit the orbital path if he used the equation for an ellipse rather than a circle. The discovery that planets orbit in ellipses rather than circles is the first of what became known as Kepler’s three laws of planetary motion.
Kepler’s first law
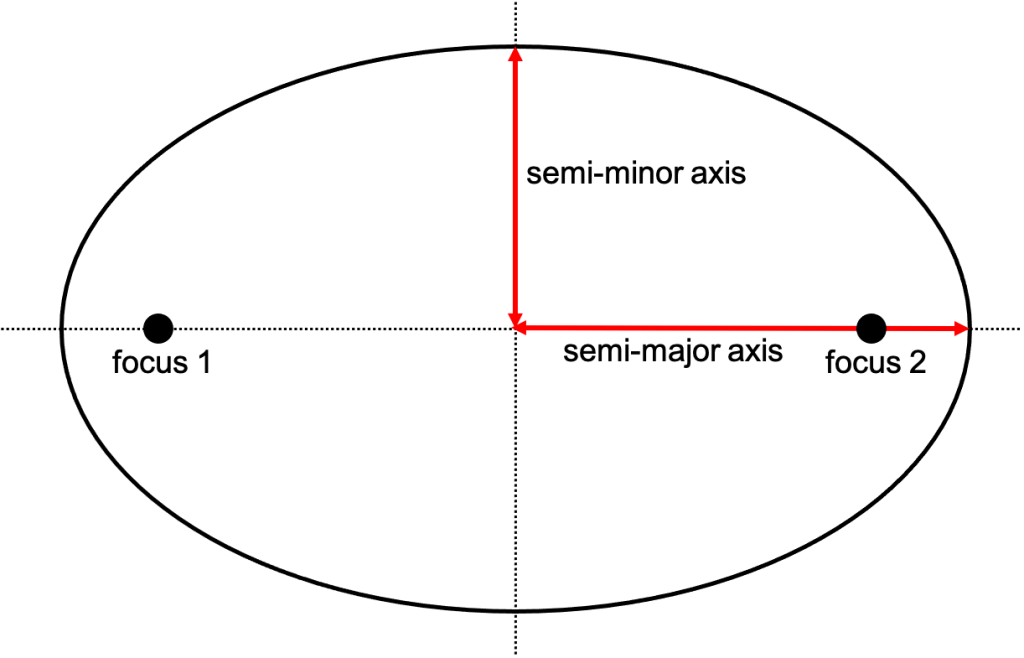
Kepler’s first law of planetary motion (the law of orbits) states that planets orbit their sun in ellipses with the sun at one focus of the ellipse (such as the orbit shown in Figure 10.3, right). This law is valid for any satellite in a closed orbit around a host body, whether it be a planet around a star or a moon around a planet. It should be noted that circular orbits are possible. A circle is just a special case of the ellipse in which the two foci are at the same point (Figure 10.3, left).
Kepler’s second law
Kepler’s second law of planetary motion (the law of areas) states that the position vector of the planet relative to its sun will sweep out equal areas in equal time intervals. As seen in Figure 10.4, the planet takes a certain time (![]() ) to move from point A to point B. When the planet is at point C, it will move to point D in the same time interval (
) to move from point A to point B. When the planet is at point C, it will move to point D in the same time interval (![]() ). The areas of region ABO and region CDO are the same.
). The areas of region ABO and region CDO are the same.

This turns out to be a consequence of the conservation of angular momentum. While the mathematical details are too involved for this textbook, a qualitative description is warranted. Like the figure skaters who pull in their arms and legs to minimize their rotational inertia to make themselves rotate faster, the planet’s rotational inertia about the sun is smaller when it is close to the sun. When the planet is farther away, its rotational inertia is greater because its mass is farther from the center of rotation (the sun). This increase in rotational inertia causes the rotational speed around the sun to decrease. Thus, the planet moves faster when closer to its sun and slower when farther away from its sun.
Kepler’s third law
Kepler’s third law of planetary motion (the law of periods) states a mathematical relationship between the time it takes for the planet to complete one orbit (the orbital period) and the semi-major axis of the elliptical orbit (see Figure 10.5).
Specifically, the relationship states that the square of the orbital period is directly proportional to the cube of the semi-major axis: ![]() . For a circular orbit, the semi-major axis just becomes the radius of the circle. With just a little effort, Kepler’s third law can be easily shown for a circular orbit (see the textbox below for the derivation). We start by recognizing that the gravitational force is responsible for the centripetal force that produces the circular motion.
. For a circular orbit, the semi-major axis just becomes the radius of the circle. With just a little effort, Kepler’s third law can be easily shown for a circular orbit (see the textbox below for the derivation). We start by recognizing that the gravitational force is responsible for the centripetal force that produces the circular motion.
Since the motion is circular, the gravitational force is producing a centripetal force as described in chapter 8. We then equate the gravitational force between the planet (m) and its sun (M) separated by a distance r (![]() ) to the centripetal force (
) to the centripetal force (![]() ), where v is the orbital speed of the planet. Recalling that speed is the path divided by time, the orbital speed is just the circumference of the circle divided by the orbital period. That is,
), where v is the orbital speed of the planet. Recalling that speed is the path divided by time, the orbital speed is just the circumference of the circle divided by the orbital period. That is,
![]()
After plugging the above equation for speed into the expression for the centripetal force, we can solve for ![]() . The result is
. The result is
![]()
Since ![]() ,
, ![]() , and
, and ![]() are all constants, this proves the relationship that
are all constants, this proves the relationship that ![]() . Note that the mass of the planet (
. Note that the mass of the planet (![]() ) doesn’t affect this relationship because it cancels out in the derivation.
) doesn’t affect this relationship because it cancels out in the derivation.
Derivation of Kepler’s third law
Orbital speed, ![]() , is equal to path divided by time (
, is equal to path divided by time (![]() ). For a circular orbit, the path is equal to the circumference of the circle:
). For a circular orbit, the path is equal to the circumference of the circle: ![]() . This value will be plugged into the above equation for
. This value will be plugged into the above equation for ![]() to continue the derivation.
to continue the derivation.
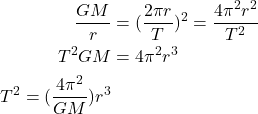
As an example, a planet that is four times farther from its host star will have an orbital period that is eight times greater, since ![]() .
.
Practice questions
Numerical analysis
- A ball is launched vertically upward from the ground with an initial speed of 10 m/s. Calculate…
- …the time it takes the ball to reach its maximum height.
- …the maximum height of the ball.
- A soccer ball is kicked horizontally from a height of 2 meters above the ground with an initial horizontal speed of 15 m/s. Calculate…
- …how far the ball travels horizontally before hitting the ground.
- …the vertical speed of the ball immediately before impact.
- …the horizontal speed of the ball immediately before impact.
- …the total magnitude of the ball’s velocity immediately before impact.
- A baseball is thrown with an initial horizontal speed of 20 m/s. It lands on the ground 4 seconds later. Calculate…
- …how far the ball travels horizontally before hitting the ground.
- …the height the ball falls in that time.
- …the vertical speed of the ball immediately before impact.
- …the horizontal speed of the ball immediately before impact.
- …the total magnitude of the ball’s velocity immediately before impact.
- A rock is dropped from a bridge into a river below. If it takes 3 seconds to hit the water, how high is the bridge above the water’s surface?
- A rocket is launched from the ground with an initial vertical velocity of 30 m/s upward and a horizontal velocity of 40 m/s. Calculate…
- …the time it takes for the rocket to hit the ground.
- …the horizontal distance traveled by the rocket.
- A satellite with a mass of 500 kg is in a circular orbit around Earth at an altitude of 500 km above the surface. The tangential speed of the satellite is 7615 m/s. Calculate its kinetic energy, gravitational potential energy, and total mechanical energy. Note: for questions 6, 7, and 8, you will have to use the equation
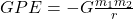 for GPE. Refer to the section in chapter 9 referring to gravitational potential energy in nonuniform gravitational fields. Refer to Appendix B for information such as the mass of the Earth.
for GPE. Refer to the section in chapter 9 referring to gravitational potential energy in nonuniform gravitational fields. Refer to Appendix B for information such as the mass of the Earth. - A communication satellite (1,000 kg) is in a geostationary orbit around Earth at an altitude of approximately 35,786 km. (That is, the satellite orbits at the same speed as the rotation of the Earth around its axis.) Calculate the kinetic energy, gravitational potential energy, and total mechanical energy of the satellite.
- A satellite (2,500 kg) is in an elliptical orbit around the Earth. As it moves from an altitude of 200 km to an altitude of 400 km, calculate…
- …the GPE of the satellite at both altitudes.
- …the change in ME as the satellite moves from low to high altitude.
- …the change in KE as the satellite moves from low to high altitude.
Hands-on experiments
- Crumple a piece of paper into a ball and set up a target (e.g., a trash can or a box) on the floor. Stand a fixed distance away from the target and try to toss the paper ball into the target. Experiment by changing the angle and force of your toss to observe how it affects the distance and accuracy of your throw.
Free fall is defined as a situation where gravity is the only force acting on an object. Forces such as friction and air drag are ignored and assumed to be equal to zero. The acceleration of an object in free fall is defined by the acceleration due to gravity (g).
A force is a push or a pull that causes an object to change its motion. More fundamentally, force is an interaction between two objects. (symbol: F, unit: N)
Gravity is the attractive force experienced by objects of mass. It is one of the four fundamental forces.
Ballistics is the study and analysis of how projectiles travel.
Physics is a branch of science that focuses on the fundamentals of the workings of our universe.
Path describes the total distance that an object travels as it moves from one point to another, measured along its trajectory. It is a scalar quantity. (symbols: d, x [for horizontal path], y [for vertical path], unit: m)
Newton’s first law is sometimes called the law of inertia. Newton’s first law states that “an object in motion tends to stay in motion, and an object at rest tends to stay at rest, unless acted upon by an outside force.”
Inertia is a property of matter whereby objects resist changes in their motion. Inertia is related to the mass of an object.
Speed is the scalar quantity that describes the rate at which an object changes its position. Speed is equal to position divided by time. (symbols: s, |v|, unit: m/s)
Acceleration quantifies the rate at which an object changes its velocity. (symbol: a, unit: m/s^2)
Velocity is the vector quantity that describes the rate at which an object changes its position. Velocity is equal to displacement divided by time. (symbol: v, unit: m/s)
Displacement describes the straight-line distance from one point to another. Displacement is a vector quantity. (symbols: Δd [for general displacement], Δx [for horizontal displacement], Δy [for vertical displacement]. unit: m).
The orbit of a satellite describes its path around a planet or star.
Centripetal force is a force, pointing toward the center of the rotational motion of an object, that causes an object to move in a circular path. (symbol: F_c, unit: N)
Mass is a property of physical objects that relates to resistance to changes in motion: inertia. (symbol: m, unit: kg)
Mechanical energy is the sum of kinetic energy and potential energy of a system. When ignoring dissipative forces such as air drag and friction, mechanical energy will be conserved.
A theory is an explanation of how the universe works that is supported by multiple, repeated experiments.
A vector quantity is a variable that must be conveyed with both a numerical quantity (indicating magnitude or strength) and a direction.
Rotational inertia is a measure of how much an object resists changes to its rotational speed.
Rotational speed quantifies how quickly (or slowly) something rotates about an axis. (symbol: ω, unit: RPM, degrees/s, rad/s, etc.)

