18. Thermodynamics

Summary

Thermodynamics is the study of heat flow and its relationship to temperature, work, energy, and entropy. Thermodynamics has huge relevance in our lives, as it explains the workings of and constraints of all heat engines, from power plants to internal combustion engines to refrigerators and HVAC systems.

The laws of thermodynamics play a large role in how scientists and engineers develop efficient power generators and motors. The concept of entropy is always present in our lives, as we find that it’s easier to create disorder than order.

Absolute temperature scales

In thermodynamics, absolute scales are important. This is because an absolute scale is established based on a physical limit to how cold things can get. This physical limit establishes the zero end of the scale. The Kelvin scale is an absolute temperature scale. Zero kelvin is equal to absolute zero: the coldest possible temperature.

The Kelvin temperature scale was developed so that a change in one kelvin is equal to a change in one Celsius degree. This makes conversion between Celsius and Kelvin scales a matter of simply adding and subtracting. Zero K is equal to -273 oC. Therefore, to convert from Celsius to kelvin, add 273. To convert from kelvin to Celsius, subtract 273.

What evidence do we have that there is an absolute lower limit to temperature? How do we know that absolute zero exists?

Experiments establishing the relationship between the temperature of a substance and the volume of that substance were performed in the 1700s. As the temperature increased, volume increased. By extrapolating this data, it is possible to see a temperature at which the volume of the substance would be equal to zero. This is shown in a graph in Figure 18.1.

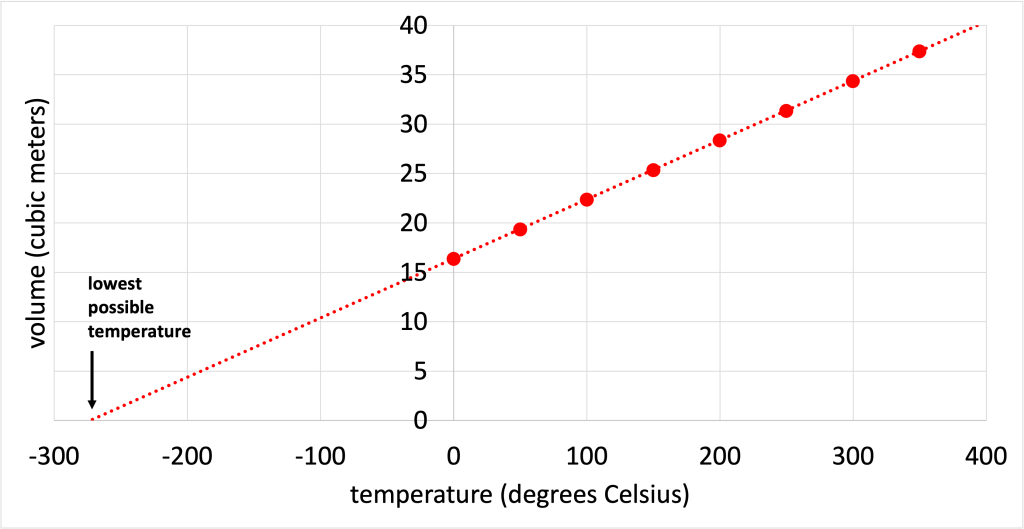
A graph with volume (cubic meters) on the y-axis and temperature (degrees C) on the x-axis. 9 data points are plotted showing a linear relationship between these two variables for a hypothetical substance. A linear fit line is shown extrapolating to inersect at -273 degrees C when the volume is zero.
Figure 18.1 – A graph depicting the relationship between temperature and volume of a hypothetical substance. The point at which the volume would be zero is the lowest possible limit to temperature (absolute zero). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

This establishes a physical limit to the system: it is not possible to have zero volume, and certainly not possible to have a negative volume. Experiments on other substances found a similar relationship. That is, different gases showed a linear volume vs. temperature graph that, when extrapolated to zero volume, led to the same temperature. This temperature is known as absolute zero.

Scientists have been able to achieve extremely low temperatures, to within less than a billionth of a degree of absolute zero. To our current level of knowledge, actually achieving absolute zero is not possible. This is because it would take an infinite amount of work to remove all of the heat from a substance. Absolute zero is more of an asymptotic limit than an actually attainable temperature.

The first law of thermodynamics

The first law of thermodynamics is nothing more than conservation of energy with the inclusion of thermal energy. In a closed system, the first law of thermodynamics can be stated in equation form:

    $$\Delta E = Q - W.$$

\Delta E is the change in internal energy of the system, expressed in units of energy (joules or calories). Q is the heat added to the system, also expressed in either joules or calories. W is the work done by the system, also expressed in joules or calories. Emphasis should be placed on the signs of Q and W when performing calculations. Since Q is the heat added to the system, Q will be a negative number if heat is removed from the system. Since W is the work done by the system on its surroundings (such as during an expansion), W will be a negative number if the surroundings do work on the system (such as during a contraction).

Internal energy is the sum total of all of the kinetic and potential energies of the molecules in a system. This is usually related to temperature and phase. If the internal energy of a system is increased by adding heat, and that system does no work, then the molecules in that system will increase their kinetic energy or change their phase.

The first law of thermodynamics tells us that we cannot get energy for free. There is no such thing as a machine that can be made to do work with no energy input. It would violate conservation of energy. Simply put: “we cannot get something for nothing.”

Adiabatic processes

An adiabatic process is a specific type of thermodynamic process in which the heat added to or removed from a system is zero. The system is either very well insulated or the process occurs so quickly that there is not enough time for heat to be added or removed from the system. If work is done ON the system, W will be negative, and the internal energy of the system will increase.

This is demonstrated in the video below. This syringe contains the head of a match. As you can see, the initial state is that the match has not been ignited. First, Dr. Fazzini pushes down slowly on the syringe. This process is not adiabatic; work is done on the gas inside of the syringe, but that heat has enough time to leak through the walls of the syringe, causing the temperature inside to remain relatively constant. The second time, Dr. Fazzini pushes quickly and creates an adiabatic process. When the fire syringe is compressed very quickly with enough force, there is not enough time for heat to leak out of the system. The work done on the system causes the internal energy of the match head to increase to such an extent that the match head ignites and briefly sparks a fire.

This process is used in diesel engines. Internal combustion engines require a mixture of fuel and air to be ignited to create mechanical work. In a gasoline engine, spark plugs are used to ignite that mixture. In a diesel engine, there are no spark plugs. Instead, the work done during the adiabatic compression of the piston in the engine provides the increase in internal energy that causes the ignition of the fuel and air mixture, creating mechanical work output.

The second law of thermodynamics

Before discussing the second law of thermodynamics, it is important to consider the direction that heat will spontaneously flow. Heat will only spontaneously flow from hot to cold. It will never spontaneously flow from cold to hot. This is similar to gravity, which will cause a ball to roll down a hill, but never up. To get something back to the top of the hill, we have to exert energy to do so. Similarly, while heat will not spontaneously flow from a region of lower temperature to a region of higher temperature, that does not mean we cannot make heat flow “uphill.” To get heat to flow from cold to hot, as an air conditioning unit or refrigerator does, external energy input is required. That fact that nature has a preference for the direction in which heat will flow is governed by the second law of thermodynamics.

Consider a metal rod that is hot on one end and cold on the other end at some initial point in time. As time passes, the hot end will cool down and the cold end will warm up until the entire rod is at a common intermediate temperature. The thermal energy flows from the hot end to the cold end. However, the reverse process will never occur spontaneously even though it does not violate conservation of energy. (The greater kinetic energy of the atoms and molecules at the hot end could be gained at the expense of decreased kinetic energy of the atoms and molecules at the cold end. Still, this never happens spontaneously.)

A heat engine (which will be discussed in greater detail in the next section of this chapter) is a device that uses a difference in temperature to do useful work while operating in a cycle. The second law of thermodynamics tells us that not all heat input will be converted to useful work in this process. There will always be wasted heat. So, while the first law of thermodynamics tells us that “we can’t win,” the second law tells us “we can’t break even” either.

In the video below, Dr. Pasquale uses hot and cold water to do useful work in a demonstration of a heat engine. This demo is a very simple model of a factory where widgets come in on one level on a conveyor belt, get raised up to a higher level, and then get moved away to another area of the factory on a second conveyor belt higher up. The heat engine raises the mass (so that it can move along the higher conveyor belt), and then lowers down so a new mass can be placed into the system. By placing the bulb of this heat engine into hot water, the gases inside the bulb warm up and expand, causing the mass to rise up to the second level. While in this demo there is no conveyor belt, much less a whole factory, Dr. Pasquale can use her hand to move the mass elsewhere.

After the first mass has moved along in the model factory, the system is ready for a second mass. How can the system reset back to the lower level? The bulb needs to cool off somehow. It is currently warm, and now Dr. Pasquale must throw away that heat to reset the process. Whether Dr. Pasquale waits for the bulb to cool off in the atmosphere, or cools the bulb by plunging the bulb into cold water, either way, that heat energy does not do any useful work. Instead, it slightly raises the temperature of the surroundings, which does not equate to any useful mechanical process.

Dr. Pasquale repeats this process several times in the demo. Every time she needs to reset the system, heat energy is wasted. This is an inevitable result of physics that is formalized by the second law of thermodynamics.

Heat engines

A heat engine is a device that uses a difference in temperature to do useful work while operating in a cycle. Heat engines are used in many types of power plants: nuclear, coal, and gas turbines heat water into steam to spin a coil of wire around a magnet, generating electricity. Internal combustion engines that use fossil fuels to do mechanical work, especially in automobiles, are heat engines. On a more basic level, the refrigerator in your home is a heat engine operating in reverse.

The drinking bird, shown in the video below, uses a heat difference due to the evaporation of water from the bird’s head. This causes a fluid to flow up into the bird’s head and create a torque that tips the bird. When the bird’s head tips over, fluid is released back into the base of the bird and it tips back upright again. This process will repeat until all of the fluid evaporates.

While the drinking bird is arguably not a terribly useful heat engine, and is certainly a very inefficient heat engine, it produces mechanical work from a temperature difference.

The Stirling engine, shown in the video below, uses a heat source (boiling water underneath the engine) and a cool source (room temperature air above the engine) to expand and compress gas that causes the motion of pistons. Without a temperature difference between the hot piston and the cold piston, gas would not expand or contract, and there would be no mechanical work output.

The video below demonstrates a heat engine known as a Hero’s engine. There is a large flask filled with water placed over an open flame. That flame causes the water to boil, creating steam. The steam releases through openings in the piping. This steam generates a torque that causes the engine to rotate. This rotation is mechanical work.

Note that this demo caused water to splatter out of the openings in the piping, demonstrating really well the concepts of centripetal force and tangential velocity!

Engine efficiency

The measure of how well a heat engine converts thermal energy into useful work is called the efficiency of the engine. To put it simply, the efficiency is just what you “get out” divided by what you “put in.” What you get out is the useful work done by the engine. What you put in is the heat that enters the engine from the high temperature region. That is,

    $$e = \frac{\textrm{work output}}{\textrm{heat input}}.$$

A perfect engine would be one in which all of the entering heat is converted into useful work. Such an engine would be 100% efficient because there would not be any heat expelled into the low temperature region. The second law of thermodynamics tells us that the efficiency of a heat engine can never be 100%. Some of the heat in the system will always be transformed to unusable forms of energy and wasted.

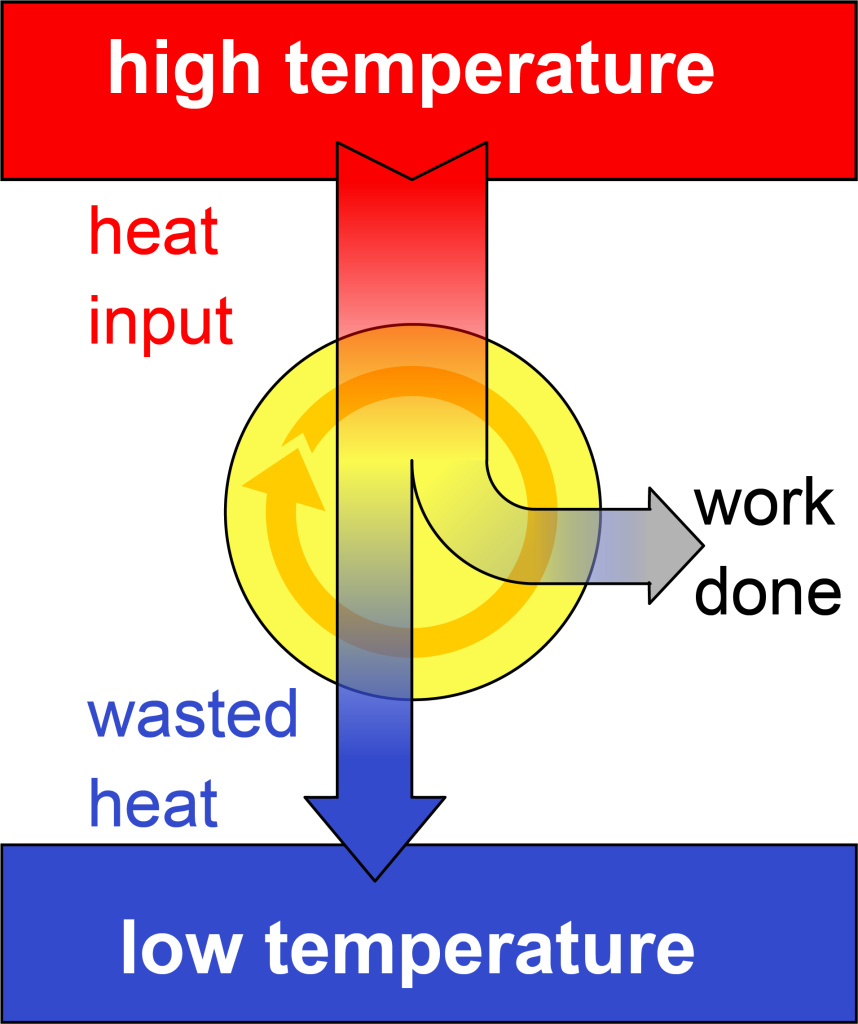
As shown in the video above (demonstrating the simple model of a factory), there must always be heat dumped into the low temperature region in order to reset the engine for the next cycle. This can perhaps be visualized by looking at a block diagram of a heat engine, shown in Figure 18.2. This confirms the conclusion of the second law of thermodynamics, which essentially says that heat input cannot be converted completely into useful work.

A diagram showing heat flowing from hot (red rectangle) to cold (blue rectangle) via a heat engine (yellow circle). The arrow from hot to the heat engine is wide and labeled "heat input." This arrow splits at the heat engine. Some of the arrow points outward and is labeled "work done." The rest of the arrow points downward to the cold area and is labeled "wasted heat."
Figure 18.2 – In a heat engine, useful work can be done due to the difference in temperature between a hot and cold source. However, some heat will be wasted and lost in the process. Heat engine by Alyssa J. Pasquale, Ph.D., (adapted from original work by MikeRun) is licensed under CC BY-SA 4.0.

If the efficiency cannot be 100%, what is the best efficiency that we can have within the laws of physics? This problem was solved by Sadi Carnot in 1824. While the mathematics involved is beyond the scope of this textbook, the result of Carnot’s discovery is that the highest efficiency attainable for any heat engine under ideal conditions (no friction or other losses such as turbulence or unwanted heat transfer) depends only on the absolute temperature of the hot and cold regions. This highest efficiency is called the Carnot efficiency and is equal to the temperature of the hot area minus the temperature of the cold area, all divided by the temperature of the hot area. In other words

    $$e_{carnot} = \frac{T_h - T_c}{T_h}.$$

This equation can be restated as

    $$e_{carnot} = 1 - \frac{T_c}{T_h}.$$

The temperature scale used in this equation must be an absolute scale: Kelvin.

If we look at the equation for Carnot efficiency, the only way the efficiency of a heat engine can be 100%, representing a perfectly efficient heat engine, is if the temperature of the cold area is zero: absolute zero. That isn’t possible, so the efficiency of a heat engine will never be 100%. We can also see from the equation that efficiency can be maximized as much as possible by increasing the temperature difference between the hot and cold areas. If the temperature difference is small, the efficiency will be very low.

The heat engine demonstrating the model factory used hot water at a temperature of 98 oC (371 K) and cold water at a temperature of 10 oC (283 K). To calculate the Carnot efficiency of this heat engine, the temperatures must be expressed in units of kelvin. The Carnot efficiency is calculated below, and is rather small due to the very small difference between temperatures of the hot and cold sources.

    \begin{align*} e_{carnot} &= \frac{371 K - 283 K}{371 K}\\ &= 0.24\\ &= 24\% \end{align*}

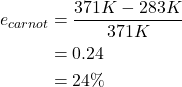
In reality, all real heat engines operating between two given temperatures will always have an efficiency that is less than the Carnot efficiency. This is due to physical limitations of any engine or machine that come about due to friction or other losses.

Refrigerators

If you reverse all the arrows in the heat engine shown in Figure 18.2, you would do work on a system in order to draw heat from a low temperature region and then dump all that energy into a high temperature region (as shown in Figure 18.3). In other words, a heat engine operating in reverse is a refrigerator. A refrigerator is a device that uses work input from an external source to remove heat from an already cold region while operating in a cycle. All the energy that enters the system (W_{input} + Q_{from cold region}) is then expelled into the high temperature region.

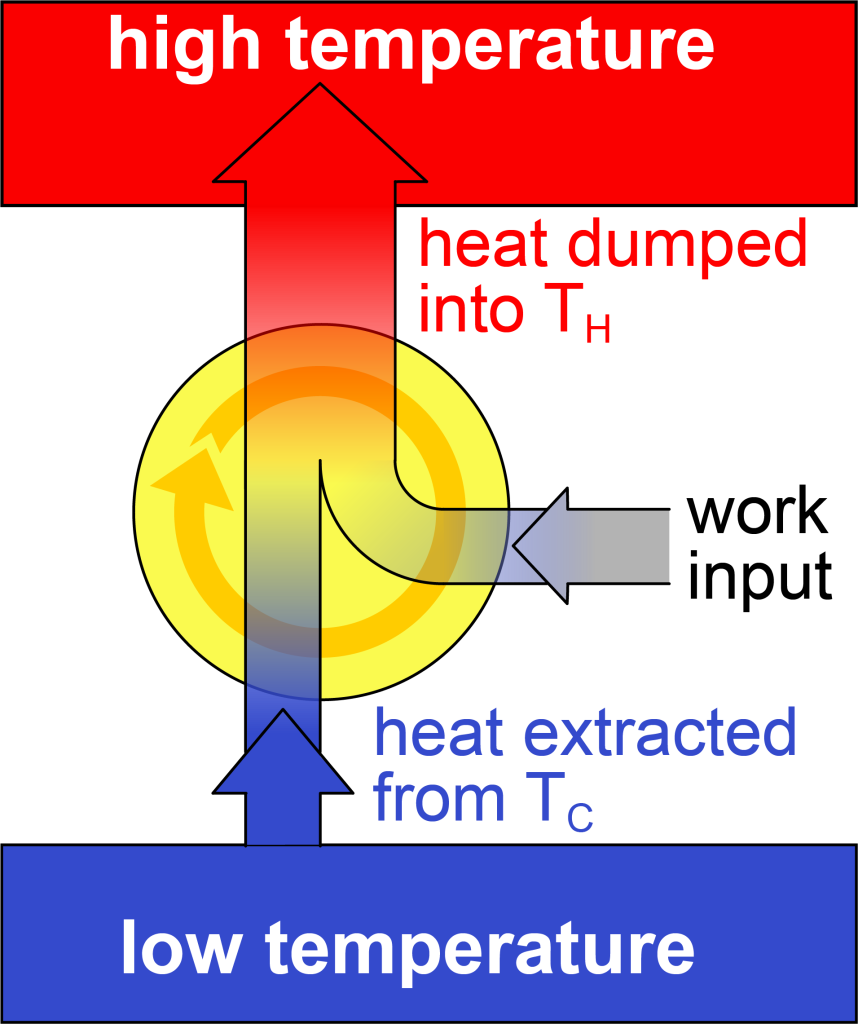
A diagram showing heat extracted from cold (blue rectangle), being dumped into the hot (red rectangle) via a refrigerator (yellow circle). The arrow from the cold is narrow and has an upward pointing arrow labeled "heat extracted from Tc." Into this arrow is input a second external arrow labeled "work input." These two arrows together sum into a wider arrow that goes into the hot part of the refrigerator and labeled "heat dumped into Th."
Figure 18.3 – In a refrigerator, work input can cause heat extracted from a cold region to be dumped into a hot region. Refrigerator by Alyssa J. Pasquale, Ph.D., (adapted from original work by MikeRun) is licensed under CC BY-SA 4.0.

A measure of the refrigerator’s ability to do this is called the coefficient of performance (COP). The symbol for coefficient of performance is the lowercase Greek letter kappa (\kappa). Like the efficiency of a heat engine, COP is also defined as what you “get out” divided by what you “put in.” In this case, however, what you get from the refrigerator is the heat extracted from the low temperature region. What you put in is the work you do to extract the heat from the low temperature region. This equation is

    $$\kappa = \frac{Q_C}{W_{input}}.$$

A perfect refrigerator is one that would require no work to extract heat from the low temperature region. Of course, the net result of such a device would be a spontaneous flow of heat from a cold place to a hot place. As mentioned earlier, the second law of thermodynamics forbids this from happening. There are no perfect refrigerators. Put simply: your refrigerator will not work unless you plug it in!

As with the heat engine, there is an upper limit to how well a refrigerator operating between two temperatures can accomplish its task. The parameter that describes this is the Carnot coefficient of performance (COP). The formula for the Carnot COP is

    $$\kappa_{carnot} = \frac{T_c}{T_h - T_c}.$$

All real refrigerators operating between two given temperatures will always have a COP that is less than the Carnot COP. This is due to the physical limitations of any real machine (friction, drag, and other dissipative forces).

Throughout the ages, humans have been fascinated with the idea of perpetual motion machines. There have always been people who have tried to create a machine that will run forever without any input of energy. The first law of thermodynamics tells us that perpetual motion machines that create energy from nowhere are impossible. The second law of thermodynamics tells us that perpetual motion itself is impossible. For any machine to operate in a closed cyclical loop forever and ever, energy must be continually fed into the system to keep it moving.

Entropy

Entropy describes the amount of disorder in a system. When we consider a system, entropy is related to the number of different states that the system can be in. A simple example of a small system is a single coin. The coin can be either in its heads or tails configuration: two states (Figure 18.4).

A photograph of a US penny heads up (left) and tails up (right).
Figure 18.4 – A single coin has two possible states: heads and tails. States of one coin by Alyssa J. Pasquale, Ph.D., (adapted from US One Cent Coin, public domain, US Mint) is licensed under CC BY-NC-SA 4.0.

When a second coin is introduced into the system, there are now four different states the system can be in: both tails, both heads, and two states consisting of one heads and one tails (Figure 18.5).

Figure 18.5, described in the caption.
Figure 18.5 – Two coins have four possible states: heads/heads, heads/tails, tails/heads, and tails/tails.States of two coins by Alyssa J. Pasquale, Ph.D., (adapted from US One Cent Coin, public domain, US Mint) is licensed under CC BY-NC-SA 4.0.

The more coins that are introduced into the system, the more possible states there are.

A disordered system of multiple coins would be composed of a random arrangement of heads and tails among all the coins. A highly ordered system would be one where all of the coins are the same: all heads up, or all tails up. When the system consists of a single coin, the probability of getting all heads is 50%. When the system consists of two coins, the odds of having all heads is 25%. The more coins that are introduced into the system, the harder it is to randomly toss all of the coins in the air and have them all come up as heads. The more coins there are, the more disordered states there are compared to highly ordered states. If there are ten coins, for example, there are 1024 different states, but only one corresponds to all heads, and only one corresponds to all tails. More likely, there will be roughly equal numbers of heads and tails: disorder.

Most systems are much more complicated and have many, many more states than a coin. The video below shows a demonstration of different states of a beaker filled with colored cubes (purple and green). Before recording the video, Dr. Pasquale took all of the cubes out of the jar, manually sorted them, and put all of the green cubes on the bottom and all of the purple cubes on top (Figure 18.6, left). This is a highly ordered state of the system.

When Dr. Pasquale shakes the beaker, the cubes become arranged in a random manner and go into one of the many possible disordered states (Figure 18.6, right). Theoretically, it’s possible that she could continue to shake this jar for a very long time and get back to the highly ordered arrangement of green on bottom and purple on top. But it’s extremely unlikely due to the huge number of possible states. It is easy to increase the entropy of the system, but in order to decrease the entropy, Dr. Pasquale has to manually work to organize the cubes.

Two photographs of a beaker filled in with a few dozen purple and green cubes. On the left, the cubes have been sorted so that the green cubes are below the purple cubes. On the right, the beaker has been shaken and the cubes are in a random arrangement.
Figure 18.6 – A beaker filled with cubes has been manually arranged into a highly ordered state with all of the cubes sorted by color (left). After shaking the beaker, the cubes are in a highly disordered state (right). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

In the video below, Dr. Pasquale has a beaker of water and a container of blue food dye. There are many molecules of water in the beaker. When she places a few drops of food dye into the beaker, the two different substances, water and dye, are still relatively ordered. Most of the dye is in one location, and the water is still clear. Over time, however, the dye distributes throughout the water and the entropy increases. When Dr. Pasquale stirs the water, the dye distributes completely.

How would it be possible to get the water to become clear again (in other words, how could the entropy of the system be decreased)? How can the dye be separated from the water? This will not happen naturally. No amount of stirring or random motion will separate the blue food dye from the water. To decrease the entropy of the beaker of water, it would be necessary to distill the water or filter it out, manually putting energy and effort into the process.

One thing that the second law of thermodynamics tells us is that entropy increases with time. We saw that with the shaken cubes, and the food dye in the water. If you put effort into decreasing entropy somewhere, for example, by organizing the cubes, you yourself create heat from your exertions and increase the entropy of your surrounding environment. A refrigerator, which acts to decrease the entropy inside the fridge and cool down food, creates heat and actually causes an increase in entropy elsewhere. This is one of the reasons why perpetual motion is impossible. There is no way to decrease entropy in one spot without increasing it more somewhere else. We truly cannot get something for nothing!

By now, you should begin to see why a system left alone tends towards increasing disorder: with any given state being equally as probable as any other state, there are more ways to have disorder than there are to have order. Consider your surrounding environment. Think about how many molecules of air surround you, and how many different states they can be in. Most systems in our lives have many states they can take, and the highly ordered states only represent a very miniscule fraction of those possible states. Entropy is all around us.

We can consider entropy to describe the arrow of time. Some processes in physics are symmetric. That is, you could play a video of Dr. Pasquale walking around a room, and you would not necessarily be able to tell if the video was being played in forward or reverse. Dr. Pasquale can walk backward just as easily as she can walk forward. However, if you were to watch the video below, you would know that it is played backward. Why? Because you know that it is impossible to shake a can and obtain a more ordered state! Entropy describes the arrow of time. While it is possible to decrease entropy in some part of the universe, doing so will increase the entropy in another part of the universe by an amount that is greater than the decrease. Entropy of the universe always increases with time.

Further reading

  • Fire syringe explanation – This website goes into a “deep dive” of the physics behind the fire syringe. The mathematics used is outside the scope of this textbook, but as an overview the website gives a lot of information into this particular demo and adiabatic processes.

Practice questions

Conceptual comprehension

  1. Why do you think the Celsius scale isn’t used to calculate Carnot efficiency?

Numerical analysis

  1. A gas in a piston-cylinder system absorbs 200 J of heat while doing 150 J of work on the surroundings. Calculate the change in internal energy of the gas.
  2. A chemical reaction releases 5000 J of energy as heat while doing 3000 J of work on the surroundings. Calculate the change in internal energy of the system.
  3. A closed container of gas has an initial internal energy of 4000 J. Heat is added to the gas, increasing its internal energy to 6000 J while the gas does 2000 J of work on the surroundings. Calculate how much heat was added to the gas.
  4. A heat engine operates between two reservoirs at temperatures of 500 oC and 100 oC. Calculate the Carnot efficiency of this engine.
  5. A steam engine has a hot reservoir at 300 oC and a cold reservoir at 30 oC. Calculate the Carnot efficiency of this engine.
  6. A heat pump is used to heat a building. It extracts heat from the outside air at -10 oC and delivers it to the inside at 40 oC. Calculate the Carnot efficiency of this heat pump.
  7. A hypothetical engine operates between two reservoirs at temperatures of 800 K and 300 K. Calculate the Carnot efficiency of this engine.
  8. A single coin has two states, heads and tails. Consider a system consisting of four coins. Calculate…
    1. …the number of states of that system.
    2. …the percentage of highly ordered states (consisting of all heads or all tails) in that system.
  9. A single die has six states, corresponding to each face of the cube. Consider a system consisting of two dice. Calculate…
    1. …the number of states of that system.
    2. …the percentage of highly ordered states (consisting of both dice showing the same number) in that system.
  10. Consider a system consisting of three dice. Calculate…
    1. …the number of states of that system.
    2. …the percentage of highly ordered states (consisting of all three dice showing the same number) in that system.

Hands-on experiments

  1. Take two different liquids with distinct colors, such as water and colored water or milk, and gently pour them into a clear container. Initially, the two liquids will have a clear interface, but over time, they will mix and become one uniform color. Discuss how this demonstrates the increase in entropy as the liquids mix and achieve a more disordered state.
definition

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book