7. Work and energy

Summary

Work and energy are important concepts that allow us to understand and quantify the ability of objects to do something useful. That utility might be moving a piston in an engine, turning a wheel about an axis, or spinning a turbine to generate electricity. Work and energy are so intimately related that they have somewhat circular definitions that describe how intertwined they are. Energy is defined as the capability of an object to do work. And work is defined as the transfer of energy by applying a force to that object over a distance.

Work and energy as concepts can allow us to understand simple machines such as pulleys and levers, and also enable us to analyze the motion of projectiles, planets, and roller coasters, among other things.

Forms of energy

Energy is defined as the capability of an object to do work. The symbol used for energy depends on the type of energy being quantified, but regardless of the type of energy, the unit used for energy is the joule (J). A joule is a unit that contains other units hidden inside of it.

    \begin{align*} 1~\textrm{J} &= (1~\textrm{N})(1~\textrm{m})\\ &=(1~\textrm{kgm/s}^2)(1~\textrm{m})\\ &= 1~\textrm{kgm}^2/\textrm{s}^2 \end{align*}

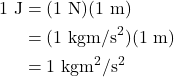
All three of these units mean the same thing: J, Nm, and kgm2/s2. However, the unit of Nm is typically not used when discussing work and energy, as it’s used as the unit for something called torque (which will be discussed in the next chapter of this textbook). Therefore, we will primarily use J as the unit for work and energy.

Energy and work are scalar quantities. That means that there is no direction associated with either of the two concepts, only a magnitude or strength.

There are many different forms of energy. In general, energy can be “kinetic,” which is energy due to motion. Energy can be “potential,” or stored energy, which is energy that exists based on the arrangement or configuration of something. For each form of energy, we have discovered a formula and have assigned a symbol to quantify that particular form of energy.

Kinetic energy

Kinetic energy is energy that objects have by virtue of their motion. Kinetic energy has a symbol of KE, units of J (joules), and an equation of

    $$KE = \frac{1}{2}mv^2,$$

where m is the mass of the object and v is the velocity of the object.

Remember that kinetic energy, like all forms of energy, is a scalar quantity. This is an important concept. Energy has no direction associated with it. When calculating kinetic energy, be very careful to use parentheses in your calculator when squaring the velocity. When taking the square of any number, positive or negative, the result will be positive. However, calculators are not so smart and may give you a negative answer if you do calculations without parentheses. It’s not possible to have negative kinetic energy. It would imply that it is possible to have less energy of motion than an object that isn’t moving, which doesn’t make sense at all!

Gravitational potential energy

Gravitational potential energy is stored energy that comes about due to the gravitational attraction between the Earth and other objects of mass. Gravitational potential energy has a symbol of GPE. (As previously mentioned, the unit for all types of energy is J.)

Consider where GPE comes from. An object sitting on a table has gravitational potential energy. If you push the object off the table, it will move downward, gaining kinetic energy. What aspects of the object sitting on the table can be changed to maximize GPE?

You can increase the gravitational potential energy by increasing the mass of the object. If you double the mass of the object, it will have twice the GPE. Tripling the mass gives three times the GPE. Therefore, GPE is directly proportional to mass.

You can also increase the GPE by raising the height of the table. The greater the height above our reference, the larger the GPE. Twice the height doubles the GPE and tripling the height triples the GPE. Therefore, GPE is directly proportional to height. For heights that are below the reference level, the GPE is negative. (Exactly what the height is measured in relation to – sea level, ground level, floor level, or something else – is up to you to decide. You just need to be consistent with that choice throughout the analysis.)

Finally, you can increase gravitational potential energy if you can somehow move the object of mass to a planet with a larger gravitational acceleration. The object would have more GPE on a planet like Jupiter or Saturn, and less GPE on a planet like Mars.

Tying this all together, we can look at the equation for gravitational potential energy

    $$GPE = mgh,$$

where m is the mass of the object, g is the magnitude of the gravitational acceleration, and h is the height above the reference level.

Elastic potential energy

Elastic potential energy is stored in the configuration of some type of deformable object. We can see this in a spring. The following video shows a mass bouncing up and down on a spring. When the mass is pulled downward, the deformation of the spring causes it to start moving once Dr. Pasquale lets go of the mass. The up and down motion, known as an oscillation, shows us the conversion of energy from elastic potential energy, to kinetic energy, to gravitational potential energy, over and over again as the mass bounces up and down.

Electrical energy

Electric potential energy comes from placing charged particles some distance apart from each other. This is the type of energy that can be stored in components used in electric circuits. If you have ever used a battery, or powered an electronic device using a wall outlet, then you have used electrical energy.

Chemical energy

Chemical energy is a type of stored energy that’s based on the configuration of atoms or molecules. For example, gasoline contains stored energy that we can use when we ignite it. Chemical energy is also how we as humans obtain energy from the food we eat during the digestive process.

Nuclear energy

Nuclear energy is the energy stored in the nucleus of an atom. This energy can be released in radioactive decay, fission, or fusion.

Radiant energy

Radiant energy is potential energy that’s stored in electromagnetic waves. There are many different categories of electromagnetic waves, each with a particular range of values for their energies. Visible light is the most common type of electromagnetic wave that we experience.

Heat (thermal) energy

Heat, or thermal energy, is energy that moves between objects that have different temperatures. The so-called “useful” types of energy are generally potential energy and kinetic energy. Heat can be utilized to do useful work, but is also where a lot of useful energy is wasted and cannot be used again. For example, when two objects rub together, the force of friction generates heat. We consider that heat to be wasted energy, as it cannot be utilized as useful work. The discussion of thermal energy and its transformations into other forms will be discussed later in this textbook.

Conservation of energy

Energy can be converted from one form to another. However, it cannot be created or destroyed. If we could somehow measure all of the energy in the entire universe today, and then measure it again tomorrow, those two numbers should be the same. This principle doesn’t just apply to the entire universe – it applies to any isolated system (a system in which no energy enters or leaves). Generators, motors, and engines are examples of devices that perform energy conversions. If you start making observations, you’ll probably notice energy conversions taking place all around you.

For example, an apartment or house in Illinois likely contains a gas furnace, which converts chemical energy to thermal energy. A microwave oven converts electrical energy to radiant energy (microwaves are a form of electromagnetic radiation). A coffee bean grinder converts electrical energy to kinetic energy. An electric stove converts electrical energy to thermal energy. (Many appliances in homes have an input form of electrical energy, as it is generally inexpensive and extremely convenient.) The table below lists some other common objects that convert energy from one form to another.

object

input energy

output energy

car (internal combustion engine)

chemical

kinetic

generator

electrical

kinetic

light bulb

electrical

radiant

the Sun

nuclear

radiant

human

chemical

kinetic, thermal

computer, smartphone

electrical

radiant, thermal, acoustic

plants

radiant

chemical

wind generator

kinetic

electrical

solar panel

radiant

electrical

In a rocket launch (such as that shown in Figure 7.1), chemical energy is converted to heat, sound, kinetic energy, and gravitational potential energy. Pretty impressive!

A 363 foot tall, 6,400,000 pound Saturn V rocket launches from Kennedy Space Center, Florida. It is propelled upwards into a clear blue sky by a jet of flames shooting out of the bottom boosters of the launch vehicle, creating clouds of smoke. The launch tower is a red steel framework.
Figure 7.1 – In a rocket launch, chemical energy is converted to kinetic energy, thermal energy, and acoustic energy. Saturn Apollo Program, by NASA Marshall Space Flight Center, is licensed under Public Domain.

A rather smashing demonstration of conservation of energy comes from the bed of nails. Demonstrated in the video below, Dr. Pasquale is lying in between two large pieces of wood that are studded with nails. Each nail is individually very sharp. The reason the nails don’t hurt (too much) is because there are enough nails to distribute her weight over a relatively large area. A cinder block is then placed over the upper piece of wood, and Dr. Fazzini swings a sledgehammer to break the brick. Dr. Fazzini raises the sledgehammer high above his head, giving it gravitational potential energy. As it swings downward, it gains kinetic energy. That kinetic energy is transferred to the cinder block and causes the block to break apart into many pieces. That is, energy from motion goes into separating some of the molecules in the block. Some of the energy goes to heat, and some of it goes to sound. The force from the blow is distributed along the upper layer of nails, which doesn’t cause too much discomfort due to the large number of nails. (Disclaimer: do not try this experiment at home!)

Energy in collisions

As we learned in the chapter on momentum, collisions between objects can be defined as inelastic or elastic. These two types of collisions can be distinguished by how kinetic energy is affected during the collision. While momentum is always conserved in a system in the absence of external forces, kinetic energy is not necessarily conserved in all collisions.

Kinetic energy in inelastic collisions

In an inelastic collision, kinetic energy is not conserved in the collision. This is because some of the kinetic energy of the system is lost to deformation or heat. In a perfectly inelastic collision, the maximum amount of kinetic energy is lost. In such collisions, the colliding objects literally stick together.

Traffic collisions are also examples of inelastic collisions. Consider two cars that collide on the road. A red car with a mass of 1400 kg traveling at an initial velocity of 9 m/s collides with a blue car with a mass of 1100 kg traveling at an initial velocity of -18 m/s. After the collision, the red car travels at a velocity of -5.3 m/s and the blue car travels at a velocity of 0.2 m/s. (None of the occupants of the vehicles are harmed in this hypothetical example.)

The initial kinetic energy of the system is

    \begin{align*} KE_i &= \frac{1}{2}m_{red}v_{i, red}^2 + \frac{1}{2}m_{blue}v_{i, blue}^2\\ &= \frac{1}{2}(1400~\textrm{kg})(9~\textrm{m/s})^2 + \frac{1}{2}(1100~\textrm{kg})(-18~\textrm{m/s})^2\\ &= 56700~\textrm{J} + 178200~\textrm{J}\\ &= 234900~\textrm{J}. \end{align*}

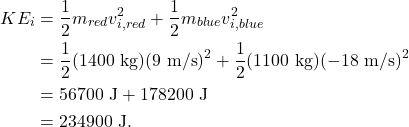
After the collision, the kinetic energy of the system is

    \begin{align*} KE_f &= \frac{1}{2}m_{red}v_{f, red}^2 + \frac{1}{2}m_{blue}v_{f, blue}^2\\ &= \frac{1}{2}(1400~\textrm{kg})(-5.3~\textrm{m/s})^2 + \frac{1}{2}(1100~\textrm{kg})(0.2~\textrm{m/s})^2\\ &= 19663~\textrm{J} + 22~\textrm{J}\\ &= 19685~\textrm{J}. \end{align*}

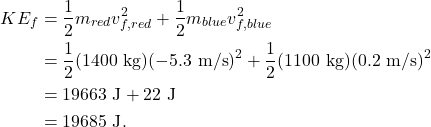
Kinetic energy is not conserved in this collision. Some (215215 J) of the energy of motion was converted to sound, heat, and other forms of energy.

Kinetic energy in elastic collisions

In an elastic collision, kinetic energy is conserved in the collision. We can anticipate that a collision will be elastic if the two objects colliding won’t create any heat from rubbing together, if they won’t create any sound, and if the molecules inside the objects won’t permanently deform when they impact together.

Once again, consider the red and blue cars (in which none of the occupants are harmed in a collision). If the two cars have the uncanny ability to collide without physically impacting each other, no physical deformation, sound, or heat will be lost in this collision. After the collision, the red car travels at a velocity of -14.76 m/s and the blue car travels at a velocity of 12.24 m/s.

The initial kinetic energy of the system is still 234900 J. After the collision, the kinetic energy of the system is

    \begin{align*} KE_f &= \frac{1}{2}m_{red}v_{f, red}^2 + \frac{1}{2}m_{blue}v_{f, blue}^2\\ &= \frac{1}{2}(1400~\textrm{kg})(-14.76~\textrm{m/s})^2 + \frac{1}{2}(1100~\textrm{kg})(12.24~\textrm{m/s})^2\\ &= 152500.32~\textrm{J} + 82399.68~\textrm{J}\\ &= 234900~\textrm{J}. \end{align*}

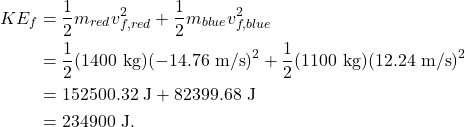
Mechanical energy

Mechanical energy (ME) is equal to the sum of the potential energy and kinetic energy of an object. In other words,

    $$ME = PE + KE.$$

In the absence of dissipative effects such as friction and drag, the mechanical energy will be conserved in a system. Conservation of mechanical energy can therefore be a very useful way to calculate properties of an object.

In the video below, a set of tracks is used to demonstrate conservation of mechanical energy. The tracks all have equal starting heights, and equal ending heights. That means that all of the GPE that the balls have at the start will be converted to equal amounts of KE at the end. Because each of the balls is identical, they will have the same velocity when they reach the end of the track. How far the ball goes as it launches off the end of the track is related to the velocity. When the balls are released from the tracks, while they might take different amounts of time to reach the end, they all hit the ground the same distance away, indicating that they all had the same amount of mechanical energy throughout their motion.

The amount of time it takes for the balls to reach the end of the tracks has to do with the average speed of each of the balls. If you go fast for a longer period of time, then you’ll reach the end first. This is why the ball moving down the ramp with the earliest down-slope (the blue ramp in the video) reaches the end of the track the fastest. But regardless, the conservation of mechanical energy still holds up.

A roller coaster (an example of which is shown in Figure 7.2) provides a great example of conservation of mechanical energy. A chain driven by chemical or electrical energy will convey a cart to the top of the first hill. If there are no more chains to provide any other input energy, then the first hill must be the tallest part of the roller coaster. At the top of that hill, the cart has all GPE and no KE. As it moves downward, the GPE converts to KE. At the lowest point in the track, the KE of the coaster, and therefore its speed, is at its highest value. As long as the level of the track remains lower than the starting hill, the energy the roller coaster has at the start will keep it moving throughout the ride (assuming there is no friction).

Photograph of a roller coaster with blue steel framework and a yellow track. The roller coaster rises up much taller than the surrounding trees, and in the background can be viewed a gray sky.
Figure 7.2 – A roller coaster’s initial hill must be tall enough to provide sufficient energy for the car to make it to the end of the track (unless there are other forms of input energy later in the ride). Nitro coaster, by Dusso Janladde, is licensed under CC BY-SA 3.0.

If the roller coaster were designed with a taller hill after the start, there would not be enough energy to get the roller coaster up that hill. In an actual ride, there would need to be a drive chain that provides that energy from chemical or electrical sources to get the cart up to the top of that next tall hill.

Solving kinematics equations using conservation of mechanical energy

When solving for properties of an object in free fall (ignoring forces such as friction and air drag), the conservation of mechanical energy can be used instead of using the equations of accelerated motion introduced earlier in this textbook.

Say a 0.1 kg apple is dropped from a height of 400 m, and that apple does not experience any air drag or friction as it falls through the atmosphere to the ground. There is no wind, and the apple has no horizontal velocity at any point in time throughout its journey. The initial form of energy of the apple is entirely GPE, as there is initially no motion. The GPE (and total ME) of the apple is

    \begin{align*} GPE &= (0.1~\textrm{kg})(9.8~\textrm{m/s}^2)(400~\textrm{m})\\ &= 392~\textrm{J}. \end{align*}

How fast will the apple be moving at the instant before it hits the ground? At that point, the height of the apple will be 0 m, and its mechanical energy will be entirely in the form of KE (GPE = 0 J). We can set the KE equal to 392 J and solve for the speed, which is

    \begin{align*} v &= \sqrt{\frac{2KE}{m}}\\ &= \sqrt{\frac{2(392~\textrm{J})}{0.1~\textrm{kg}}}\\ &= \sqrt{7840~\textrm{m}^2/\textrm{s}^2}\\ &= 88.5~\textrm{m/s}. \end{align*}

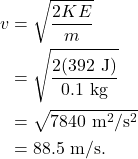
The table below shows the values of GPE and KE at different points in the journey of the apple. The values of KE at any height can then be used to solve for the instantaneous speed of the apple.

h (m)

ME (J)

GPE (J)

% GPE

KE (J)

% KE

400

392

392

100

0

0

300

392

294

75

98

25

200

392

196

50

196

50

100

392

98

25

294

75

0

392

0

0

392

100

Alternatively, if we know the velocity of the apple at any point in its journey, we can use conservation of mechanical energy to solve for its height at that moment in time. Say the apple is known to have a speed of 20 m/s. What is the height? The value of KE can be calculated as

    \begin{align*} KE &= \frac{1}{2}(0.1~\textrm{kg})(20~\textrm{m/s})^2\\ &= 20~\textrm{J}. \end{align*}

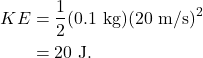
Because the total mechanical energy of the apple is 392 J, if 20 J is in the form of KE, the remaining 372 J must be in the form of GPE. Set the value of GPE equal to 372 J and solve for the height, and we find that

    \begin{align*} h &= \frac{GPE}{mg}\\ &= \frac{372~\textrm{J}}{(0.1~\textrm{kg})(9.8~\textrm{m/s}^2)}\\ &= 379.6~\textrm{m} \end{align*}

Systems with dissipative forces

The video below demonstrates a good example of a system that contains some dissipative forces like air drag and friction. Dr. Pasquale stands against a wall, holding a pendulum right up against her nose. The pendulum is not moving, so all of its mechanical energy is in the form of GPE. She then releases the pendulum by letting it fall, and the large mass swings away from her, gaining KE as it gets to the bottom of its motion. It gains GPE again on the upswing, and this conversion occurs in reverse as it swings back to her face.

By the time the heavy mass reaches Dr. Pasquale’s face again, the ball has lost some of its mechanical energy, which means that it is no longer able to get to the same height. This means that as long as she doesn’t move her face away from the wall, she can be very confident that the ball will not hit her in the face when it returns. The heavy mass experiences air drag as it travels through the air, and the pin holding it to the ceiling experiences friction as it rubs against the ceiling supports.

In much the same way, a roller coaster, which we discussed earlier, must start out with a sufficient amount of mechanical energy to give the ride enough energy to continue throughout its entire motion without any more input work. If there’s only one drive chain bringing the roller coaster cart up to the top of the tallest hill, that GPE must be enough to not only get the roller coaster to the end of the track, but also be able to account for the energy converted to sound and heat due to friction and air drag.

Work

We need to be careful when discussing the concept of work in a physics context. You may use the word work to talk about something you do to make money. Or maybe you think about going to the gym or otherwise physically exerting yourself. Be careful! Work, when we’re using it to refer to a physics phenomenon, has a very specific meaning that cannot be interchanged with our loose definition of “work” that we use in everyday language.

Work is energy that is transferred to an object by exerting a force on that object through a distance. Work has a symbol of the uppercase letter W. The units are joules (J). The equation for work is

    $$W = F_{//}d,$$

where d is the displacement of the object and F_{//} is the component of force that is parallel to the displacement of the object (the // symbol denotes the concept of “parallel”). In order to calculate the work done by the force, it is important to only use the component of the force that is parallel to the displacement.

While work is a scalar quantity, indicating that it has no direction associated with it, it is still possible to do positive or negative work. Positive work means that the parallel force points in the same direction as the displacement, and negative work means that the parallel force points in the opposite direction as the displacement. In this manner, we can discuss the concept of net work, which considers the effect of both applied forces and any dissipative forces (such as friction and air drag) that act on an object.

When a force acts on an object, Newton’s second law states that the object will experience an acceleration (which could cause the object to speed up, slow down, or change direction). It’s possible that the displacement, or motion of the object, and the force may not be pointed along exactly the same line. A great example of this is the motion of a wheeled suitcase, depicted in Figure 7.3.

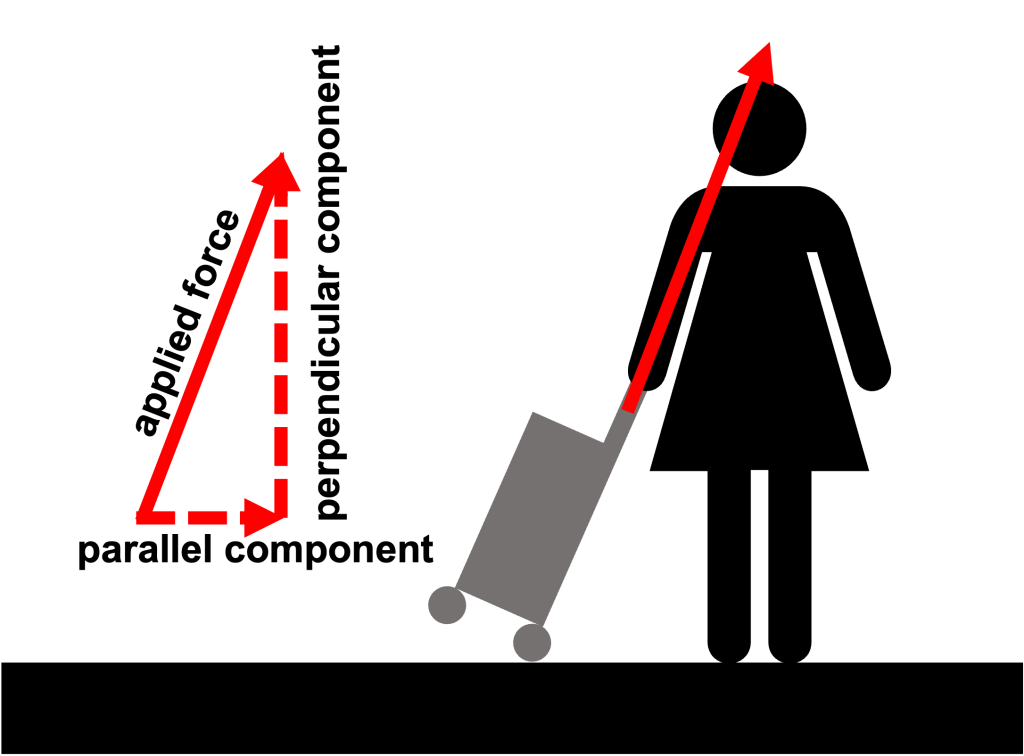
Image of a stick figure holding a suitcase with the handle at an angle. A red arrow points along the direction of the applied force, parallel to the handle of the suitcase. On the left-hand side of the image is a breakdown of that red arrow into parallel and perpendicular components of force.
Figure 7.3 – A person applies a force to a wheeled suitcase to pull it along the floor (right). The parallel and perpendicular components of the applied force are shown (left). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

A wheeled suitcase can be rolled along a floor, which is much easier than older styles of luggage that you had to carry. This way, most of the weight of the suitcase can be supported by the floor. The wheels allow the force we apply to the handle to cause the suitcase to move in the same direction as our body. We apply the force on the handle at an angle, but the suitcase does not move along the same line as our force.

The traveler pulls the suitcase in Figure 7.3 horizontally to the right. The horizontal distance that the suitcase moves is the displacement. The applied force (shown on the left of Figure 7.3) is broken down into components: a component that’s parallel to the displacement, and a component that’s perpendicular to the displacement.

Only the parallel component of force is doing work. And the work is equal to the parallel component of force multiplied by the displacement of the suitcase. The perpendicular component of the force is keeping the suitcase upright, but it isn’t doing any actual work, from a physics perspective.

Say the traveler in Figure 7.3 applies 113 N of parallel force on the suitcase, with a horizontal component of 15 N and vertical component of 112 N. The traveler pulls the suitcase horizontally along the ground a distance of 2 m. The work done on the suitcase by the traveler is

    \begin{align*} W &= (15~\textrm{N})(2~\textrm{m})\\ &= 30~\textrm{J}. \end{align*}

This work is positive: the parallel component of the force and the displacement of the object both point in the same direction.

Suppose there’s 8 N of friction opposing the motion of the suitcase. The work done by friction is

    \begin{align*} W &= (-8~\textrm{N})(2~\textrm{m})\\ &= -16~\textrm{J}. \end{align*}

Friction does -16 J of work (negative, because force and displacement oppose each other). The net work that is done on the suitcase is

    \begin{align*} W_{net} &= 30~\textrm{J} - 16~\textrm{J}\\ &= 14~\textrm{J}. \end{align*}

What if a force is applied perpendicular to the motion of an object? Consider holding a heavy bowling ball at a constant height as you walk at a constant speed from one side of a room to another. The displacement vector will be a horizontal line in the direction of your motion. The force that you apply to the bowling ball, however, points up. The force and the displacement are perpendicular. While it may be hard for you to carry the bowling ball, and you will likely feel like you’re exerting yourself, from a physics perspective, you are doing zero work on the bowling ball!

Work-energy theorem

As just described, when a force is applied on an object parallel to its displacement, work is done on that object. Newton’s second law tells us that force equals mass times acceleration, implying that the object will speed up, slow down, or change direction. If the work done on the object is positive, it will speed up, gaining kinetic energy. If the work done on the object is negative, it will slow down, losing kinetic energy.

By how much? The work-energy theorem can be used to quantify this. The work-energy theorem states that work is equal to the change in kinetic energy of an object.

    \begin{align*} W &= \Delta KE\\ &= KE_{final} - KE_{initial} \end{align*}

If 10 J of positive work is done on an object, then the kinetic energy of that object will increase by 10 J.

Consider the traveler from Figure 7.3 who does 30 J of work on a suitcase having a mass of 50 kg (in this case, there is no friction). If the suitcase starts at rest (which corresponds to an initial KE of 0 J), we can use the work-energy theorem to calculate the final kinetic energy of the suitcase: 30 J. The final velocity of the suitcase is therefore

    \begin{align*} v_{final} &= \sqrt{\frac{2(30~\textrm{J})}{50~\textrm{kg})}}\\ &= \sqrt{1.2~\textrm{m}^2/\textrm{s}^2}\\ &= 1.1~\textrm{m/s}. \end{align*}

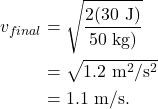
Power

Mechanical work is useful to us, especially when harnessed in a device such as a motor. Mechanical work is done in the engine of a car to move us around from one place to another. But work by itself isn’t always enough information. How do we describe the engine of a car? Usually we talk about how much horsepower it has. What is horsepower, and what does it measure?

Horsepower is one unit that’s used to quantify the concept of power. While we will not use horsepower in this class, it is used frequently in the United States. It was originally used to relate the capability of motors to horses.

In short, power quantifies how quickly work is done. Power has a symbol of the uppercase letter P. We will use the SI unit watt (W), which is equal to joules per second (J/s). The equation for power is

    $$P = \frac{W}{t},$$

where W is the work done by the person, object, or machine, and t is the amount of time it takes to do that work.

A golf cart and a sports car will both be able to move us from point a to point b. But a golf cart will speed up much more slowly than the sports car. The golf cart is therefore less powerful.

Consider a 500 kg golf cart that speeds up from rest to 9 m/s in the time span of 60 s. We can use the work-energy theorem to calculate the work done by the motor, and then divide by time to calculate the power. The work is equal to the change in kinetic energy. Because the golf cart was initially at rest, the initial KE is zero. The final KE (and work) is therefore

    \begin{align*} W &= \frac{1}{2}(500~\textrm{kg})(9~\textrm{m/s})^2\\ &= 20250~\textrm{J}. \end{align*}

To calculate power, divide by time. The power of this golf cart is

    \begin{align*} P &= \frac{20250~\textrm{J}}{60~\textrm{s}}\\ &= 337.5~\textrm{W}. \end{align*}

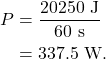
For context, if you are familiar with the unit of horsepower, 337.5 W corresponds to approximately 0.5 hp. (The conversion is 1 hp = 746 W.)

Compare that golf cart to a sports car with a mass of 1600 kg that speeds up from rest to 27 m/s in 3 s. First, solve for work using the work-energy theorem. We find that work is equal to

    \begin{align*} W &= \frac{1}{2}(1600~\textrm{kg})(27~\textrm{m/s})^2\\ &= 583200~\textrm{J}. \end{align*}

The power of the sports car is

    \begin{align*} P &= \frac{583200~\textrm{J}}{3~\textrm{s}}\\ &= 194400~\textrm{W}. \end{align*}

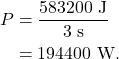
This sports car has a power rating of 194400 W (260 hp). In case we needed mathematical evidence, a sports car is much more powerful than a golf cart!

Simple machines

A simple machine is used to change either the direction or magnitude (or both) of an applied force. There are essentially six types of simple machines: levers, wheels and axles, pulleys, inclined planes, wedges, and screws. (Some would argue that there are really only four types by stating that the wedge is just two inclined planes placed back-to-back, and that the screw is an inclined plane wrapped around an axle.)

Some simple machines can multiply an input force. This force multiplication is called mechanical advantage. Mechanical advantage has a symbol of MA. The equation for mechanical advantage is

    $$MA = \frac{F_{out}}{F_{in}},$$

where F_{out} is the force output generated by the machine (say, the weight of the heavy object that the machine is lifting) and where F_{in} is the force input by the user of the machine. Because in this equation, one force is divided by another, mechanical advantage is a unitless quantity.

What is the tradeoff that we have to deal with when using a simple machine? Hopefully your understanding of physics at this point makes you feel profoundly uncomfortable with the idea that something could come out of nothing. In fact, while force can be multiplied, the work put into the simple machine will be equal to the work output of the simple machine (ideally). Because work is equal to force times distance, the operator of the simple machine will apply less force than the machine will output, at the cost of applying that force over a longer distance than the output of the machine will generate.

Efficiency quantifies how well work input is converted to work output. The symbol for efficiency is the lowercase letter e. The equation for efficiency is

    $$e = \frac{W_{out}}{W_{in}},$$

where W_{out} is the output of the machine, and W_{in} is the input to the machine. Efficiency is unitless, but we usually multiply the result by 100 to express it as a percentage. In ideal situations, efficiency will be 100%. However, in reality, friction, air drag, or other situations such as bending of a simple machine will cause the efficiency of a simple machine to be less than 100%.

Lever

Perhaps you’ve heard the Archimedes quote, “Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.” While literally moving the world would be impractical, not to mention inconvenient, levers can be used to lift a heavy object using less force than we get out of the system. A seesaw, which is an example of a lever, is shown in Figure 7.4.

A black and white photograph of two children playing on a seesaw at the Webster School playground, with one of the children hanging by her hands from the raised end. Her feet dangle about a meter above the ground. A few dozen other schoolchildren and teachers look on in the background.
Figure 7.4 – View of two children playing on a seesaw (lever) at a playground in Chicago, Illinois. A girl is hanging by her hands underneath the raised half of the seesaw, and a boy is holding down the lowered half of the seesaw. Two children playing on a seesaw at the Webster School playground by DN-0000074, Chicago Daily News collection, Chicago History Museum.

To use a lever to generate mechanical advantage requires a pivot that is not located in the center of the lever (as it is in Figure 7.4, where the mechanical advantage is equal to one). In this case, the mechanical advantage comes from lifting a large force over a short distance using a small force over a long distance, shown in Figure 7.5. The shorter the distance between the end of the lever containing the heavy object and the pivot, the larger the mechanical advantage, all other things being equal.

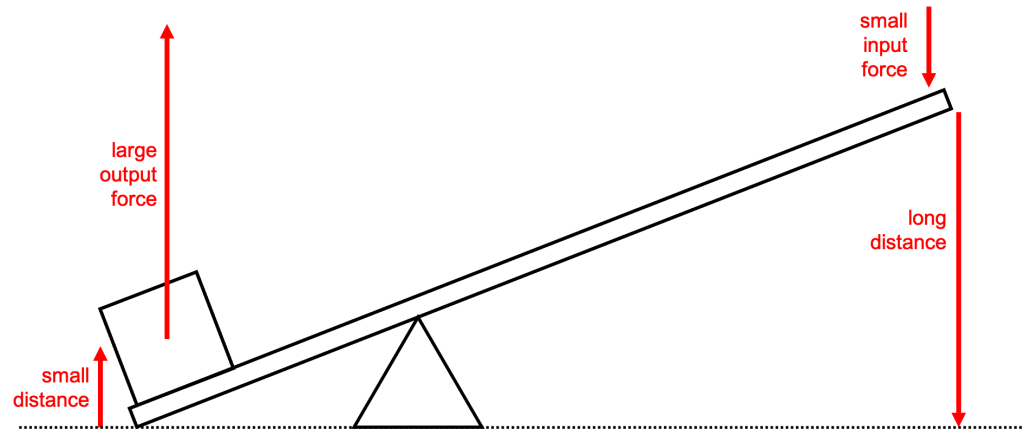
A diagram of a lever (long rectangle) on a pivot (triangle) that is placed left-of-center. A large weight (depicted by a square) can be lifted a short distance by using a small force exerted over a long distance.
Figure 7.5 – Mechanical advantage is generated with a lever by placing the pivot away from the center. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Since energy is conserved, you cannot get more work output than the work input. Under ideal conditions (no friction, deformation, or other dissipative effects), the work output would be equal to the work input:

    \begin{align*} W_{out} &= W_{in}\\ F_{out}D_{out} &= F_{in}D_{in}. \end{align*}

SInce there will always be some friction at the pivot and some bending of the lever, not all of the input work goes into lifting the load. Friction at the pivot dissipates some of the input work into thermal energy and the bending of the lever stores some of the input work as elastic potential energy. Thus, the work that actually goes into lifting the load is slightly less than the work input (W_{out} < W_{in}):

    $$W_{out} + \textrm{Elastic Potential Energy Stored} + \textrm{Thermal Energy Dissipated} = W_{in}.$$

Wheel and axle

A wheel and axle is also a simple machine. A linear force can be used to cause rotation, and the force can be multiplied if the wheel and axle system is set up to have a mechanical advantage. Wheelchairs, bicycles (Figure 7.6), and cars are all examples of objects that use the wheel and axle simple machine.

A black bicycle is propped upright by means of a kickstand on a concrete walkway.
Figure 7.6 – A bicycle is an example of a technology that uses the wheel and axle simple machine. Triumph Cycle bicycle, by Andrew Dressel, is licensed under CC BY-SA 3.0.

Pulley

Pulleys are capable of changing the direction of a force. They can also multiply a force. The mechanical advantage of a pulley system is related to the number of sections of the string (or rope) used in the pulley system that support the load.

A single fixed pulley (Figure 7.7, Scenario A) doesn’t create any mechanical advantage, but allows us to pull down on an object to lift it, rather than pulling up, which may be more difficult for us to do, especially if we have bad knees or a bad back! However, a single pulley that connects to the load and is connected with two sections of string (Figure 7.7, Scenario B) will have a mechanical advantage of two.

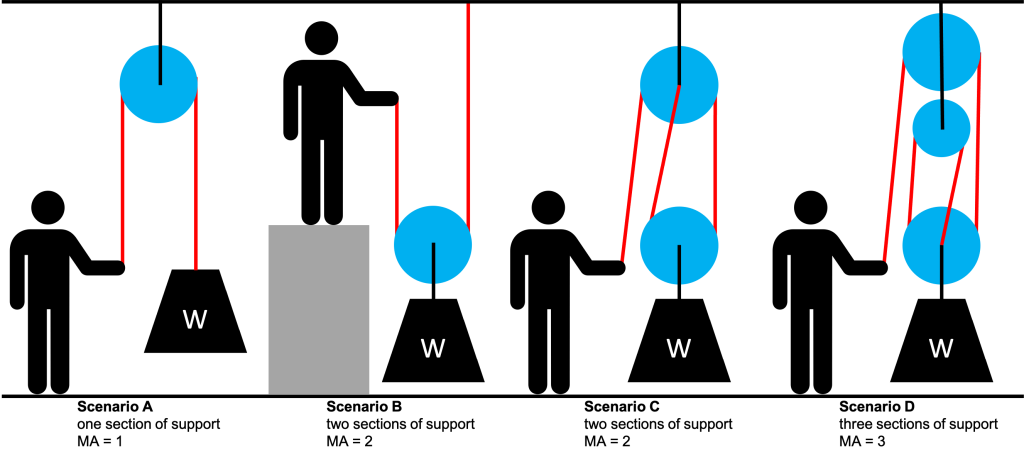
Diagram of four scenarios of mechanical advantage in pulleys. Scenario A shows a stick figure pulling down on a string connected to a fixed pulley, with one point of contact with the load (MA = 1). Scenario B shows a stick figure pulling up on a string connected to a moveable pulley, with two points of contact with the load (MA = 2). Scenario C shows a stick figure pulling down on a string connected to two pulleys, generating two points of contact with the load (MA = 2). Scenario D shows a stick figure pulling down on a string connected to three pulleys, generating three points of contact with the load (MA = 3).
Figure 7.7 – The mechanical advantage of a pulley is equal to the number of sections of string (or rope) directly supporting the load. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

The more sections of support there are in the system, the less input force we need to apply to lift an object. (Figure 7.7, Scenarios C and D.) However, the caveat is that we must apply the force over a longer distance. The concepts of mechanical advantage and efficiency still apply.

Pulleys are used in many different applications, including redirecting forces from a yoke or stick and rudder pedals on an airplane to flight controls (elevator, ailerons, rudder), cable machines at the gym, elevator cables, and hoists.

Inclined planes

Inclined planes are also known as ramps. You’ve probably seen them at building entrances, providing an accessible way to enter a building that would otherwise require steps (see Figure 7.8). Not only do ramps provide accessibility, but they also reduce the amount of force that’s required to move along the ramp. The mechanical advantage of the inclined plane is related to the steepness of the slope of the ramp. As mentioned, the lower the force, the longer the distance that the force must be applied in order to obtain the desired amount of work output. As a result, the smaller the force you wish to apply, the greater the length of the ramp is required. This should make sense since if the ramp has a shallower angle, the ramp will need to be longer in order to reach the desired height.

A wheelchair user is photographed from behind has they wheel up an outdoor brick ramp to access a building.
Figure 7.8 – A wheelchair user utilizes a ramp (inclined plane) to enter a building. Access to the ramp in a wheelchair, by Gov39.ru, is licensed under CC BY 4.0.

Wedge

A wedge is a simple machine found in things such as axes, knives, scissors, and wood splitters (see Figure 7.9). A force applied to the blunt edge of the wedge is transmitted to the pointy edge, which in turn redirects the force in a direction that is perpendicular to the “inclined” surfaces of the wedge. As such the wedge can be used to split something apart.

A photograph of a metal wedge.
Figure 7.9 – A wood splitting wedge. Wedge, by Shakespeare, is licensed under CC BY-SA 3.0.

Screw

A screw takes rotational motion and converts it to linear motion. You may have used screws or bolts (see Figure 7.10) when putting together furniture or building something. As stated earlier, a screw can be thought of as an inclined plane wrapped around an axle. Like a wedge, the force on the screw head is transmitted in a direction perpendicular to the “incline,” which then acts somewhat like a wedge to drive the screw into the object.

A photograph of a metal bolt (with nut screwed on) and a screw.
Figure 7.10 – A bolt (with a nut) and a screw. Bolt and screw, by Tomasz Sienicki, is licensed under CC BY 3.0.

Practice questions

Conceptual comprehension

  1. What is the conceptual issue with the cartoon shown in Figure 7.11? Should the person at the bottom of the ladder flinch?
A cartoon of a stick figure wearing a top hat standing at the top of a ladder holding the heavy weight of a pendulum. At the bottom of the ladder is a second stick figure. The figure wearing the top hat says "Okay, hold still. And remember, if you really believe in the laws of physics, you won't flinch."
Figure 7.11 – Is this cartoon conceptually sound? Should the person at the bottom of the ladder flinch? Laws of Physics, by Randall Munroe, is licensed under CC BY-NC 2.5.

Numerical analysis

  1. Calculate the gravitational potential energy of an object with a mass of 10 kg when it is positioned 5 m above the Earth’s surface.
  2. Calculate the gravitational potential energy of a 15 kg object that is situated 20 m above the Earth’s surface.
  3. Calculate the gravitational potential energy of a spaceship with a mass of 15,000 kg positioned 50 m above the surface of the Moon. (The Moon has an acceleration due to gravity of approximately 1.6 m/s2.)
  4. Calculate the kinetic energy of a 12 kg object when it is moving at a speed of 20 m/s.
  5. Calculate the kinetic energy of an object with a mass of 3.2 kg when it is traveling at a velocity of -8.5 m/s.
  6. A 2 kg object initially at rest is released from a height of 10 meters above the ground. Calculate its total mechanical energy at the starting point and when it’s 5 meters above the ground. Calculate the KE at both heights.
  7. A 500 g ball is dropped from a height of 15 meters. Determine its velocity just before it hits the ground.
  8. A 5 kg object is sliding down a frictionless hill with a height of 8 meters. Calculate its speed at the bottom of the hill.
  9. A 3 kg object is swinging back and forth on a pendulum. If its maximum height above the lowest point is 2 meters, calculate its velocity at the lowest point.
  10. A car engine exerts a force of 5,000 N to move a car a distance of 100 meters. Calculate the work done by the engine.
  11. A person pulls a sled with a force of 65 N (the force has a horizontal component of 33 N and a vertical component of 56 N), moving it a horizontal distance of 10 meters. Calculate the work done by the person.
  12. A perfectly efficient pulley system is used to lift a 100 kg weight to a height of 5 meters in 10 seconds. Calculate the power output of the pulley system.
  13. A ramp is used to lift a 500 kg object to a height of 4 meters in 20 seconds. Calculate the power applied to lift the object using the ramp. You may safely ignore forces such as friction and air drag.
  14. A person pushes down on a lever. The distance the person pushes down is 50 cm. The load is lifted upward a distance of 10 cm. Calculate the mechanical advantage of the lever.
  15. A person pulls a 100 N object up an inclined plane a length of 5 meters. The force the person exerts on the object is 80 N. Calculate…
    1. …the distance the object moved upward.
    2. …the mechanical advantage of the inclined plane.
  16. A pulley system consists of two pulleys. Calculate the mechanical advantage of the pulley system.
  17. A person uses a lever to lift an 80 N force a distance of 20 cm. The person exerts a force of 40 N over a distance of 50 cm to obtain this output. Calculate…
    1. …the mechanical advantage of the lever.
    2. …the work input to the simple machine.
    3. …the work output from the simple machine.
    4. …the efficiency of the lever.
  18. A pulley system requires an input force of 60 N exerted over 10 m to lift a load, but due to friction and other losses, the pulley system only does 480 J of useful work. Calculate…
    1. …the work input to the simple machine.
    2. …the efficiency of the pulley system.

Hands-on experiments

  1. Create a simple lever using a ruler or a wooden board and a small object as a load. Experiment with different positions for the fulcrum and observe how it affects the effort needed to lift the load. How does this relate to the mechanical advantage of the lever?
  2. If you have a wind-up toy, wind it up, release it, and measure how far it travels. Try different amounts of winding, and see how the results change. What does this experiment tell you about work, energy transfer, and efficiency? What external forces may be affecting the efficiency of this toy?
definition

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book