22. Electrostatics

Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; Carley Bennett, Ph.D.

22. Electrostatics

Summary

Electrostatics introduces an important new property of matter: electric charge. This property unlocks the concepts of electricity and magnetism, which we’ll be exploring in the next several chapters of this textbook. This discussion will explain what electric charges are and how they give rise to forces and electric fields.

Charge

Electrical charge is a fundamental property of matter that causes particles that carry a charge to experience a force when in the presence of an electric field. This is somewhat analogous to mass, which is a fundamental property of matter that causes objects of mass to experience a force when in the presence of a gravitational field. Just as mass is conserved, charge is also a conserved quantity. This means that the total charge in any closed system must remain constant over time. Charge can neither be created nor destroyed.

The term electrostatics, which is the topic of this chapter, has to do with charges that do not move. We will discuss all of the fascinating properties of charges that do move in the next chapter on electric circuits.

Charge has a symbol of the lowercase letter $q$ . (It’s possible you may see the uppercase letter $Q$ used for charge in other textbooks.) We use the unit coulomb, which has a symbol of the capital letter C.

There are two types of charges: positive charges and negative charges. Every proton carries a positive charge, and every electron carries a negative charge. The magnitude of the charge of an electron is equal to the magnitude of the charge of a proton. The value of this charge is known as the elementary charge, and has a symbol of the lowercase letter $e$ . The value of the elementary charge is

$e = 1.6 \times 10^{-19}~\textrm{C}.$

Each proton carries a positive charge of $+e$ , and each electron carries a negative charge of $-e$ . In a material or object that is neutral, the magnitude of positive charge is exactly equal to the magnitude of negative charge.

In addition to being conserved, charge is also quantized. This means that charge can only come in particular values which are integer multiples of the value $e$ . This is because there can only be whole numbers of protons and electrons. As it is not possible to have a fraction of an electron, or a fraction of a proton, the amount of charge that any object can have must come in integer values of the magnitude of the elementary charge. That is, $|q| = Ne$ , where $N$ is an integer.

There are two possible interactions that charges can experience. Two like charges (positive and positive, or negative and negative) will repel. That is, if you could somehow hold two like charges together, they would experience a force that causes them to move apart from each other. Two unlike charges (positive and negative) will attract. Therefore, if you could somehow hold two unlike charges apart from each other, they would experience a force that causes them to come together.

We can visualize the effect of this force by looking at how charges interact on a low-friction turntable. In the video below, two acrylic rods are rubbed with paper. This removes electrons, causing a positive charge in both rods. When one of the rods is free to rotate, and the other rod is held nearby, we can see that the first rod rotates away. Positive charges repel other positive changes.

In the video below, two PVC rods are rubbed with paper. This process adds electrons to the PVC, causing a negative charge. Holding one negatively charged PVC rod near the one on the turntable causes the PVC rod on the turntable to rotate away, demonstrating electrostatic repulsion. Negative charges repel other negative changes.

When the negatively charged PVC and positively charged acrylic are held nearby, now the positive rod rotates toward the negative rod, demonstrating a force of attraction between the unlike charges.

The above video demonstrations show how charged objects behave when held near other charged objects. What about when a charged object is held near a neutral object?

In the video below, Dr. Pasquale places one of the charged rods close to a neutral object (a wooden meter stick resting on a pivot). When the charged rod gets close to the meter stick, it experiences a torque, causing it to rotate. This demonstrates an attractive force with the charged rod. Both positively and negatively charged rods create an attractive force with neutral objects.

How is it possible to give objects positive or negative charge? We know that atoms have a positively charged nucleus comprised of protons and neutrons, and that electrons orbit the nucleus. It is very complicated to add or remove protons from an atom. It requires a nuclear process such as radioactive decay, fission, or fusion. Because electrons orbit the nucleus, it is much simpler to add or remove electrons than to add or remove protons. Therefore, to give an object a positive charge, we remove electrons and to give an object a negative charge, we add electrons.

An ion with a charge of negative two has that charge because it has two excess electrons. An ion with a charge of positive three has that charge because it has three fewer electrons than protons.

Coulomb’s law

If two like-charged particles are held near each other, they will move away from each other if let go. If they start at rest, then move away from each other, that means the two charges will speed up, indicating that an acceleration is present. From Newton’s second law, we know that when there’s acceleration, there’s a net force. Charged particles exert forces on each other.

Coulomb’s law is the equation that quantifies the force that exists between particles. The magnitude of this force is given by the equation

$|F| = k \frac{|q_1||q_2|}{d^2}.$

That is, the force equals a constant ( $k$ ) times the charge of one of the particles, times the charge of the second particle, divided by the distance between the two particles squared. The unit of force, as always, is the newton.

The constant $k$ is known as Coulomb’s constant and has a value of $9 \times 10^9~\textrm{Nm}^2/\textrm{C}^2$ .

Note the similarities with the equation for gravitational force! Both forces have a constant term, a multiplication of the two physical properties (mass for gravity, charge for electrostatic force), and are divided by the distance squared. This means that electrostatic force, just like gravity, obeys the inverse-square law. Halving the distance between two charges will quadruple the force between them, while doubling the distance will cut the force to a fourth of its original value.

Gravitational forces and electrostatic forces also have some significant differences. One of the biggest differences is that the electrostatic force is much stronger than gravity. To attempt to quantify this, we can calculate both the electrostatic force and gravitational force that exist between a single proton and single electron in a hydrogen atom. The ratio of electrostatic force to gravitational force can be calculated as

$\begin{align*} \frac{F_{electrostatic}}{F_{gravitational}} &= \frac{k|q_{proton}||q_{electron}|}{Gm_{proton}m_{electron}}\\ &= \frac{(9 \times 10^9~\textrm{Nm}^2/\textrm{C}^2)(|1.6 \times 10^{-19}~\textrm{C}|)(|-1.6 \times 10^{-19}~\textrm{C}|)}{(6.67 \times 10^{-11}~\textrm{Nm}^2/\textrm{kg}^2)(1.67 \times 10^{-27}~\textrm{kg})(9.11 \times 10^{-31}~\textrm{kg})}\\ &= \frac{2.3 \times 10^{-28}~\textrm{N}}{1.01 \times 10^{-67}~\textrm{N}}\\ &= 2.27 \times 10^{39}. \end{align*}$

That is, for a single proton and a single electron in a hydrogen atom, the electrostatic force is nearly 40 powers of ten stronger than the gravitational force between the two particles! (Note that the radius of the hydrogen atom, being equal for both the electrostatic and gravitational forces, cancels out in the calculation.)

The fact that the electrostatic force is so much stronger than gravity may be something that you’ve noticed, perhaps if you’ve ever stuck a balloon to the wall after rubbing it in your hair. Dr. Pasquale demonstrates this in the video below.

The force from a few charged particles on the balloon is easily able to overcome gravity. This also happens when small pieces of plastic stick to your hands. (Or when foam peanuts stick to a cat, as seen in Figure 22.1.) These situations are not defying gravity: electrical charge that’s built up on an insulator (such as foam or plastic) will cause it to have an electrostatic force with any neutral object nearby.

A photograph of a cat covered in white foam packing peanuts. — Figure 22.1 – A cat is covered in foam packing peanuts due to electrostatic attraction between the charged foam and cat’s fur. Cooper and styrofoam, by Sean McGrath, is licensed under CC BY 2.0.

The second big difference between the electrostatic force and gravity is that electrostatic forces come in two types: attractive and repulsive. There are two types of charge, and that means the force can go in one of two directions: toward and away. Meanwhile, gravity is only an attractive force. Mass can only be positive, not negative, so we will only ever experience attractive forces with other objects of mass.

When using Coulomb’s law, we need to be careful to ensure that the sign we obtain in our force calculation is consistent with the direction of that force. As described in appendix A of this textbook, vectors pointing to the right are positive, and vectors pointing to the left are negative. Vectors pointing up are positive, and vectors pointing down are negative. We will want to ensure that the direction of force corresponds with this convention.

Therefore, when calculating an electrostatic force, first calculate the magnitude of that force by using the equation. Once you’ve finished calculating the magnitude, look at the types of charges involved to determine the direction.

Consider a charge (charge A) $q_A = +10~\mu\textrm{C}$ (that is: $10 \times 10^{-6}~\textrm{C}$ ) that’s held 0.2 meters away from a second charge (charge B) $q_2 = -5~\mu\textrm{C}$ ( $-5 \times 10^{-6}~\textrm{C}$ ). What is the force that charge B causes on charge A?

First, calculate the magnitude by ignoring the signs of the charges and using Coulomb’s law.

$\begin{align*} F &= (9\times 10^9~\textrm{Nm}^2/\textrm{C}^2) \frac{(10 \times 10^{-6}~\textrm{C})(5 \times 10^{-6}~\textrm{C})}{(0.2~\textrm{m})^2}\\ &= (9\times 10^9~\textrm{Nm}^2/\textrm{C}^2) \frac{5 \times 10^{-11}~\textrm{C}^2}{0.04~\textrm{m}^2}\\ &= 11.25~\textrm{N} \end{align*}$

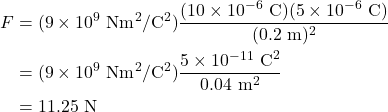
Next, analyze the situation to determine the direction of the force. Because B is causing the force, A is the charge that is moving as a result. In which direction will charge A move? Because the force is attractive (there are unlike charges involved), charge A will move toward charge B. If that direction is to the right, then the force is positive. If that direction is to the left, then the force is negative.

What is the force that charge A causes on charge B? We can solve this in two ways. The first is to see that the magnitude using Coulomb’s law will be the same, and because now B is in motion, it moves in the opposite direction as charge A. Or we can recall from Newton’s third law that these are action-reaction pairs, meaning the forces will be equal and opposite.

Conduction

Materials can be characterized by how easily they allow electrons to move around. We looked at a similar property when we learned about heat transfer. In fact, materials that are good at moving heat around also tend to be good at moving electrons around (and vice versa).

Conductors

We call materials in which electrons can easily move around electrical conductors. If you think about what wires are made of, maybe you can think of the types of materials that make good electrical conductors: metals. In metals, electrons are able to move around easily. This means we use them in all of our electric circuits (for example, the circuit in Figure 22.2) as well as in power lines and the charging cable you use for your electronic devices.

A photograph of a digital electronic circuit built on a breadboard. There are several integrated circuit chips (black rectangles with silver metal pins protruding from each side) as well as many different colored wires. — Figure 22.2 – An electric circuit built with integrated circuit chips and many wires. All of the wires are copper conductors coated with plastic insulation. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Insulators

Materials that are not good electrical conductors are called insulators. Plastic, paper, air, wood: these are all good electrical insulators. In these materials, electrons are very tightly bound to the nucleus of their host atoms. However, when water contains impurities such as salt, then it becomes a very good conductor.

In fact, the wires in the electric circuit shown in Figure 22.2 are coated with an insulator: plastic. This is to prevent the conductors inside each wire from touching each other and sending electric charges flowing through the wrong paths in the circuit. The charging cables used for your electronic devices are similarly coated in a plastic insulator. The fact that air is an insulator prevents us from getting shocked when we walk near electrical outlets!

Semiconductors

The electrical properties of some materials are somewhere in between those of a conductor and those of an insulator. Their electrons aren’t super tightly bound to the nucleus as with insulators, but they’re also not as freely flowing as with conductors. We call these materials semiconductors. Silicon is probably the most widely known elemental semiconductor. It’s used in just about every integrated circuit in every computer and electronic device. Semiconductors are useful because they can be turned into an electrical switch that turns on (acts like a conductor) or off (acts like an insulator) by applying something called voltage. These electrical switches are called transistors. If you’re reading this as an ebook, the computer or phone you’re using likely has many billions of these transistors inside of its processor.

Superconductors

Another fascinating type of material is a superconductor. Superconductors are materials that are capable of allowing electrons to flow with no resistance whatsoever; that is, no energy will be lost to heat when electrons move about in these materials. Superconductors are generally made from certain elements or ceramic materials that are cooled down to just a few kelvin. That is, only a few degrees above absolute zero!

If you’ve ever had an MRI, then you’ve benefited from technology that uses superconductors. Superconducting electromagnets are used in MRI machines. They are cooled to a low temperature using liquid helium, causing a rhythmic pumping sound in the background as the MRI machine runs.

Because these materials exhibit zero resistance at very low temperatures, widespread use of superconductors is currently impractical. In the early 1980s, a new class of superconductors whose superconducting transition temperatures were greater than 77 K (-196 °C, or -321 °F) was discovered. This temperature is significant because this meant that these superconductors could be cooled with inexpensive liquid nitrogen. However, these materials tend to be ceramics and have very poor mechanical properties. A great achievement of physics would be the creation of a room temperature (300 K) superconductor that could also be made into wires. It will likely be some time before our infrastructure will involve such materials.

Charge distribution

Charge distribution refers to how charges distribute themselves or move around in different materials. In metals, electrons are able to move about freely. This means that when electrons are introduced into a metal they can move around as needed to reduce the effect of the repulsion between each individual electron. The same situation occurs when electrons are removed from a conductor. Electrons redistribute to cause the least amount of energy due to the repulsive forces between positive charged ions.

We can see this in an electroscope, as shown in the video below. When electrons are introduced into the electroscope, which is made of metal, the free piece of metal in the electroscope moves away. Because the negative charges have distributed themselves throughout the conducting material, we can see the repulsive force causing the free piece of metal to rotate to get as far away from the surrounding negatively charged metal as possible.

The same thing occurs when electrons are removed from the electroscope, shown in the video below. The conducting material of the electroscope becomes positively charged and the repulsive force causes the free piece of metal to rotate away from the rest of the positively charged metal.

Conduction

Conduction occurs whenever two or more conducting materials come into contact with each other. Charge is able to flow freely between the conductors, causing the electrons to move in such a way as to minimize repulsive forces. We will discuss the effects of conduction much more in the next chapter of this textbook when discussing electric circuits. The flow of charge, known as current, causes many interesting electrical properties and plays a large role in our 21st century lives.

Grounding

Grounding is a special type of conduction where charges redistribute themselves to an area that can accept lots of charges without causing a large buildup of electrons or positive ions. The Earth is a great ground source. Because the Earth is so large, it can accept a lot of electrons without causing a buildup of charge. When you plug in your electronics, the ground connection to the earth is provided by either a copper wire connected to plumbing (as in Figure 22.3), or a copper wire buried in the ground.

A photograph of a copper pipe plumbing system. There are a few pipes connected together that continue through the concrete floor, presumably into the Earth beneath. An electrical wire is connected to the plumbing, creating an Earth ground connection. — Figure 22.3 – A copper plumbing pipe connected to the Earth has an electrical ground wire connected to it. Metal water pipe used as grounding electrode, by z22, is licensed under CC BY-SA 3.0.

Sometimes, grounding can occur through our bodies. Humans are relatively good conductors. When Dr. Pasquale touches the electroscope in the video below, charges move around to the ground through her hand and her skin. We can see that she has discharged the electroscope as the freely moving piece has rotated back to its equilibrium position. There is no longer a charge on the metal causing a repulsive force.

As long as there isn’t too much charge flowing through a person when they act as a conduit to ground, this can be safe. This becomes very dangerous only when the flow (movement) of charge becomes too high. The mere presence of charge is not in itself dangerous.

In the video below, Dr. Pasquale holds onto a van de Graff generator. As it runs, electrons build up on her skin and hairs. After a time, we can visually see the effect of this charge buildup as her hairs begin to separate from each other: they are experiencing the force of electrostatic repulsion. The hair on her head and on her skin will stick up.

When Dr. Pasquale sticks her finger out, a corona discharge emanates from her finger. This is caused by the air around her finger becoming ionized. Unfortunately, the sound was not captured well enough on the video above to hear. If you have ever stood in the vicinity of large transmission lines, the corona discharge sounds like a staticky hiss.

Note that a lot of electric charge transfers to Dr. Pasquale’s body when she touches the van de Graff generator. As long as she does not let that charge flow rapidly away from her, this is perfectly safe. She stands on a giant plastic block when she is touching the van de Graff generator so that charge cannot flow through her feet into the floor. She is surrounded by insulators. The van de Graff generator would be dangerous if Dr. Pasquale were to touch an object and cause the electrons to flow through her body.

At the conclusion of the video, Dr. Pasquale is grounded when she touches a wire connected to a very large resistor. This electrical component, which will be discussed in the next chapter of this book, ensures that the charge does not flow away from her body too fast. It causes the charge to flow away at a safe rate.

Electrostatic discharge

While the presence of charge in itself is not a danger, the movement of charges, known as current (which will be discussed in the next chapter of this textbook) is where the danger lies. Perhaps you can recall being shocked while touching a doorknob after walking across a carpeted floor in the winter. This shock (known as electrostatic discharge), does not come from the charge buildup itself, but from the movement of that charge when it is able to discharge from your body.

We can see electrostatic discharge using a Wimshurst machine, as shown in the video below. Rotating the machine causes a buildup of opposite charge on the two spheres. As long as the charge remains surrounded by insulators, it will remain on the metal sphere. As soon as a second sphere comes close enough, the charge will discharge, even through the gap of air in between the two spheres! Dr. Pasquale filmed this demo with the lights off to make the sparks easier to see.

In insulating materials, charges cannot move around freely. Charges will tend to stay where they are placed. When rubbing a balloon in your hair, electrons are transferred to the balloon. Because the balloon is made of an insulating material, the electrons are unable to redistribute around the entire balloon. Only the portion of the balloon that was rubbed against your hair is able to stick to the wall. The other side of the balloon does not have a buildup of electrons and remains neutral. This side of the balloon will not stick to the wall.

Induction

Induction is another way that charges can be caused to redistribute themselves in different materials. Unlike conduction, induction does not always require physical contact between objects to cause charges to move.

In the video below, we can see how charges redistribute when Dr. Pasquale holds a negatively charged (gray PVC) rod close to (but not touching) the top of the electroscope. The charged rod is not touching any of the metal contacts, but we can see from the movement of the metal piece in the electroscope that charges are moving around. Electrostatic repulsion causes electrons to move to the bottom of the electroscope, to be as far away from the negatively charged rod as possible. While the net charge on the electroscope is still zero, there is an overall polarization of the metal. The abundance of negative charges in the bottom of the electroscope causes repulsion (see Figure 22.4, left), and the movable piece rotates as a result of that force. When the charged rod is moved away from the electroscope, the effect goes away.

The same effect occurs with a positively charged rod (shown in the video above with the clear acrylic rod). When holding it close to (but not touching) the top of the electroscope, the electrons experience an attractive force, causing them to move to the top of the electroscope. This creates a buildup of positive charge in the bottom of the electroscope (see Figure 22.4, right), causing the moveable piece to rotate as a result of the repulsion between these positive charges.

Two photographs of an electroscope. On the left is an electroscope with a negatively charged PVC rod held close to, but not touching, the top of the electroscope. The freely rotating piece of metal has rotated, demonstrating electrostatic repulsion. Annotated on the diagram are the electrons (negative charges) populating the rod and the base of the electroscope. On the right is an electroscope with a positively charged acrylic rod held close to, but not touching, the top of the electroscope. The freely rotating piece of metal has rotated, demonstrating electrostatic repulsion. Annotated on the diagram are the positive ions populating the rod and the base of the electroscope. — Figure 22.4 – Induction in metals occurs due to charge redistribution in the conducting material from electrostatic repulsion. This can occur due to the presence of a negatively charged object (left) or a positively charged object (right). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Charging by induction

If we want to use this effect to cause a more permanent charge in metals, we can use two pieces of metal instead of one. Placing a negatively charged object nearby two touching metal objects will cause the charges in the metal to redistribute. Repulsion causes the electrons in the metal to move as far away from the charged object as possible. As a result, the metal closest to the charged object will now contain a positive charge (Figure 22.5, left). If the two metal objects are then separated, and the charged object moves away, we are left with two charged pieces of metal (Figure 22.5, right). Each piece now holds an opposite charge of equal magnitude. This process is known as charging by induction.

Induction in insulators (polarization)

Induction can also occur in insulators, but the effect is slightly different due to the fact that electrons cannot move around freely in insulators. If we could look at the arrangement of the molecules surrounding the balloon sticking to the wall (as in the video earlier in this chapter), we would see that while the electrons cannot move, the molecules will become polarized. In effect, the molecules reorient themselves so that the negatively charged parts of the molecules are as far from the balloon’s negative charges as possible. This is shown in Figure 22.6.

A diagram of the negative charges that have accumulated on the side of the balloon, and the molecules in the whiteboard adjacent to the balloon. The molecules in the whiteboard realign themselves so that their positive charges are closer to the balloon. — Figure 22.6 – The negative charges in the balloon cause the molecules in the whiteboard to realign themselves to minimize electrostatic repulsion. Note: this diagram is not to scale. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

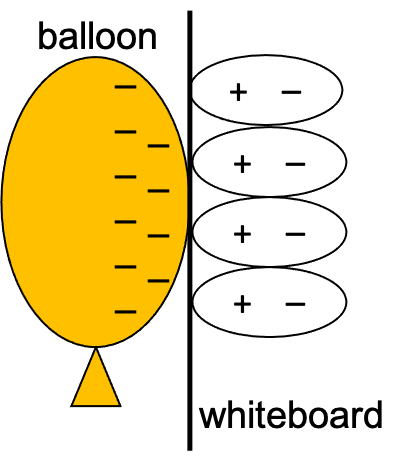
These explanations of induction in metals and insulators explains a phenomenon we saw earlier in this chapter in the video of the charged rods attracting the meter stick: charged objects are attracted to neutral objects. Note in Figure 22.6 that the positive charges in the wall are closer to the negative charges on the balloon due to electrostatic attraction and that the negative charges in the wall are farther from the negative charges on the balloon due to electrostatic repulsion. Since the electric force between single electric charges varies inversely as the square of the distance between them, the force weakens more quickly than the distance increases. This means that the attraction is greater than the repulsion, so the balloon sticks to the wall. If a positively charged object is brought near the neutral wall, the atoms in the wall will polarize the opposite way. Either way, the attractive force outweighs the repulsion. Again, charged objects attract neutral objects.

Electric fields

Recall from chapter nine that fields are a model that allows us to see how objects in the presence of forces will interact. An electric field shows us how charged objects will interact as a result of electrostatic forces. We can draw an electric field by showing how a positively charged object would move as a result of being in the presence of another charged object.

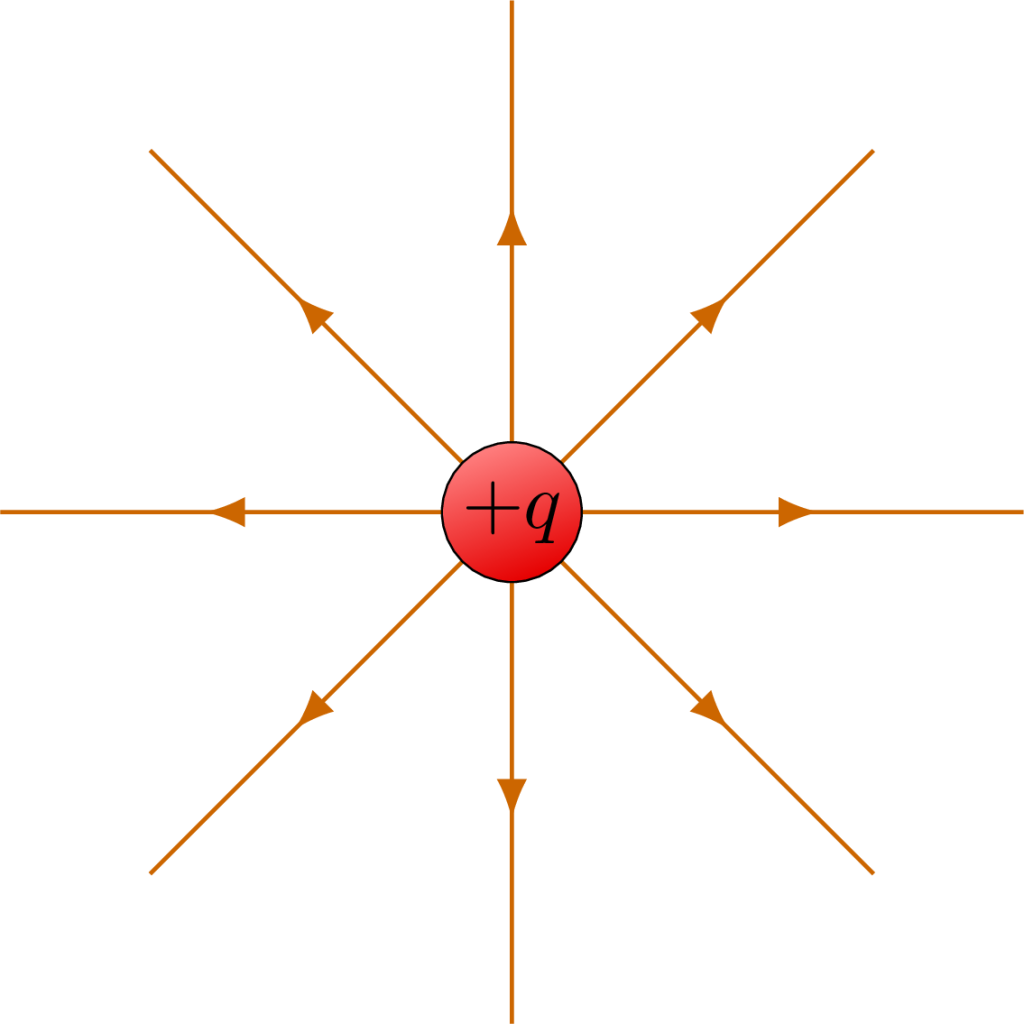
The electric field of a charge distribution can be mapped by noting the trajectory that a small (so as not to affect the electric field of the charge distribution) positive test charge follows when placed at various points in space around the charge distribution. In the simplest case, we can draw the electric fields corresponding to single point charges. The electric fields shown in Figure 22.7 emanate symmetrically from a single positive charge. Because fields depict how a positive charge would move if placed near this single positive charge, they must depict the force of repulsion and indicate movement away from the positive charge. The arrows depicted on the field point away from the center as a result. Note that there are really an infinite number of electric field lines from any charge distribution and that any diagram will show just a few representative lines.

A diagram of the field lines emanating from a positive point charge. — Figure 22.7 – A positive point charge has electric field lines that point radially away. Positive point charge, by Izaak Neutelings, is licensed under CC BY-SA 4.0.

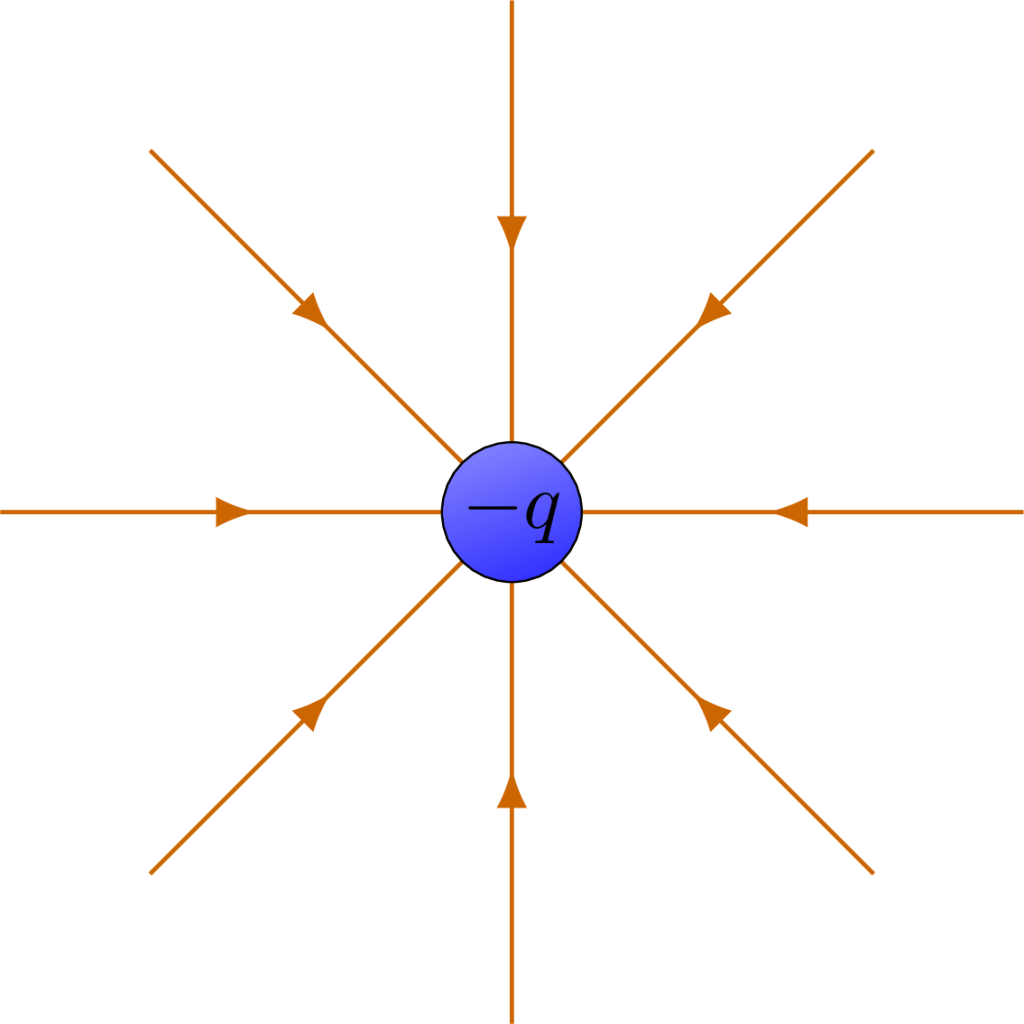
The electric fields shown in Figure 22.8 surround a single negative charge. Because field lines depict how a positive charge should move if placed near this negative charge, they depict the force of attraction and indicate movement toward the negative charge. The arrows depicted on the field point toward the center as a result.

A diagram of the field lines emanating from a negative point charge. — Figure 22.8 – A negative point charge has electric field lines that point radially toward the center. Negative point charge, by Izaak Neutelings, is licensed under CC BY-SA 4.0.

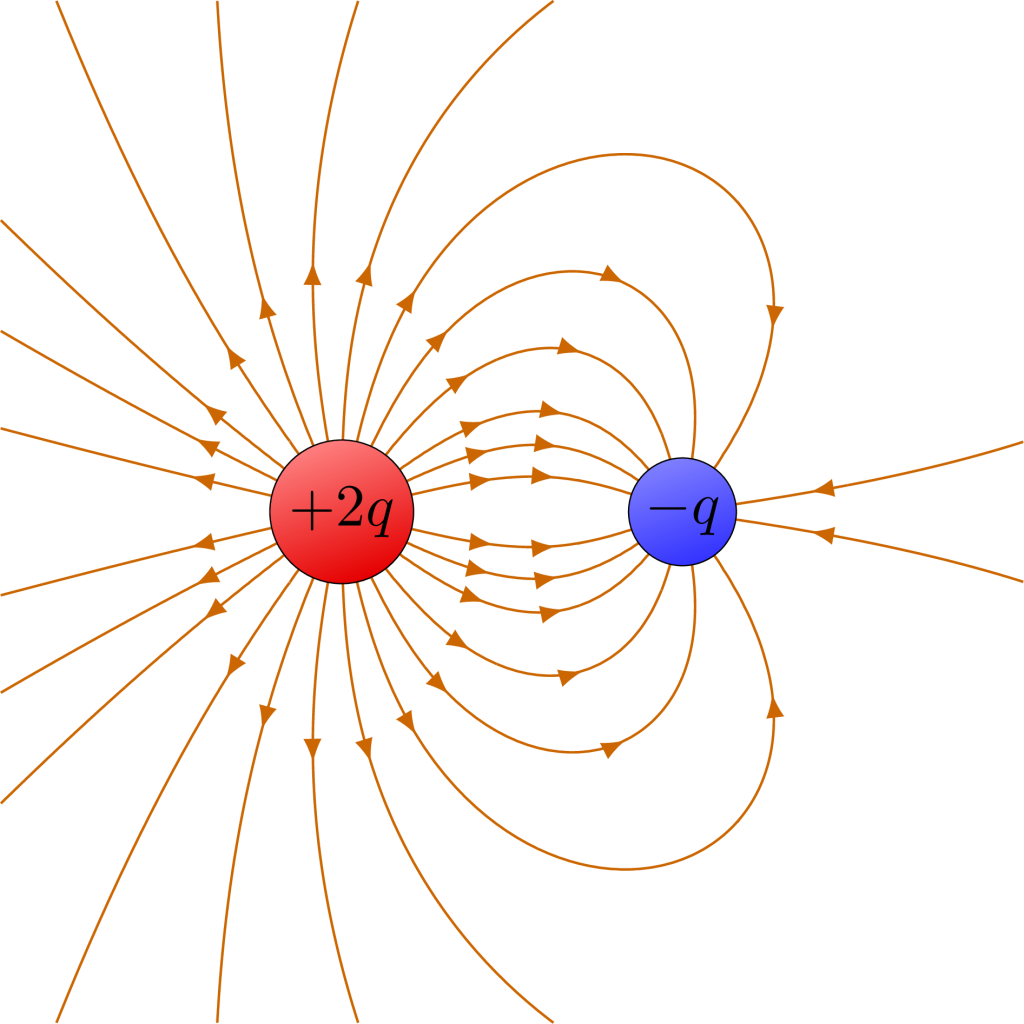
Electric field diagrams can be drawn for more complicated arrangements of charges, and serve as a useful model for us to determine how positive charges would move in these scenarios. (For example, the electric field lines between two attracting point charges are shown in Figure 22.9.) In addition, just as the gravitational forces are strongest when the gravitational field shows the arrows closest together, the electrostatic forces are strongest when the electric field arrows are closest together.

A diagram of the field lines between two attracting point charges. — Figure 22.9 – Two attracting point charges have a more complicated electric field diagram. The field lines always point away from positive and toward negative charges. Attracting point charges, by Izaak Neutelings, is licensed under CC BY-SA 4.0.

Electric potential

Just as objects of mass in the presence of a gravitational field have gravitational potential energy, charged objects in the presence of an electric field have electric potential energy. This stored energy can be used to do useful work: charge your cell phone, turn on your lights, or run your refrigerator. We use EPE as the symbol for electric potential energy. Because it is a form of energy, we use joules as the unit. The equation for electric potential energy is

$EPE = k \frac{q_1q_2}{d}.$

This describes the energy stored as the result of holding two charges ( $q_1$ and $q_2$ ) a distance $d$ apart from each other. The variable $k$ in the equation is Coulomb’s constant, defined earlier in this chapter.

Even if there are not two charges, the presence of a single charge creates electric potential, the possibility to create electrical energy. There doesn’t have to be a second, or third, or fourth charge around to interact with the electric field caused by the first one. Electric potential is equal to

$EP = k\frac{q}{d},$

which can be seen as equal to $EPE$ divided by charge.

Electric potential can also be defined as describing the amount of work it takes to move a charge through an electric field, divided by the amount of charge. This definition helps to describe the units for electric potential: joules (work) divided by coulombs (charge). A J/C is also equal to a volt (defined by the capital letter V). This concept of potential is very important in electronics. A difference in electric potential between two points is known as voltage.

The quantities of electric potential energy ( $EPE$ ) and electric potential ( $EP$ ) are analogous to the quantities of gravitational potential energy ( $GPE$ ) and gravitational potential ( $GP$ ). This is described in the table below.

	gravitational	electric
potential energy	$GPE = mgh$	$EPE = k\frac{qq_1}{d}$
potential	$GP = \frac{GPE}{m} = gh$	$EP = \frac{EPE}{q_1} = k\frac{q}{d}$

Practice questions

Numerical analysis

If charge A of +5 µC is placed 2 meters away from charge B of -3 µC, calculate the magnitude of the electrostatic force between the two charges. If charge A is located to the left of charge B, determine the direction that…
1. …charge A would move due to charge B.
2. …charge B would move due to charge A.
If charge A of +8 µC is placed 5 centimeters away from charge B of +12 µC, calculate the magnitude of the electrostatic force between them. If charge A is located to the left of charge B, determine the direction that…
1. …charge A would move due to charge B.
2. …charge B would move due to charge A.
Two electrons, each with a charge of 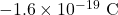$-1.6 \times 10^{-19}~\textrm{C}$ , are separated by a distance of 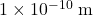$1 \times 10^{-10}~\textrm{m}$ . Calculate the magnitude of the electrostatic force between them.
Three point charges are placed in a straight line with equal separations of 0.1 meters between each charge. The charges are +6 µC (left), -2 µC (middle), and +8 µC (right). Calculate the net electrostatic force on the…
1. …+6 µC charge due to the other two charges.
2. …-2 µC charge due to the other two charges.
3. …+8 µC charge due to the other two charges.

Hands-on experiments

Rub a piece of plastic with a paper towel or piece of cloth and then bring it close to small pieces of paper or a small piece of thread. Observe how the plastic attracts the paper or thread.
Charge a plastic comb (or other plastic object such as a balloon) by rubbing it with a cloth and then bring it close to a stream of water without touching it. Observe how the water stream bends towards the comb. This shows the attraction between the charged comb and the water.
Try the balloon on the wall experiment: Inflate a balloon and rub it against your hair or clothing to create a static charge. Then, stick the balloon to the wall and observe how it clings to the wall due to electrostatic forces.

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Charge

Coulomb’s law

Conduction

Conductors

Insulators

Semiconductors

Superconductors

Charge distribution

Conduction

Grounding

Electrostatic discharge

Induction

Charging by induction

Induction in insulators (polarization)

Electric fields

Electric potential

Practice questions

Numerical analysis

Hands-on experiments

License

Share This Book