9. Gravity
Summary
Apparent weight
Weight is a topic that we’ve discussed several times already in this textbook. We’ve learned that weight is a force that comes about due to our gravitational attraction with the Earth, and that it’s related to our mass. While none of that is wrong, it’s also not the full story of what weight is.
As you read this textbook, consider where you feel your weight in your body. Where does the sensation of weight come from right now? If you’re standing, you can probably feel your weight in your feet. If you are sitting, you likely feel your weight in your bottom and the backs of your thighs. If you are lying down, you likely feel your weight along your side or back.
We have weight because of gravity, but our apparent weight comes from the support force we get from whatever surface we’re in contact with. Our apparent weight is equal to the value of the support force that is acting on us.
In the video below, Dr. Pasquale jumps up and down on a force plate. The force that is measured by the plate is recorded by LoggerPro on the laptop in the background. This recording is also shown in Figure 9.1.
When Dr. Pasquale is standing still, her weight records as being constant. However, when she jumps up and down, her weight changes. When she is in the air, she is no longer in contact with the force plate, and her weight is zero. When she is coming back to the surface again, her weight increases. This demonstration shows that weight is not necessarily constant, even while being located in pretty much the same position on the Earth’s surface.
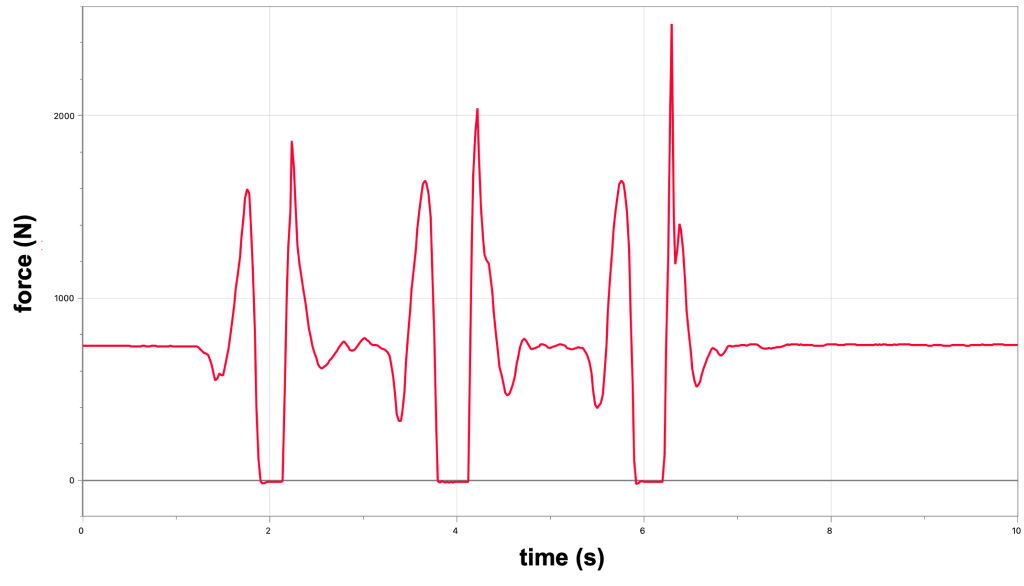
Any time our motion contains a vertical component of acceleration, whether it be from jumping up and down, riding a roller coaster, or traveling in an elevator, our support force will change, and our apparent weight will change as well.
Consider a hypothetical person (let’s call her Jane Physics) riding in an elevator. Any time the elevator moves at a constant speed, there is no acceleration in the vertical direction, and Jane’s apparent weight will be equal to the force of gravity that is acting on her mass. Because the net force acting on Jane is zero, her support force must be equal and opposite to her gravitational force. The support force is therefore equal to her mass times gravitational acceleration.
In general, we can relate the net force, support force, and force of gravity by using an equation. Remember that net force is equal to the sum of all forces (in this case, there are two forces: gravity and the support force). Therefore,
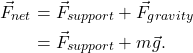
Gravitational acceleration is -9.8 m/s2. Because we are dealing with vectors in the above equation, that negative sign on ![]() is very important!
is very important!
Now consider Jane Physics riding in an elevator that is speeding up as it moves upward. Because the elevator is speeding up in the upward direction, there is an upward acceleration, and a net force pointing up. Her mass hasn’t changed, so the ![]() term in the above equation remains the same. The support force now becomes greater than her weight. This is because
term in the above equation remains the same. The support force now becomes greater than her weight. This is because ![]() (gravitational force) plus the support force equals the resultant force, that net upward force causing the elevator to speed up. This is why apparent weight increases as we speed up in an elevator moving upward.
(gravitational force) plus the support force equals the resultant force, that net upward force causing the elevator to speed up. This is why apparent weight increases as we speed up in an elevator moving upward.
If Jane Physics has a mass of 75 kg, her weight in an unaccelerated condition is
![]()
If the elevator accelerates upward at a rate of 4 m/s2, then Jane’s net force is equal to her mass times the acceleration of the elevator,
![]()
Solving the equation above to solve for the support force, we can calculate Jane’s apparent weight to be
Jane Physics reaches the top floor of the building and decides to ride back down to the lower level. At this time, the elevator will speed up moving downward. There is a downward pointing acceleration, and therefore, a net force pointing down. The support force becomes less than Jane’s weight. This is why apparent weight decreases as an elevator speeds up moving downward.
Jane’s unaccelerated weight is -735 N. If the elevator accelerates downward at a rate of 3 m/s2, then Jane’s net force is
![]()
We can solve for Jane’s apparent weight by using the above equation, solved for the support force.
![]()
Note that Jane’s apparent weight is now less than her unaccelerated weight.
Free fall
The extreme condition of this would be a situation where the elevator cable snaps and the elevator moves downward at 9.8 m/s2: free fall. In that case, Jane’s apparent weight would go to zero! While this should never happen in an elevator, it’s possible that you may have experienced such a condition of weightlessness in an amusement park ride.
An object in free fall, moving only under the influence of gravity with no other forces present, will have an apparent weight of zero. If you were to go skydiving, before the parachute deploys, and before air resistance slows you down, your apparent weight would be zero. Think about using a scale to measure your weight as you fall: there is nothing to give the scale a force reading. In those conditions you are truly weightless.
For the same reasons, astronauts in Earth orbit (whether they be in a space capsule, the Space Shuttle, or the space station) are also weightless, as shown in Figure 9.2. They are still under the influence of Earth’s gravitational field, and their acceleration due to gravity is still rather high (about 9 m/s2). The reason that astronauts experience weightlessness is that they are in free fall around the Earth during their orbit. To emphasize: astronauts in Earth’s orbit do not experience a zero-gravity condition, only a zero-support force condition.

The inverse-square law
The inverse-square law describes physical properties that decrease when the distance between two objects, or the distance away from a single object, increases. As distance increases, the physical property decreases. Furthermore, the property doesn’t just decrease proportionally with distance. Rather, it decreases with the square of the distance. This means that changes in distance have a very powerful effect on the physical property. Mathematically, we can represent the inverse-square law as a statement that a property is proportional to one divided by the distance squared,
![]()
A graph of a property that has an inverse-square law relationship is shown in Figure 9.3. (Note that there are no units on either axis of the graph in Figure 9.3 because the relationship between the physical property and distance is arbitrary in this case.)
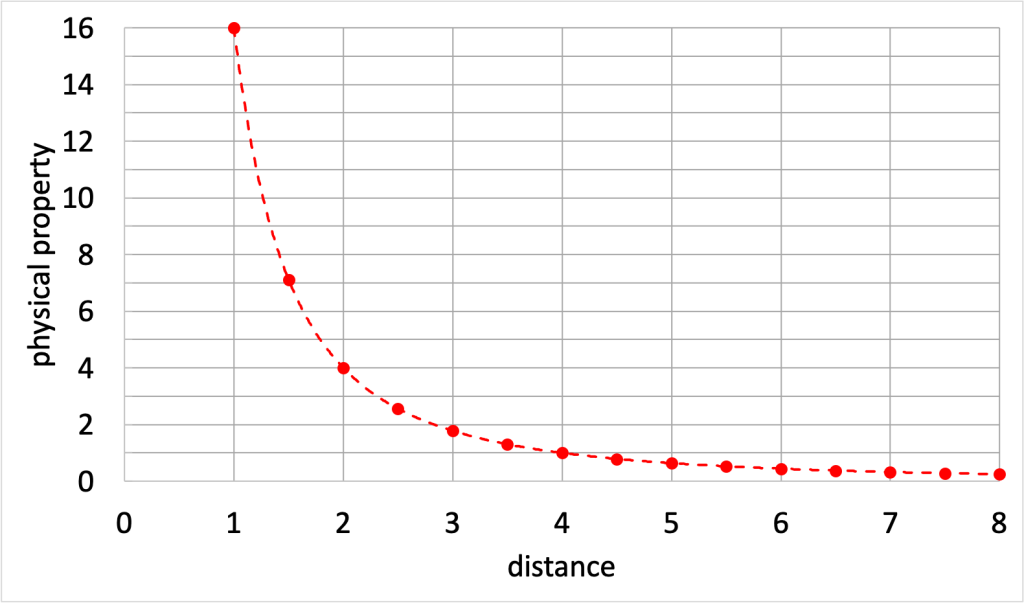
The graph in Figure 9.3 can be used to help conceptualize the effect of distance on a property that obeys the inverse-square law. When the distance between the objects is equal to one, the physical property in this case is 16. When the distance doubles (becomes equal to 2), the physical property decreases by 22 and becomes 16/4 = 4. When the distance doubles again (from 2 to 4), the physical property decreases by 22 again, and becomes 4/4 = 1.
Many physical properties obey the inverse-square law: light intensity, sound intensity, electromagnetic and gravitational forces. On a conceptual level, this is because the effect of any single point of sound, light, electric charge, or mass dilutes by the distance squared as it moves outward in three-dimensional space.
Newton’s law of universal gravitation
Newton’s law of universal gravitation describes how we can quantify the force of gravity acting between any two objects in the universe. The equation states that
![]()
In other words: gravitational force (![]() ) is equal to the universal gravitational constant (
) is equal to the universal gravitational constant (![]() ), times the mass of one object (
), times the mass of one object (![]() ), times the mass of the second object (
), times the mass of the second object (![]() ), divided by the distance between the two objects (
), divided by the distance between the two objects (![]() ) squared.
) squared.
The universal gravitational constant, ![]() (sometimes known as “big G,” as opposed to
(sometimes known as “big G,” as opposed to ![]() , “little g”), is
, “little g”), is
![]()
The term universal indicates that this number is the same anywhere in the universe. It’s a very small number, indicating that the force of gravity is relatively weak. In fact, of the four fundamental forces, gravity is the weakest! In order for the force of gravity to be noticeably strong, one or both of the objects must have a lot of mass.
Note that this equation obeys the inverse-square law. If the distance between two objects were to double, the gravitational force would decrease by one fourth. If the distance between two objects were to be cut in half, the force would increase four times.
The denominator of this equation tells us another interesting thing about gravity: the force of gravity between two objects cannot become exactly equal to zero unless the distance between the two objects is infinite. Therefore, it can be concluded that all objects of mass that exist in the universe exert gravitational forces on each other. A planet millions of light-years away from you is exerting a gravitational force on you. However, the value of that force is infinitesimally small. We can effectively treat it as being zero, but it is not exactly zero.
The distance between two objects is more accurately stated as the distance between the center of mass of two objects. Although the density of the Earth is not constant, if we could approximate the Earth as being perfectly spherical and having a uniform density throughout, we would expect the gravitational force to not change as we move along the Earth’s surface.
However, the Earth is not a perfect sphere. (The shape of the Earth is better described as an oblate spheroid.) The distance between the center of the Earth and the north and south poles is smaller than the distance between the center of the Earth and the equator (shown in Figure 9.4). Therefore, the force of gravity would be larger at the poles.
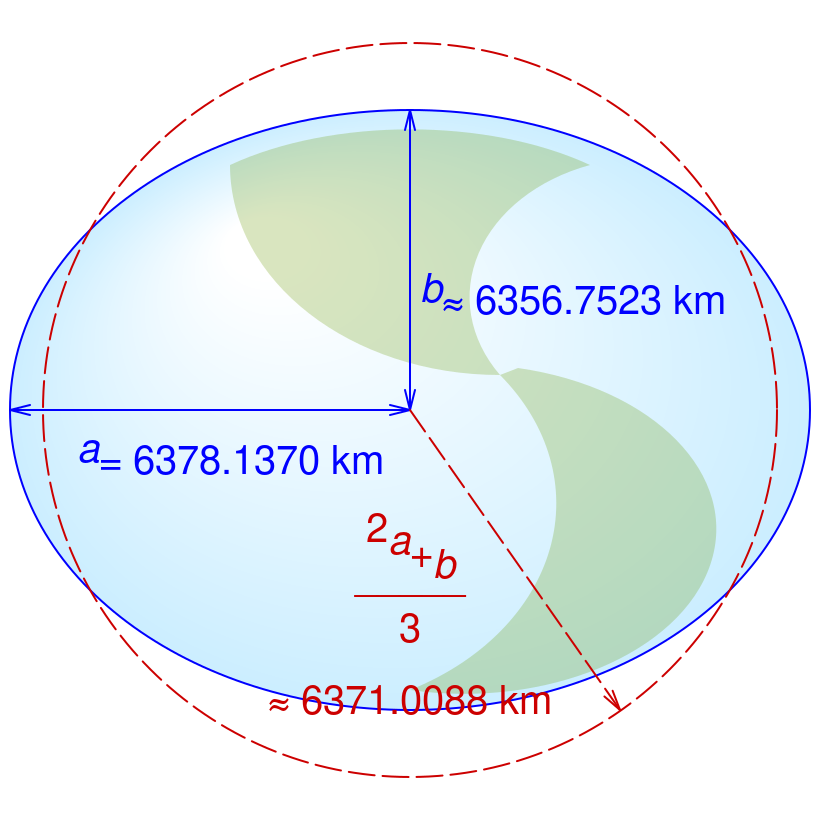
In addition, as we move farther away from the center of the Earth, say, by climbing a mountain, the gravitational force would decrease as well. It is important to point out that these differences (due to the oblateness of the Earth, and due to distance from sea level) are very small, and would not be perceptible unless you had a very accurate scale to stand on to weigh yourself.
These effects are further complicated by the fact that the Earth does not have a uniform density throughout its volume. For the most part, we can treat the gravitational force at all points on the surface of the Earth as approximately equal, but it is important to note that it is not.
In fact, astronauts visiting the space station are still under the influence of gravity – that is why the space station is able to orbit the Earth. Without gravity, no force would be able to create a centripetal force to cause objects to orbit, and they would not be able to move in a circular path. The astronauts experience weightlessness because of the lack of a support force.
One last interesting thing about gravity: because mass can only come in positive numbers, gravity is only an attractive force. When we learn about electricity later in this textbook, we’ll see that electric charges are capable of both attracting and repelling. However, the force of gravity is only an attractive force, causing two objects to accelerate toward each other, but never away.
Newton’s law of universal gravitation can be used to calculate the gravitational force acting between the Sun and the Earth. The Earth has a mass of ![]() . The Sun has a mass of
. The Sun has a mass of ![]() . The Earth and Sun are separated by a distance of
. The Earth and Sun are separated by a distance of ![]() . Using the equation above, we calculate that
. Using the equation above, we calculate that
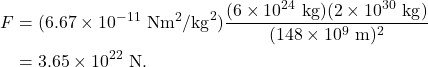
It’s also possible to use Newton’s law of universal gravitation to determine the effect that a change in properties will have on the force of gravity between two objects. For example: consider two planets with masses of ![]() and
and ![]() that are separated by a distance of
that are separated by a distance of ![]() . (The exact values do not matter in this case.)
. (The exact values do not matter in this case.)
If the mass of planet one (![]() ) were to be cut in half, what would the effect be on the force? Force and mass are directly proportional. Therefore if the mass decreases by a factor of two, the force will decrease by a factor of two as well. The new force would be one half of the original force.
) were to be cut in half, what would the effect be on the force? Force and mass are directly proportional. Therefore if the mass decreases by a factor of two, the force will decrease by a factor of two as well. The new force would be one half of the original force.
If instead, the masses of both planets stay the same, but the distance between the two planets is cut in half, what is the effect on the gravitational force? Force and distance obey the inverse-square law. If the distance between the two planets decreases by a factor of two, the force will increase by a factor of two-squared: four. The new force would be equal to four times the value of the original force.
Gravitational acceleration
In this textbook, we have frequently encountered “little g,” the acceleration due to gravity on the Earth’s surface. This quantity has a value of -9.8 m/s2. (Sometimes, when we do not need great accuracy in our calculations, we can round “little g” to -10 m/s2.) Where does this number come from?
From Newton’s second law, we know that the net force on an object is equal to its mass times its acceleration. If the net force on an object comes from gravity, then we can use Newton’s second law and Newton’s law of universal gravitation together, and solve for the acceleration. In this case,
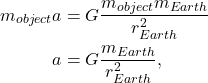
where ![]() is the acceleration of any object on the Earth’s surface,
is the acceleration of any object on the Earth’s surface, ![]() is the universal gravitational constant,
is the universal gravitational constant, ![]() is the mass of the Earth, and
is the mass of the Earth, and ![]() is the radius of the Earth. The distance between the surface of the Earth and the center of mass of any object on Earth is infinitesimally small compared to the radius of the Earth itself and will be ignored in this textbook.
is the radius of the Earth. The distance between the surface of the Earth and the center of mass of any object on Earth is infinitesimally small compared to the radius of the Earth itself and will be ignored in this textbook.
When an object is, say, orbiting the Earth, then the distance between the surface of the Earth and the center of mass of the object h will become an important quantity to be considered in the equation. In this case, the equation will become
![]()
where ![]() is the mass of the Earth,
is the mass of the Earth, ![]() is the radius of the Earth, and
is the radius of the Earth, and ![]() is the distance between the surface of the Earth and the center of mass of the object (satellite, space station, etc.).
is the distance between the surface of the Earth and the center of mass of the object (satellite, space station, etc.).
Gravitational acceleration, being a particularly important quantity, is given its own symbol: ![]() . In the equation, the mass of the object canceled out on both sides of the equation. This means that gravitational acceleration acts equally on all objects on the Earth’s surface: you, an airplane, a butterfly, a tree, or a house.
. In the equation, the mass of the object canceled out on both sides of the equation. This means that gravitational acceleration acts equally on all objects on the Earth’s surface: you, an airplane, a butterfly, a tree, or a house.
This equation can be solved to find the value that we have seen so many times so far in this textbook. The mass of the Earth is ![]() kg, and the radius of the Earth is
kg, and the radius of the Earth is ![]() m. Therefore,
m. Therefore,
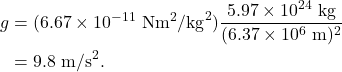
Gravitational acceleration at different heights above the Earth’s surface
Gravitational acceleration at sea level is 9.81 m/s2. What is the gravitational acceleration at the top of Mount Everest?
When using the equation in this manner, the mass of the Earth is treated as a constant, but the distance will be equal to the radius of the Earth plus whatever distance away the object is from sea level.
The summit of Mount Everest is located approximately 8,850 m above sea level. Plugging that in to our equation, we find that
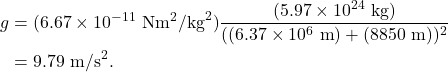
The result, 9.79 m/s2, is not a big difference from sea level! This goes to show that we can treat “little g” as a constant of 9.8 m/s2 for the entire surface of the Earth if precision is not important in our calculations (which it will not be in this textbook).
To calculate the value of the gravitational acceleration on a different celestial body (the Moon, the Sun, or another planet), simply use Newton’s law of universal gravitation and Newton’s second law. In general,
![]()
where ![]() is the mass of the celestial body, and
is the mass of the celestial body, and ![]() is the radius of the celestial body. The universal gravitational constant (“big G”) is equal everywhere in the universe.
is the radius of the celestial body. The universal gravitational constant (“big G”) is equal everywhere in the universe.
The gravitational acceleration on Mars is less than that of Earth. Mars has a mass of ![]() kg and a radius of
kg and a radius of ![]() m. We can plug these values into the equation and find that
m. We can plug these values into the equation and find that
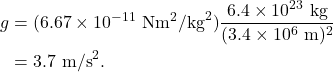
If Mars were to magically double in mass, what would the effect be on the gravitational acceleration? Gravitational acceleration is directly proportional to mass. Therefore, if mass doubles, “little g” doubles as well. If Mars were to magically double in mass, its gravitational acceleration would become 7.4 m/s2.
What if instead of Mars’s mass magically changing, its radius expands until the planet has double the radius? What effect would that have on the gravitational acceleration? The relationship between “little g” and the radius obeys the inverse-square law. Therefore if the radius increases by a factor of two, the gravitational acceleration will decrease by a factor of two-squared: four. In that case, “little g” on Mars would decrease to 0.9 m/s2.
Gravitational fields
A gravitational field is a model that we can use to describe how objects interact as a result of gravitational forces. We can draw a gravitational field by showing where any object placed around a massive object would move due to gravity.
Consider the gravitational field of the Earth. Any object of mass is going to want to move toward the center of the Earth. This is depicted by showing the field using arrows pointing toward the center of the Earth.
In Figure 9.5, the gravitational field is depicted around the Earth. (In reality, the field is three-dimensional, but it is difficult to convey that in a two-dimensional format such as a computer screen or printed sheet of paper.)

At any given distance away from the center of the Earth, the distance between each of the field lines is proportional to the relative strength of the force. Close to the center of the Earth, the arrows are much closer together than they are far away from the center of the Earth. This means that gravitational forces are stronger closer to the center of the Earth, and weaker farther away. This makes sense based on our understanding of the inverse-square law.
Gravitational potential energy in a nonuniform gravitational field
Up until this point, we have calculated the gravitational potential energy of an object to be ![]() where
where ![]() is the mass of the object,
is the mass of the object, ![]() is the acceleration due to gravity, and
is the acceleration due to gravity, and ![]() is the height above the reference level. The reference level is the location at which the object would have zero gravitational potential energy measured with respect to that height. The choice of reference level is arbitrary as long as it is consistent for all subsequent measurements or calculations.
is the height above the reference level. The reference level is the location at which the object would have zero gravitational potential energy measured with respect to that height. The choice of reference level is arbitrary as long as it is consistent for all subsequent measurements or calculations.
When throwing a ball in the air, the reference level may be the ground. For a swinging pendulum, the reference level may be the bottom of the swing. For a cart rolling down an incline on a tabletop, the reference level may be the position of the tabletop at the bottom of the incline. These selections are chosen because when we are performing calculations in these scenarios, the exact amount of GPE is less important than the transformation of GPE into other forms of energy (in particular: kinetic energy).
For example, consider a ball with a mass of 1 kg that is initially at rest and dropped from a height of 10 m above the ground. If the reference level is considered to be the position of the ground, then the ball starts with 98 J of GPE and 0 J of KE (because it is initially at rest). At the instant before the ball hits the ground, the height above reference is zero and GPE is equal to 0. The KE of the ball is 98 J (which can be calculated using conservation of mechanical energy or with the kinematic equations introduced in chapter 3).
However, if the reference level is considered to be the initial position of the ball, then the ball starts with 0 J of GPE and 0 J of KE. At the instant before the ball hits the ground, the GPE of the ball is -98 J (the negative sign is because the ball is below the reference point) and the KE of the ball is 98 J. Regardless of our selection of the reference level, the KE of the ball at any point will be the same.
The acceleration due to gravity, introduced earlier in this chapter, has an inverse-square relationship with the distance between the object of mass and the center of mass of the celestial object. We saw that on Earth, the acceleration due to gravity is 9.8 m/s2 at sea level.
As long as the altitude (height) or trajectory of an object is small compared to the radius of the celestial body (as is the case when tossing a ball into the air or swinging a mass on a pendulum), then g is approximately constant and the expression ![]() is sufficiently accurate. However, if the trajectory of the projectile causes a significant enough altitude change (even just 1% of the radius of the celestial body), then the value of
is sufficiently accurate. However, if the trajectory of the projectile causes a significant enough altitude change (even just 1% of the radius of the celestial body), then the value of ![]() will not be constant along the trajectory of the object’s motion, nor will it necessarily be equal to the value of 9.8 m/s2 that we have used so far in this textbook. Treating
will not be constant along the trajectory of the object’s motion, nor will it necessarily be equal to the value of 9.8 m/s2 that we have used so far in this textbook. Treating ![]() as a fixed value equal to 9.8 m/s2 will therefore yield an incorrect calculation for GPE.
as a fixed value equal to 9.8 m/s2 will therefore yield an incorrect calculation for GPE.
In such circumstances, the correct formula for the gravitational potential energy of an object having a mass of m that is a distance r from the center of the celestial body is
![]()
Note that the equation contains a negative sign, resulting in a negative value for GPE. This is because the equation assumes that the reference location is the position where the object is positioned infinitely far away from the celestial body.
Consider a mass m held 10 m above the ground compared to an identical mass held 20 m above the ground. The GPE of the mass closer to the ground should be less than that of the mass that’s higher up. In other words, the farther apart the mass and the celestial body are from each other, the greater the GPE.
If we were to calculate the GPE of both masses using the equation above without a negative sign, we would find that the value of GPE for the mass held at 20 meters above the ground would be larger than that of the mass held at 10 meters above the ground! This doesn’t make sense. The negative sign ensures that the value of GPE becomes larger (less negative) as the objects move farther apart.
In fact, the maximum value of GPE should occur when a mass is infinitely far from the celestial body. As ![]() in the denominator of the GPE equation gets larger and larger, the magnitude of the gravitational potential energy gets smaller and smaller. The negative sign in the equation ensures that this property is satisfied.
in the denominator of the GPE equation gets larger and larger, the magnitude of the gravitational potential energy gets smaller and smaller. The negative sign in the equation ensures that this property is satisfied.
The limits of Newton’s laws
Newton’s laws do a really great job of explaining the motion of so many objects. But there starts to be a discrepancy that becomes apparent when objects move fast – close to the speed of light. In these cases, Newton’s laws break down and we require another physical theory to take over. Einstein’s theory of general relativity can be used to accurately describe the forces and motions of objects in these cases.
The theory of general relativity explains the motion of objects due to curves in spacetime, the fabric of the universe. A massive object causes a large curving of spacetime, and anything moving near that massive object is going to travel along spacetime in a curved direction.
It’s possible to conceptualize this by using a model of the universe. Here, the fabric of spacetime is literally a piece of fabric stretched along a circular frame. When no massive objects exist to cause any curves in spacetime, marbles that move through space travel in straight lines, shown in the first part of the video below.
A large piece of mass is placed in the center of the fabric. Viewed from above (Figure 9.6, left), it doesn’t seem like much has changed, but viewed from the side (Figure 9.6, right), we can see that the fabric is warped. This is similar to how largely massive objects: stars, planets, and so on, are able to curve spacetime.

Smaller objects can then be put in motion, and we can observe the effect of this spacetime warping, shown in the video above. Instead of traveling in straight lines like they did before, the marbles now travel in circular paths. This describes the orbits of planets around suns, and the orbits of moons and satellites around planets.
Further reading
- The Elegant Universe: Part 1 – Start watching the video at 9:52 to see the chapters of The Elegant Universe about squaring up Newton’s law of universal gravitation and what we know about the “universal speed limit” from Einstein’s theory of relativity.
Practice questions
Conceptual comprehension
- Make a list of scenarios (other than what’s provided in this textbook) where your apparent weight is either less than or greater than your gravitational force.
Numerical analysis
- Imagine a person standing on a bathroom scale inside an elevator. The elevator is accelerating upward at 2 m/s2. The magnitude of the person’s actual weight is 600 N. What is their apparent weight in the elevator?
- A roller coaster car goes through a loop-the-loop with a radius of 10 m. At the top of the loop, passengers experience a sensation of weightlessness. Calculate their apparent weight at the top of the loop if the coaster is moving at a speed of 20 m/s.
- Calculate the gravitational force between two 50 kg masses separated by a distance of 10 meters.
- Determine the gravitational force between the Earth and a satellite (with a mass of 200,000 kg) in orbit 500 km above the Earth’s surface. (Refer to Appendix B for information such as the mass of the Earth.)
- Calculate the magnitude of the gravitational force that the Sun exerts on Neptune (which has a mass of approximately 1 x 1026 kg). The Sun and Neptune are separated by a distance of 4.5 billion km. (Refer to Appendix B for information such as the mass of the Sun.)
- Calculate the gravitational acceleration on the surface of Jupiter. Jupiter has a mass of roughly 2 x 1027 kg and a radius of approximately 70,000 km.
- Calculate the gravitational acceleration on the surface of Venus. Venus has a mass of about 5 x 1024 kg and a radius of approximately 6,000 km.
- Calculate the gravitational acceleration on the surface of Saturn’s moon, Titan. Titan has a mass of roughly 1.3 x 1023 kg and a radius of approximately 2,600 km.
- A satellite orbits the Earth at an altitude of 400 km above the surface. Its centripetal force is supplied by its gravitational force with the Earth. Calculate the velocity of the satellite.
Hands-on experiments
- Drop various objects of different sizes and masses (make sure they are safe and won’t break) from the same height and use a stopwatch to time how long it takes for each object to reach the ground. Does the amount of time vary based on mass? Try to control for as many variables as you can.
- If you have a bathroom scale, bring it into an elevator and watch your apparent weight change as you accelerate upward or downward. (Is your apparent weight different from your unaccelerated weight when the elevator is moving at a constant velocity?)
The weight of an object is proportional to its mass as well as the force of gravity acting on that object, related by Newton's second law. More accurately, weight arises due to a supporting force acting on the object.
A force is a push or a pull that causes an object to change its motion. More fundamentally, force is an interaction between two objects. (symbol: F, unit: N)
Mass is a property of physical objects that relates to resistance to changes in motion: inertia. (symbol: m, unit: kg)
Gravity is the attractive force experienced by objects of mass. It is one of the four fundamental forces.
Apparent weight is equal to the value of the support force acting on a person. This causes our perception of having weight.
Acceleration quantifies the rate at which an object changes its velocity. (symbol: a, unit: m/s^2)
Speed is the scalar quantity that describes the rate at which an object changes its position. Speed is equal to position divided by time. (symbols: s, |v|, unit: m/s)
The net force is the vector sum of all forces acting on an object.
A vector quantity is a variable that must be conveyed with both a numerical quantity (indicating magnitude or strength) and a direction.
Free fall is defined as a situation where gravity is the only force acting on an object. Forces such as friction and air drag are ignored and assumed to be equal to zero. The acceleration of an object in free fall is defined by the acceleration due to gravity (g).
The orbit of a satellite describes its path around a planet or star.
Intensity describes the amount of energy per unit of area that reaches a certain location every second (unit: W/m^2)
Electric charge is a fundamental property of matter that causes particles that carry a charge to experience a force when in the presence of an electric field.
The center of mass is the point in an object (or system of objects) around which it rotates freely. It is considered to be the average position of all the mass in a system.
Density describes the compactness of matter in a substance, defined as the mass per unit volume. (symbol: D, unit: kg/m^3)
Centripetal force is a force, pointing toward the center of the rotational motion of an object, that causes an object to move in a circular path. (symbol: F_c, unit: N)
Path describes the total distance that an object travels as it moves from one point to another, measured along its trajectory. It is a scalar quantity. (symbols: d, x [for horizontal path], y [for vertical path], unit: m)
Newton's second law states that the acceleration of an object is proportional to the net force acting on the object, and inversely proportional to the mass of the object. In equation form, Newton's second law can be stated as F_net = ma.
A theory is an explanation of how the universe works that is supported by multiple, repeated experiments.

