13. Liquids
Summary
Pressure
Pressure is a concept that is important in solids, liquids, and gases. Even the pressure of the atmosphere plays an important role in our lives.
The symbol for pressure is the capital letter ![]() . The SI unit of pressure is the pascal (Pa), which can be broken down into N/m2. Pressure caused by a solid object is equal to force divided by area, or
. The SI unit of pressure is the pascal (Pa), which can be broken down into N/m2. Pressure caused by a solid object is equal to force divided by area, or
![]()
In other words, this is the amount of force divided by the amount of area over which the force is applied.
When Dr. Pasquale participated in the “bed of nails” demo, which was explained in chapter seven, the reason the nails don’t hurt her too much when she lies down on them is because the weight of her body, the force involved in the equation, is distributed over a large number of nails. While each nail has a relatively small surface area, the combined surface area of all of the nails causes the pressure to be less than it would be on any given nail. Dr. Pasquale would not have done this demo if there had only been one nail on the board!
Pressure is also a concept that is important in fluids: liquids and gases. In a liquid, the pressure is equal to the density of the liquid times the gravitational acceleration times the depth, in other words,
![]()
If you’ve ever gone swimming or scuba diving and had your ears pop, that’s because the pressure in water increases as you swim deeper and deeper. Note that the equation for pressure does not have to do with how large an area the liquid is distributed over: it only has to do with the density, gravitational acceleration, and depth. If you dive 5 meters under the surface of Lake Michigan, you would experience the same pressure that you would 5 meters under a freshwater pond, even though the two bodies of water are different sizes.
One of the consequences of liquid pressure is that water always “seeks its own level” in a container. If you’ve ever taken a container of liquid and tilted it, perhaps you’ve noticed that the water level will always even out. A video of this is shown below.
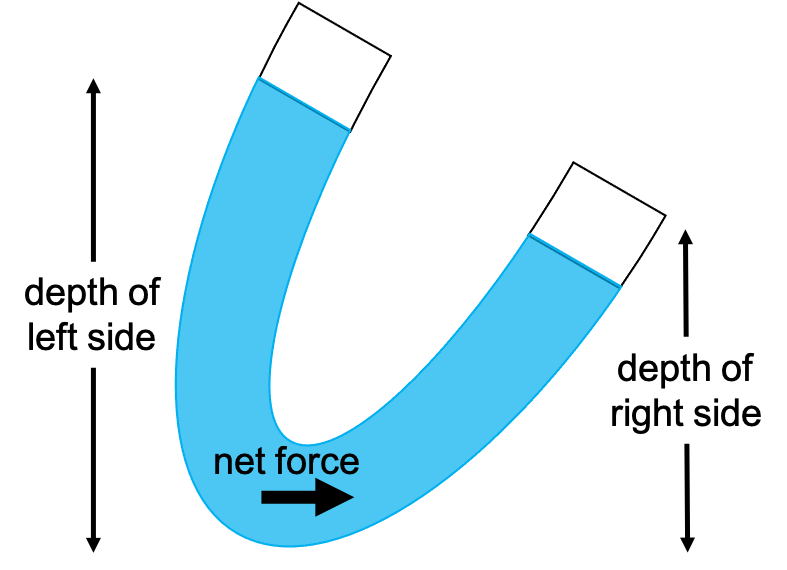
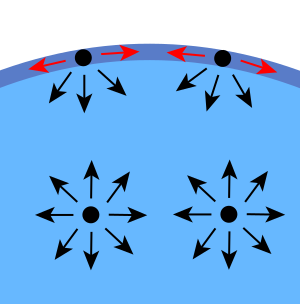
Even in the strangely shaped container shown in the video (and also shown in Figure 13.1), water seeks its own level as a result of keeping all forces due to water pressure in the fluid in equilibrium.

Consider an example of water that is not equalized after rotating a container, shown in Figure 13.2. The depth of the water is unequal from one end to the other. In the example shown in Figure 13.2, the left-hand side has a higher height above the bottom of the container, and the right-hand side has a lower height above the bottom. This causes more pressure to be present on the left. If there’s more pressure, then there is a net force between the left and right side. Newton’s laws state that when there’s a net force, there will be acceleration. The water will move until the height is equal on both sides, causing an equal amount of pressure on each side resulting in no net force.
Archimedes’ principle
If you’ve gone swimming, you may have noticed that you feel like you weigh less in water than you do on land. It’s true! Liquids exert an upward buoyant force on submerged objects, which means we exert less of a support force if we’re standing in a pool or other shallow body of water than we would if we were on dry land. If the density of a fluid is high enough, such as in salt water, the buoyant force may actually be large enough to reduce the support force to zero and cause us to float.
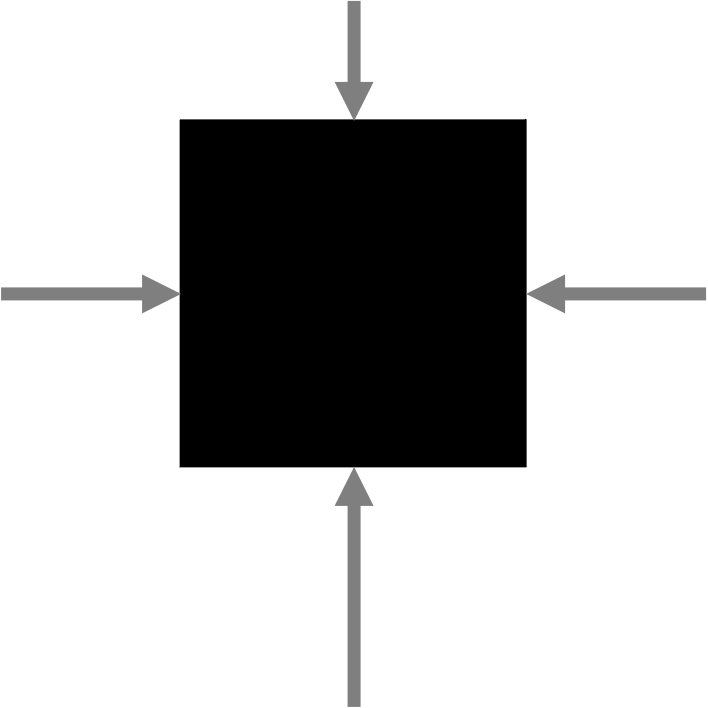
The buoyant force acting on an object placed in a liquid has to do with the differences in the fluid pressure between the top and bottom surfaces of the immersed object. For example, a cube placed in water is going to have pressure exerted on each of the faces of that cube, creating a force on each cube face (as depicted in Figure 13.3). Because pressure increases with depth, the lowest part of the cube has more force than the highest part of the cube because the greater pressure on the same sized area produces a greater force. All of the horizontal forces on the cube cancel out. The difference between the force pushing down on the top surface and the force pushing up on the bottom surface produces a net force pointing up. This difference is the buoyant force.
All objects placed in a liquid have a buoyant force pointing upward. If you place an object that sinks at the bottom of a container filled with water, that buoyant force will act on the object. When the object sinks, it stays put at the bottom of the container. There’s no net force. This means the gravitational force acting on the object (mass times gravitational acceleration) is canceled out by the buoyant force and support force. The forces acting on a lead weight that sinks in water are shown in Figure 13.4. The buoyant force causes the support force to be smaller than it would be on land. This is why we feel lighter in a swimming pool.

An object that floats will have a buoyant force greater than or equal to the gravitational force acting on the object. If an object that floats is fully submerged in water, the buoyant force, being greater than gravitational force, leads to a net force, causing the object to accelerate upward (see Figure 13.5, left). At some point the object will reach equilibrium as it rests on the surface of the water. The buoyant force decreases as the object displaces less liquid as it moves upward out of the water. When the gravitational and buoyant forces are equal, the object will stop moving and simply float (see Figure 13.5, right).

The wooden sphere from Figure 13.5, placed into the bottom of a tank of water, will experience a net force, causing the wooden sphere to accelerate upward until the forces are in equilibrium. This is shown in the video below.
Archimedes’ principle states that the buoyant force is equal to the weight of the fluid that is displaced when a solid object is placed into a fluid. This means that the buoyant force is equal to the mass of the displaced fluid times the gravitational acceleration. Since density is mass divided by volume, we can write the mass of the displaced fluid as equal to the density of the fluid times the volume of the displaced fluid. Therefore, the magnitude of the upward buoyant force can be written as the density of the fluid times the volume that is displaced times the gravitational acceleration. In other words,
![]()
Buoyant force, being a force, is measured with newtons (N). Recall that newtons are equal to kgm/s2. In order for units to work correctly in the buoyant force equation, the density of the fluid must be expressed in units of kg/m3 (not cm/g3). In addition, volume must be expressed in m3, not cm3. If you have different units for density or volume, then you must first do a unit conversion before determining the force in newtons.
The equation for buoyant force implies that for two objects in the same liquid, whichever object displaces the most liquid will experience the larger buoyant force. If both objects displace the same amount of liquid, then they will experience the same magnitude of buoyant force.
A second equation that can be used to quantify buoyant force is that the buoyant force on an object is equal to the weight of the object in air minus the weight of the object in the fluid. In other words,
![]()
Shown in the video below is another demonstration of Archimedes’ principle. Dr. Pasquale has a heavy brass ball sitting on some dried beans. When she shakes the container, the brass ball moves downward to the bottom of the container, and out pops a ping-pong ball! The ping-pong ball has a lower density than the dried beans, and therefore experiences a buoyant force. The brass ball has a high density and sinks. This demonstration only works when Dr. Pasquale shakes the container, creating a type of fluid flow.
Flotation
The principle of flotation states that any object that floats displaces a weight of fluid equal to its own weight. For example, a boat that has a weight of 10,000 N will float if it displaces 10,000 N of water.
A solid piece of iron has a density approximately 8 times greater than that of water. This means that if we were to place a piece of solid iron into a container of water, it would only displace one eighth of its weight in water. This is not enough to make it float.
If iron sinks in water, how is it that boats and submarines can be made out of iron and other dense metals? If you think about the shape of a boat in a simplistic manner, it is carved out so that it is able to displace its own weight in water. Effectively, the boat has sections of air that cause the overall density of the submerged portion of the boat including the air to be less than that of the fluid on which it is floating.
An object that is less dense than a fluid will float in that fluid. An object that is more dense than a fluid will sink in that fluid.
Pascal’s principle
Pascal’s principle states that a pressure change everywhere in a closed system of a liquid is equal at all points in the system.
In equation form, Pascal’s principle states that
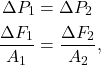
where ![]() and
and ![]() are pressure changes at two points in a closed system. If a force is applied to point 1,
are pressure changes at two points in a closed system. If a force is applied to point 1, ![]() is the force applied at that point and
is the force applied at that point and ![]() is the area over which the force is applied. At point 2, having an area of
is the area over which the force is applied. At point 2, having an area of ![]() ,
, ![]() is the output force. In other words: the change in force divided by the area at one point in a system equals the change in force divided by area somewhere else in the system.
is the output force. In other words: the change in force divided by the area at one point in a system equals the change in force divided by area somewhere else in the system.
This equation is depicted in Figure 13.6. A closed system of fluid containing two pistons (one small, left, and one large, right) shows the relative forces that would be present on each piston to abide by Pascal’s principle. Because the piston on the left is small, a small force applied at that point would yield a large force on the large piston (on the right).
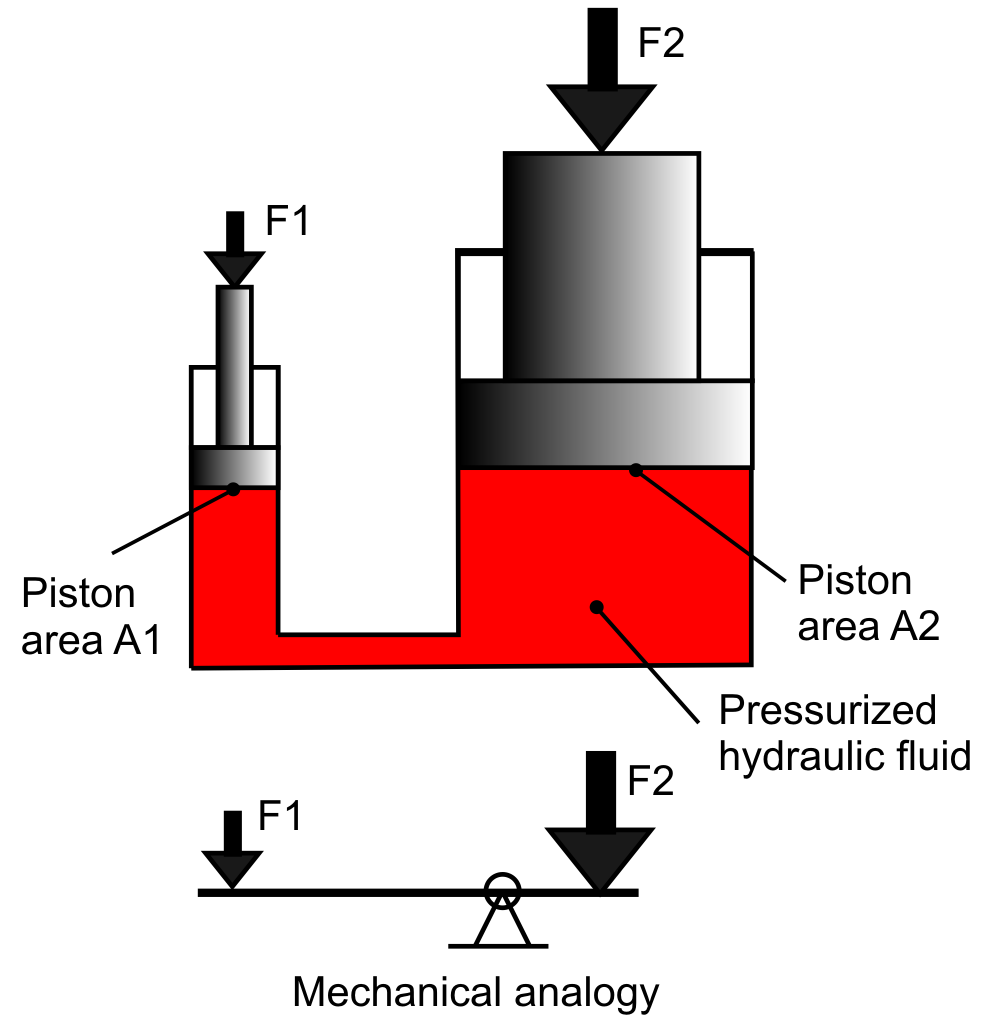
In Figure 13.6, a mechanical analogy is also shown, as this is similar to the mechanical advantage that can be obtained with a lever (which is a type of simple machine). This is because the volume of fluid pushed out of the small piston is equal to the volume of fluid pushed into the large piston (due to conservation of mass). Because volume equals cross-sectional area times height, the small piston moves a small force through a long distance (height) while the large piston moves a large force through a short distance.
In the video below, Dr. Pasquale has a piston system similar to that shown in Figure 13.6. When she places a mass of 200 g on the smaller piston (on the right), that generates a force of 2 N due to gravity. That force is exerted over a small area, causing a pressure change. As a result, an equal pressure change will occur over the large piston. This results in a mass of 500 g (with a weight of 5 N) lifting up. The force that Dr. Pasquale placed on the small piston was multiplied by 2.5 due to the mechanical advantage provided by Pascal’s principle.
This mechanical advantage forms the basis of hydraulic systems. A small force can be exerted on a small area to achieve a large force output on a large area somewhere else. If the mechanical advantage is large enough, this could be used to lift something really large, like a car. Hydraulic lifters use this principle to lift heavy objects. Hydraulics are also used in automobile braking systems. Exerting a small force on a pedal causes our cars to slow down. Hydraulics are also used in large airplanes. Pilots can exert a small force on a control yoke or rudder pedals and a hydraulic system creates a deflection in the airplane flight controls that would otherwise be too heavy for humans to move on their own.
Pascal’s principle also forms the foundation for modern water supplies and distribution systems. In the Midwest where it’s relatively flat, we have water towers to create water pressure. A photograph of a water tower in Naperville, IL is shown in Figure 13.7. When you open the tap on a sink, there will be water pressure because the building is connected to a water main that’s pressurized.

The bad news is that if there is a break in the water main at any point, water pressure will be lost everywhere in the water system. When author Dr. Pasquale was living in Boston in 2010, there was a water main break that caused about two million people, including her, to lose water pressure in their homes and apartments. Because the pressure change is transmitted throughout a system, a water break in one spot will transmit everywhere!
Surface tension
Surface tension is a force that acts parallel to a surface of liquid, such as water. This is depicted in Figure 13.8. As a result of surface tension, liquids such as water will tend to minimize their total surface area to minimize the forces acting on each molecule. In short, surface tension describes the resistance of the surface of a liquid to being stretched.
In most liquids, including water, surface tension causes water to form drops. The spherical shape of the drop minimizes the amount of force present on the surface. In a way, you can think of the spherical shape as the most comfortable arrangement for the molecules. A photograph of a water droplet falling out of a pipette is shown in Figure 13.9 (in fact, even the water stuck to the sides of the pipette is spherical or dome-shaped).
In a volume of water, bonds between molecules will cause the molecules in the center of the water to have no net force. Molecules at the surface don’t have forces acting on them in all directions, causing a force of surface tension.

Surface tension explains how objects with enough surface area can rest on the top of water without getting submerged. In Figure 13.10, a paper clip is shown resting at the top of a beaker of water. The paper clip is not floating. Aluminum is more dense than water, so we would expect it to sink. However, the paper clip is sitting on top of the water because the surface tension of the water is greater than the weight of the paper clip. Much like the surface of a trampoline, the surface of the water stretches and sags slightly due to the weight of the paper clip resting on top of it.

In the video below, Dr. Pasquale places the paper clip into the beaker of water. When she pushes down on the paper clip, the downward force is large enough to break through the surface tension. The object “falls through” the surface. (In our trampoline analogy, the trampoline’s surface has been torn.) The paper clip then sinks as expected, since the aluminum is more dense than water.
Similar to the paper clip resting on top of water, insects like water striders can walk across water. Surface tension also explains why it hurts to do belly flops into a swimming pool: when your body must break through the force of surface tension, it can be painful!
Capillarity
Capillarity is related to surface tension. When liquids are in a narrow space, they can cause the surface of a liquid to form a curve called a meniscus. If in a narrow enough space, the liquid can rise up the walls of a container. The curvature of the meniscus depends on the competing effects of cohesion versus adhesion. Atoms and molecules attract to other atoms and molecules through electrical interactions of their electrons. The attractive forces between “like” atoms and molecules (such as water molecules to other water molecules) is referred to as cohesion. The attractive forces between “unlike” atoms and molecules (such as between mercury and glass) is referred to as adhesion. Referring to Figure 13.11 (right), the adhesive force between water and glass is greater than water’s cohesive force. In other words, water would rather stick to the glass than next to other water molecules. This arrangement creates a concave meniscus shape as water molecules are drawn up along the glass. This minimizes the forces in the water. In the case of mercury in glass (shown in Figure 13.11, left), the mercury atoms would rather stick to themselves than stick to the glass. This results in a convex meniscus that is opposite to the water-in-glass meniscus as the mercury atoms clump together as much as possible.

Capillarity explains how paper towels absorb moisture, how trees get water from their roots to their branches, and how small amounts of blood can be drawn using a finger stick.
Practice questions
Conceptual comprehension
- Which of the two spheres shown in Figure 13.12 experiences the larger buoyant force, the wooden sphere (floating, left) or the iron sphere (sinking, right)? Both spheres have identical volumes.

Numerical analysis
- A heavy box with a mass of 30 kilograms is placed on the floor. If the box has a base with dimensions of 0.5 meters by 0.5 meters, calculate the pressure that the box exerts on the floor.
- The book shown in Figure 13.13 has a thickness of 4.5 cm, a depth of 20.5 cm, and a height of 26 cm. It weighs 22 N. Calculate the pressure exerted by the book on the table when it is…
- …upright (Figure 13.13, left).
- …laying down (Figure 13.13, right).

- A person weighing 550 N has a foot area of 160 cm2 each. Sometimes this person enjoys wearing high heels, which have an area of 1 cm2 each. Calculate the pressure the person exerts on the floor when they are…
- …barefoot.
- …wearing high heels. (Assume the person is balanced with all of their weight on the heels of their feet in this scenario.)
- A car with a mass of 1,200 kg has tires with an area of contact with the road of 0.02 m2 each. Calculate the total pressure exerted by all four tires on the road when the car is stationary.
- A freshwater swimming pool is 2 meters deep. Calculate the pressure at the bottom of the pool due to the weight of the water.
- A submarine is 30 meters below the surface of the ocean. Calculate the pressure exerted on the submarine due to the weight of the water above it. (Assume the density of seawater is 1,025 kg/m3.)
- A solid metal cube with a volume of 0.02 m3 is completely submerged in freshwater. If the density of the metal is 8,000 kg/m3, what is the buoyant force acting on the cube?
- A wooden block with a volume of 0.05 m3 and a density of 600 kg/m3 is placed in a container of oil with a density of 900 kg/m3. Calculate the buoyant force on the wooden block when it is fully submerged in the oil.
- A ship has a mass of 400,000 kg. Calculate…
- …the weight of the ship.
- …the weight of liquid that must be displaced to cause the ship to float.
- …the volume of freshwater that must be displaced to cause the ship to float.
- …the volume of seawater (1,020 kg/m3) that must be displaced to cause the ship to float.
- If a force of 200 N is applied to a piston with an area of 0.02 m2 in a hydraulic system, calculate the pressure that is exerted on the fluid inside the system.
- In a hydraulic jack, the small piston has an area of 0.005 m2, and the large piston has an area of 0.05 m2. If a force of 500 N is applied to the small piston, calculate the force that will be exerted by the large piston.
- In a hydraulic lift used to raise a car, the small piston has an area of 0.02 m2. If a force of 10,000 N is applied to the small piston, calculate the force that will be exerted on the car resting on the larger piston (with an area of 0.1 m2).
Hands-on experiments
- You can demonstrate density by making a simple density tower using liquids of different densities, such as water, vegetable oil, and syrup. Pour these liquids carefully, one on top of the other, in a clear container. Objects (like raisins or small plastic toys) can be added to see if they float or sink, depending on their density relative to the surrounding liquid.
Pressure defines the amount of force applied over an area of a substance. (symbol: P, unit: Pa)
A solid is a substance where the molecules or atoms are very tightly bound together. This gives a solid a very rigid volume and shape. Solid is one of the four most common phases of matter.
A liquid is a state of matter in which the constituent molecules will change their shape or arrangement but cannot be easily compressed to change their volume. Liquid is one of the four most common phases of matter.
Gas is a state of matter where molecules are very free to move about and generally do not interact with each other except during collisions. This means that the shape and volume of a gas is free to change. Gas is one of the four most common phases of matter.
A force is a push or a pull that causes an object to change its motion. More fundamentally, force is an interaction between two objects. (symbol: F, unit: N)
The weight of an object is proportional to its mass as well as the force of gravity acting on that object, related by Newton's second law. More accurately, weight arises due to a supporting force acting on the object.
Density describes the compactness of matter in a substance, defined as the mass per unit volume. (symbol: D, unit: kg/m^3)
The net force is the vector sum of all forces acting on an object.
Acceleration quantifies the rate at which an object changes its velocity. (symbol: a, unit: m/s^2)
Mass is a property of physical objects that relates to resistance to changes in motion: inertia. (symbol: m, unit: kg)
Archimedes’ principle states that the buoyant force that acts on a substance is equal to the weight of the fluid that is displaced when that substance is placed into a fluid.
The principle of flotation states that any object that floats displaces a weight of fluid equal to its own weight.
A system is any collection of objects that we define. The concept of a system is used to determine what is internal or external when discussing concepts such as momentum conservation.
Mechanical advantage is a force multiplication that can be provided by a simple machine. (symbol: MA, unit: none)
A simple machine is used to change either the direction or magnitude (or both) of an applied force. There are six types of simple machines: levers, wheels and axles, pulleys, inclined planes, wedges, and screws.
Gravity is the attractive force experienced by objects of mass. It is one of the four fundamental forces.
An electron is a fundamental building block of matter that has a negative charge and is found surrounding the nucleus of an atom.

