4. Newton’s second law

Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; Carley Bennett, Ph.D.

4. Newton’s second law

Summary

Newton’s second law of motion describes the relationship between force, mass, and acceleration. This will expand upon our current understanding of motion, and open us up to discussions about momentum, energy, and more in the next several chapters.

Force

Simply put, a force is some type of push or pull that causes an object to change its motion. The symbol for force is the capital letter $\vec{F}$ . The unit for force is the newton (N).

There are many manifestations of forces. These include gravity, support force, friction, viscous drag, applied forces, tension, elastic/spring forces, electrical, magnetic, and nuclear forces.

Gravity

Gravity is one of the most prevalent forces in our lives. At this stage, it will suffice to say that gravity is a force of attraction between masses. Because the Earth has an enormously large mass, it creates a large attractive force, causing us to constantly experience a downward force pulling us toward the center of the Earth.

If you’ve ever dropped something, or rolled something downhill or down a ramp, then you’ve seen gravity’s effect on the motion of an object. In addition, our weight comes from gravity.

Support force

A support force occurs whenever something is in contact with a surface such as the ground, the floor, a wall, or something else. If you are standing as you read this, then the floor is supporting your weight and preventing gravity from accelerating you to the center of the Earth. The support force is sometimes called a normal force as the force always acts perpendicular to the supporting object. (In science and mathematics, the term “normal” means “perpendicular.”)

When an object is in contact with a flat surface, the normal force will point up. But when that surface is tilted, then the normal force no longer points up. It points perpendicular to the surface. This is shown in Figure 4.1.

Two photographs are displayed side-to-side. The left photograph shows a wooden block sitting stationary on a horizontal metal track. An annotated arrow directly over the block points upwards and depicts the support force. In the background is a black curtain. The right photograph shows the same wooden block sitting stationary on a track that tilts downward and to the right. A jack stand can be seen holding the track upward on one side of the track. An annotated arrow directly over the block points upwards and to the right and depicts the support force. In the background is a black curtain. — Figure 4.1 – The support force vector points up when an object is on a horizontal surface (left), and has an angle perpendicular to any tilted surface (right). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Friction

Friction is another force we experience in our daily lives. There are two types of friction: static friction and kinetic friction.

Static friction

Static friction is the force that must be overcome in order to get an object at rest to start moving. When static friction is involved, the surfaces in contact do not slide past one another. For example, if you’ve ever tried to move something heavy by pushing it, perhaps you’ve noticed that it takes more effort to get the object to start moving than it takes to get it to continue moving. That’s because of static friction. Static friction is also the force we experience between our feet and the ground when we walk or run. It is also the force between wheels and pavement when we drive a car, ride a bicycle, or push a wheelchair.

Kinetic friction

Kinetic friction is the force that occurs between surfaces as they slide past each other. The amount of kinetic friction depends on the two materials that are in contact with each other as they slide. Something like steel and ice will experience relatively low kinetic friction, which you may have experienced if you’ve ever gone ice skating. On the other hand, wood and steel would experience much more kinetic friction.

Another factor that influences the amount of kinetic friction is the support force between the object and the surface that it slides along. The larger the support force, the higher the kinetic friction, all other things being equal. Interestingly, for dry non-lubricated surfaces, the force of friction is essentially independent of the relative speed of the sliding surfaces.

Viscous drag

Viscous drag is a force that occurs when an object travels through a fluid, such as air or water. Drag acts in the opposite direction of motion. Consider an object tossed into the air. When the object is moving up, the drag (air resistance) will point down. When the object is moving down, the air resistance will point up. Unlike friction, air resistance does depend on the speed of an object. The faster the object goes, the greater the air resistance will be.

An entire area of study, aerodynamics, has been created to determine what kinds of objects travel through the air without experiencing too much drag. You can get an idea about aerodynamic shapes by looking at airplane design, especially fast airplanes that would otherwise be subject to very high resistance at their speeds. In the case of airplanes and other aircraft, air resistance is something that needs to be minimized to keep the fuel costs of air travel as low as possible.

Air resistance will reduce the acceleration of an object traveling through the air. Consider a rock dropped from the top of a tall skyscraper. If that rock falls only under the influence of gravity, then its speed will increase linearly over time as gravity increases its speed by 9.8 m/s every second.

However, air resistance will act on the rock to reduce the rate at which the speed increases. At first, when the rock is initially dropped, air resistance will be zero because the rock is not moving yet. As the rock speeds up, the air resistance will increase. This limits the increase in speed. At a certain point, air resistance and gravity will become equal to each other, causing the object to fall at a constant speed. This speed is known as the terminal speed. The rock will continue moving at its terminal speed until it hits the ground. The velocity vs. time graph for each scenario (with and without air drag) is shown in Figure 4.2. (Download this data [XLSX, 9 kB])

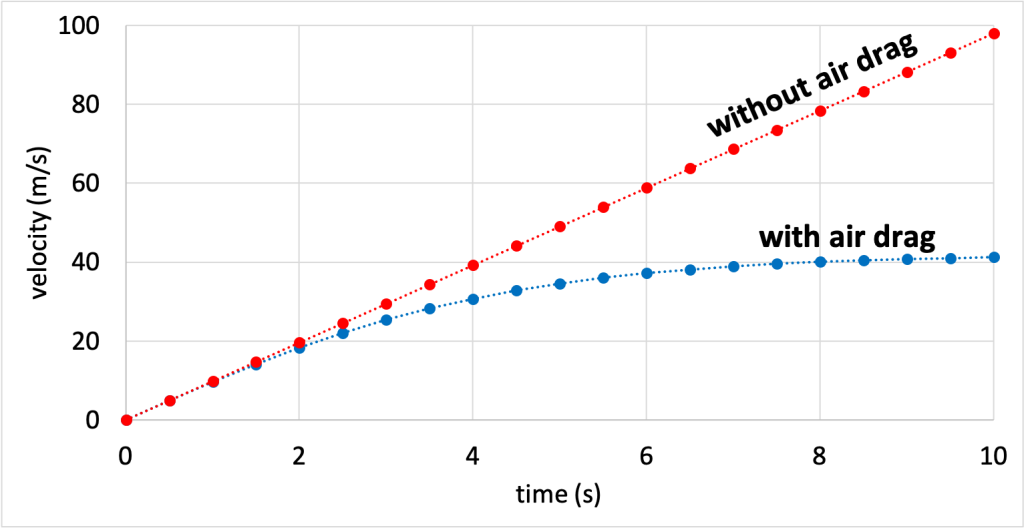
A graph has velocity (m/s) plotted on the y-axis and time (s) plotted on the x-axis. There are data points plotted for an object falling without air drag, with a linear fit line demonstrating the relationship between velocity and time. This data increases linearly from (0,0) to (10,100). There are data points plotted for an object falling with air drag, with a non-linear fit line demonstrating the relationship between velocity and time. This trend appears to rise linearly for the first two seconds, then rise until asymptotically getting to approximately 40 m/s at around 8 seconds, where the data then remains constant. — Figure 4.2 – A velocity vs. time graph for a rock falling both with and without air drag. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Every object will have a different terminal speed depending on its size, shape, density, and other factors. If we drop any object from a large enough height, it will speed up to its terminal speed, and then travel in dynamic equilibrium at that terminal speed until it hits the ground.

Air resistance is not always a bad thing. We can use air resistance to make falls from great heights not only survivable, but also fun. Skydivers use parachutes to decrease their terminal speed and allow them to survive after jumping out of an airplane.

Objects moving through the vacuum of space will not experience any air resistance. This is because there is no fluid such as air to act on the object to change its motion. This concept was demonstrated in 1971 on the Apollo 15 mission by astronaut Dave Scott. He dropped a hammer and a feather at the same time, and because there is no atmosphere on the Moon, there was no air resistance that would cause the feather to move slower than the hammer. Both objects hit the surface of the Moon at the same time.

Applied force

An applied force is simply a push or pull that is applied to an object by an outside influence. Whenever we move an object by pushing or pulling, we are applying a force. For example, if you push a car stuck in the snow or pull a child in a sled, you are applying a force. The magnitude and direction of that force depends on how hard and which way you push or pull.

Tension

Tension is the pulling force present in a string, cable, or other object as it holds something up. The direction of the tension force is along the string or cable. Tension is present in pendulums, pulley systems, and even in truss bridges.

Elastic and spring forces

Elasticity describes how much an object deforms when experiencing a stress or force. Springs are a great example of an object that can be deformed with a force. After the force is removed, as long as the force wasn’t too large, the spring will restore itself to its original size and shape.

Electromagnetic force

Electromagnetism describes the interactions of charged objects and magnetic materials. In our daily lives, we experience electromagnetism any time we use an electronic appliance or gadget, and even when we do something as mundane as use a magnet to hang something on a refrigerator.

Nuclear forces: the strong and weak forces

The strong and weak nuclear forces are forces present inside the nucleus of an atom. They’re not forces we think about in our daily lives, and yet they are important in that they literally keep atoms together. Electromagnetism tells us that objects with like charges repel. So what is it that keeps the nucleus of an atom, comprised of like-charged protons, together? The answer is the strong force. The strong force acts on a very small scale to keep the nucleus of an atom together. It also helps us to understand nuclear processes such as fission and fusion.

The weak force is responsible for radioactive decay. It is the force responsible for changing one type of quark into another, say, by turning a proton into a neutron.

Fundamental forces

While there are many different forces that can act on an object, there are only four fundamental forces. That is to say, all of the forces just described can be put into one of four categories. Those categories are gravity, electromagnetism, the strong force, and the weak force.

Pretty much all of the forces that we experience in our lives, other than gravity, actually fall into the category of electromagnetic forces. The support force, for example, occurs due to the repulsion of electrons in two atoms when they are placed near each other. Friction occurs due to electromagnetic forces interacting at the surfaces of two objects that are touching each other. And so on.

type of force	fundamental force type
gravity	gravity
support force	electromagnetism
friction	electromagnetism
viscous drag	electromagnetism
applied force	electromagnetism
tension	electromagnetism
elastic and spring forces	electromagnetism
electromagnetic forces	electromagnetism
the strong force	strong force
the weak force	weak force

Of the four fundamental forces, the strongest is the strong force, followed by electromagnetism, the weak force, and gravity. Gravity is by far the weakest of the four fundamental forces.

Newton’s second law

Acceleration defines the rate at which the velocity of an object changes. Acceleration can mean one of three things: that an object is speeding up, slowing down, or changing direction. Newton’s second law defines the relationship between force, mass, and acceleration.

Newton’s second law states that the net force on an object is equal to its mass times the acceleration. In other words,

$\vec{F}_{net} = m\vec{a}.$

The net force is the sum of all of the forces that act on an object, and it is a vector quantity. Acceleration is also a vector, and it will point in the same direction as the net force. Newton’s second law can be rearranged to solve for acceleration, in which case

$\vec{a} = \frac{\vec{F}_{net}}{m}.$

Mechanical equilibrium occurs when the net force on an object is equal to zero. If the net force is zero, we can see from Newton’s second law that the acceleration is also zero.

Consider pushing on a very heavy box to try to get it to move. As you push on the box, the box does not move. Friction is the force acting against your push, but how could we calculate the magnitude of that force? Is friction greater than, less than, or equal to the push?

We can use Newton’s second law to find an answer. Let’s say you push against the box with a force of 25 N, and the box does not move. Because the box is not moving, it is in static equilibrium (velocity is constant at zero and acceleration is equal to zero). We know from Newton’s second law that the net force on the box must be zero. We can express the net force on the object as

$\vec{F}_{net} = \vec{F}_{applied} + \vec{F}_{friction},$

where $\vec{F}_{net}$ is the net force, $\vec{F}_{applied}$ is the applied force, and $\vec{F}_{friction}$ is the friction force. The sum of these three vectors is zero.

We can plug in 25 N for the applied force, and solve for the force of friction.

$\begin{align*} \vec{F}_{net} = 0 &= 25~\textrm{N} + \vec{F}_{friction}\\ -25~\textrm{N} &= \vec{F}_{friction} \end{align*}$

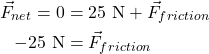
This calculation states that friction is equal to -25 N. The negative sign indicates that it points in the opposite direction as the applied force. But the applied force and friction have equal magnitudes: 25 N!

Students frequently have a hard time with this concept. If you struggle with the idea that friction and the applied force are equal when the box is not moving, then consider an extreme example. Consider what would happen if the force of friction could somehow be greater than your applied force. In this case, as you push against an unmoving box, if friction somehow became larger than your applied force, it would cause a net force in the direction opposite of your push, causing the box to accelerate against the direction of your push! That’s definitely not what happens when you push on an object.

This situation (applied force and friction forces are equal in magnitude but opposite in direction) is the same once you get the box moving at a constant speed. Once the box is moving at a constant velocity, the box is in dynamic equilibrium, and the net force is again equal to zero. As long as there are no other forces acting on the box, the force of friction must be equal and opposite to your push.

Consider a two-dimensional example. A cart moves down an inclined track, speeding up as it moves. Ignoring air drag, there are three main forces acting on the cart: friction (which points in the direction opposing motion), a support force from the track (which points perpendicular to the track), and gravity (which points toward the center of the Earth). These vectors are qualitatively shown in Figure 4.3, left.

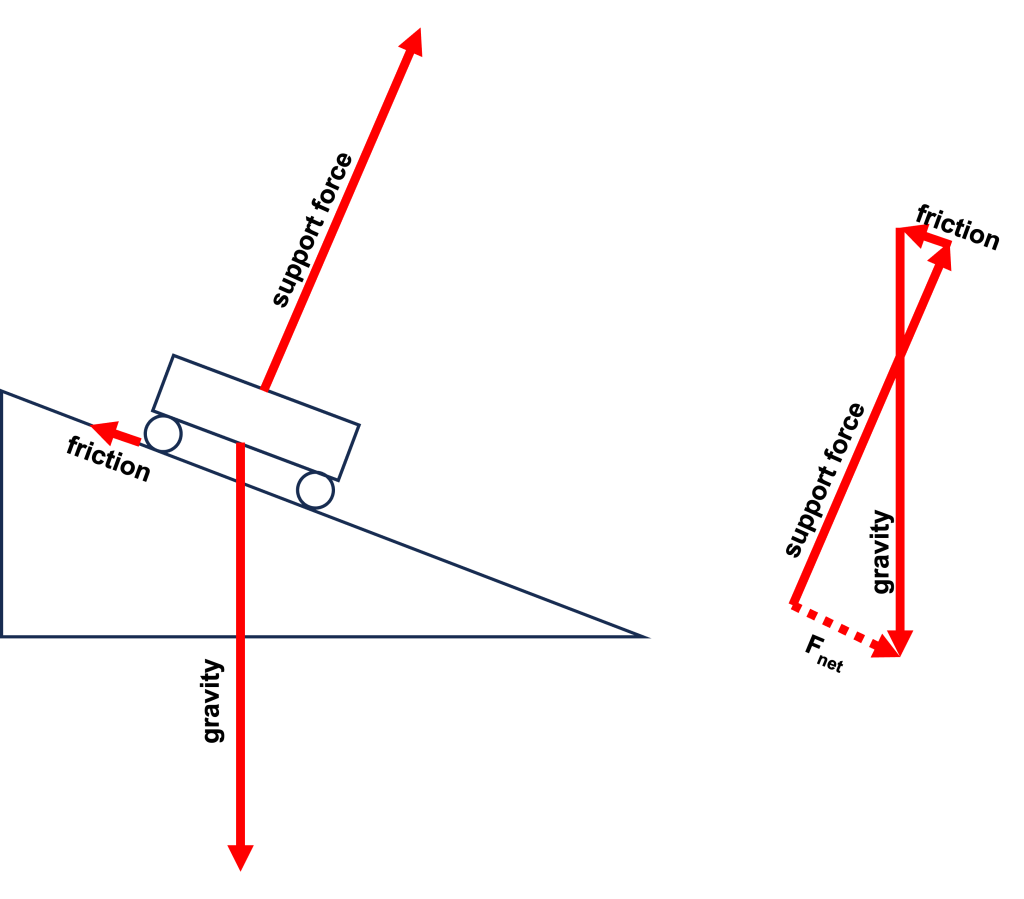
Figure 4.3, described in the text. — Figure 4.3 – A cartoon cart is depicted as rolling down a triangular ramp. The support, friction, and gravity force vectors are drawn. (left) A graphical sum of the three force vectors leads to the resultant net force vector (right). This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

The force vectors can be added graphically, shown in Figure 4.3, right. The resultant vector shows the net force, which points down and to the right. This is in the same direction as the cart’s acceleration vector.

Mass and weight

It is important to review the concepts of mass and weight and how they differ from each other. This is another concept that is misused frequently, as people tend to (incorrectly, from a physics standpoint) use the terms interchangeably in casual conversation.

Mass comes from the “stuff” in an object: the atoms and molecules that it is made out of. Mass gives an object inertia, a resistance to changes in its motion. Because mass comes from the molecular configuration of something, it does not change based on position or location. While the situation for humans is admittedly complicated due to the fact that we eat, excrete, and exercise, if we could somehow hold our masses constant, that mass would not change if we were to be here on Earth, on the Moon, on Saturn, or just floating in the vacuum of space.

Weight, on the other hand, is a force that comes about due to the force of gravity. While weight is a somewhat complicated topic, for now it is sufficient to say that weight is equal to our mass times the acceleration we experience due to gravity, “little g”. In other words, $\vec{W} = m\vec{g}$ . “Little g” is equal to -9.8 m/s².

If we were to change our location, our mass would stay the same, but our weight might change. The gravitational force on the Moon is one sixth that of Earth. Therefore, our weight on the Moon will be one sixth the value of our weight on Earth. Astronauts visiting the Moon experienced this decreased weight as they conducted moonwalks.

Jupiter, however, has a much higher gravitational force than the Earth. If we could go to Jupiter (which actually has no solid surface upon which we could stand), we would find ourselves weighing 2.5 times more than we weigh on Earth. Meanwhile, if we could somehow safely transport ourselves to the Sun, the gigantic gravitational attraction of the Sun would make us weigh nearly 30 times our weight on Earth!

When astronauts visit the space station, or otherwise orbit the Earth, the lack of a support force causes them to be weightless. They are still under the influence of Earth’s gravity, which is what causes the space station to orbit the planet, but the astronauts and other objects traveling in orbit appear to be weightless. However, that does not mean that inertia has stopped impacting the motion of an object. Mass, and inertia, exist everywhere.

There is a NASA podcast episode that takes a fascinating look at the impact of inertia in space. Even when astronauts and their bulky equipment are weightless, the inertia of the objects still affects their ability to move around, put on their spacesuits, and get things done in space. NASA’s spacesuit hardware manager Les Padilla describes the effect of inertia in microgravity (this quote is recorded between times 30:37 and 31:04 in the podcast):

What can be our friend at times is momentum or inertia. That can be an enemy at times as well when you’re in that microenvironment. Crew members are trained specifically to go slow along a space station. If you get 300 pounds moving, it can be difficult to stop. Now, they can stop it, but it’s just wasted energy. So they go very slowly so they don’t get that large mass moving too quickly.

Practice questions

Conceptual comprehension

A small steel BB is inserted into coiled plastic tubing, as shown in Figure 4.4. It travels in several circles before exiting the tubing. What direction will the BB travel when it exits the tubing? Consider all of the forces acting on the BB at the time it exits the tube.

A piece of clear tubing is coiled up into loops. A hand is holding up the top of the tube to place a BB inside. — Figure 4.4 – A BB traveling through coiled tube will travel in a circular path while it’s moving through the tubing. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Numerical analysis

If an object with a mass of 5 kg experiences an acceleration of 2 m/s², calculate the net force that must be acting on that object.
Calculate the acceleration that will be created by a net force of 0.2 N acting on an object with a mass of 10 g.
Calculate the net force acting on a 10 kg bicycle moving at a constant velocity of 6 m/s.
A spacecraft (with a mass of 2 million kg) is in deep space, far from any significant gravitational forces, and is subject to two thrusting forces: a “horizontal” force of 2,000 N and a “vertical” force of 1,000 N. (The designations of “horizontal” and “vertical” are arbitrary; what is important is that the two forces act at right angles to each other.) Calculate the net force acting on the spacecraft. Then, calculate the acceleration of the spacecraft while the thrusters are in operation.
If an object on the surface of the Earth has a mass of 10 kg, calculate the gravitational force acting on that object.
On the Moon, the acceleration due to gravity is approximately 1.6 m/s². Calculate the gravitational force (weight) of a person who has a mass of 70 kg if they are on the Moon.

Hands-on experiments

Take two sheets of otherwise identical paper. Hold one of them so that it is flat and parallel to the ground. Crumple the second sheet of paper and hold it up to the same height as the flat paper. Drop both pieces of paper simultaneously. Which sheet of paper experiences more air resistance? How do you know?
Using household items, how can you demonstrate that the electromagnetic force is stronger than gravity?

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.