5. Newton’s third law

Newton’s third law

Newton’s third law states that for every action, there is an equal and opposite reaction. Forces always come in pairs: action-reaction pairs. As you read this book, you may be standing or sitting. You are pushing down on the floor (or ground). The reaction force is that the floor (or ground) is pushing up on you. How do you know the floor pushes up on you? It’s possible that you feel that force on your feet (if you are standing), or your thighs (if you are sitting), or your side (if you are laying down).

Any time two objects interact with each other, or exert forces on each other, there will be two forces: an action force and a reaction force. The two forces are equal in magnitude and opposite in direction. Also note that action-reaction pairs of forces never act on the same object.

If you high five somebody, there’s an action-reaction pair. Both hands exert equal forces on each other in opposite directions.

In sports, if you hit a ball with a bat, your head, your feet, or another object, there’s an action-reaction pair. Does it really matter which force we call the action and which is the reaction? Not really. In softball and baseball, the bat and ball both have equal forces exerted in opposite directions on each other. The bat exerts a force on the ball. By Newton’s third law, the ball exerts an equal and opposite force on the bat. Each represents forces on different objects (in this example, the ball and the bat).

Newton’s third law is applicable not only when two objects are stationary, but also when one or both of the objects is moving or even accelerating. In the video below, a force-sensing probe has been connected to a stand to hold it stationary. It is connected to a second force-sensing probe with a rubber band, which Dr. Pasquale pushes and pulls to create action-reaction pairs. The forces of each probe are recorded in real time using Logger Pro, and shown on the computer readout in the background of the video, demonstrating equal and opposite forces.

Dr. Pasquale then repeats the demonstration while holding both force probes, causing one or both of the force probes to be in motion at different times. This is shown in the video below. Regardless of whether the system is stationary, accelerating in one direction, or moving at a constant velocity, the two force probes exert equal and opposite forces on each other (shown on the computer readout in the background of the video).

Any time two objects are in contact with each other, they will exert equal and opposite forces, regardless of the mass, volume, speed, or acceleration of either of the objects.

As shown in Figure 5.1, a wheelchair user walking a dog experiences many action-reaction forces. The dog exerts a force on the leash to the right and the leash exerts the same-sized force on the dog to the left. This means there will be an interaction between the person and the leash: the leash exerts force on the person to the right. If we let this be the “action,” then the reaction force is the person exerting a force on the leash to the left. Other action-reaction pairs include:

• the person pushes down against the wheelchair, the wheelchair pushes up on the person,
• the wheelchair pushes down on the ground, the ground pushes up on the wheelchair,
• the Earth pulls down on the person, the person pulls up on the Earth, and
• the dog pushes on the ground to the left, the ground pushes on the dog to the right.

Tug of war

Consider the game of tug of war. In this game, two teams stand at opposite sides of a rope. Both teams pull on the rope, attempting to pull the other team over to their side. Both teams are in contact with the rope. (See Figure 5.2, below.)

If one team consists of lots of very muscular individuals, and the other team consists of just a few rather small individuals, which team exerts more force on the rope? The large group of large folks? The small group of small folks?

The answer is: both teams are exerting exactly the same force on the rope! How do we know this is true? If both teams are in contact with the rope, then Newton’s third law tells us that their forces will be equal and opposite. This is exactly the same situation we saw with the dog and the person walking the dog, as well as with the two force probes pulling against each other.

So who wins the game of tug of war? The answer is: whichever team exerts the most force on the ground with their feet will win the game. Why? The answer is that the team that pushes harder on the ground (toward the other team) will have the ground exert an equal force back on that team in the opposite direction away from the other team. If the team of very large people is standing on a slick floor wearing socks, they will not be able to exert a lot of force on the ground, and will be moved around very easily. If the team of very small people are standing on asphalt wearing rubber soled shoes, they will be able to exert a lot of force on the ground, and will be harder to move.

Next time you play a game of tug of war, wear shoes that give you a lot of traction with the floor, and make good contact. Note the footwear and position of the schoolchildren playing tug of war in Figure 5.2, indicating the importance of the force against the ground in winning the game. It doesn’t matter how hard you pull on the rope, as long as your feet exert a larger force on the ground than your opponents’ do!

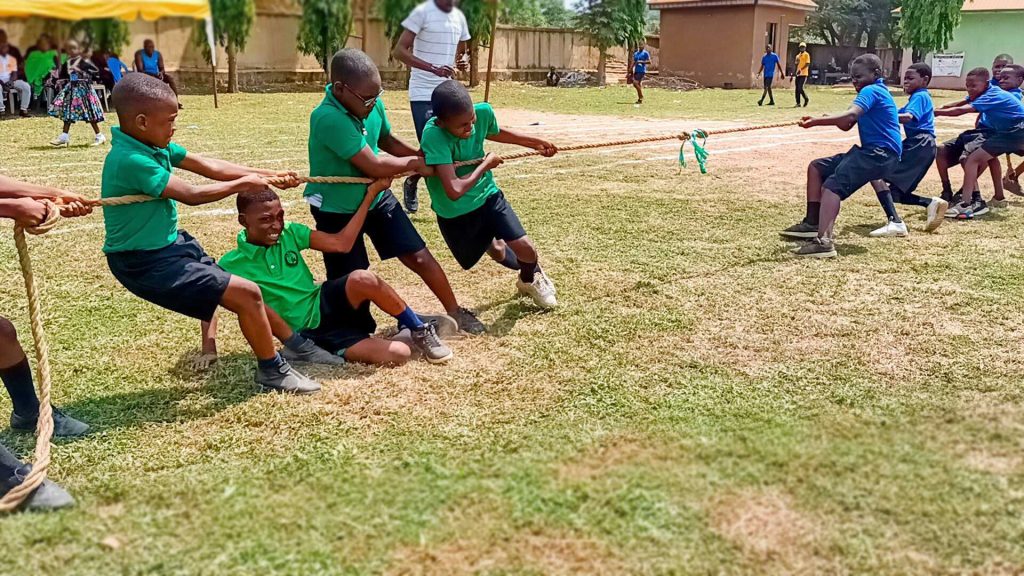
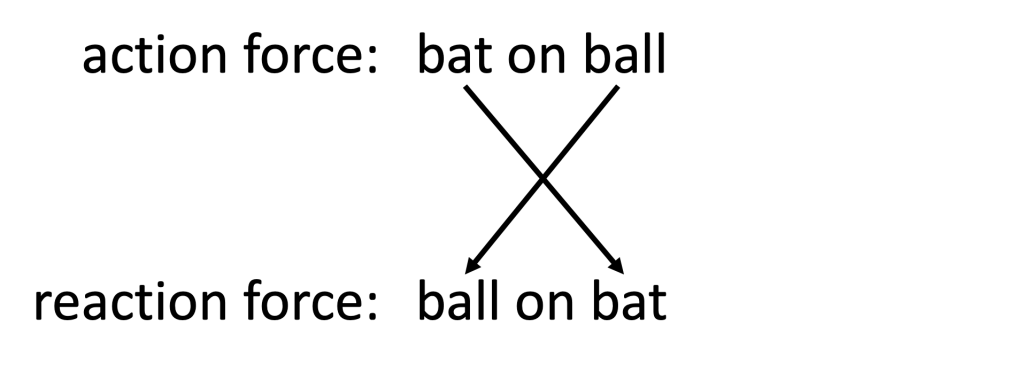
Finding action-reaction pairs

If you can identify an action force, you can determine the reaction force by switching the order of the nouns describing the force. For example: if the action force is that a baseball bat pushes against a ball, the reaction force is that the ball pushes against the baseball bat. Figure 5.3 demonstrates how to switch the order of each noun. The table below lists different action-reaction pair scenarios.

Gravity is a force where the Earth pulls you (and other objects) downward. What is the reaction force? Is the reaction force the support force between yourself and the floor? Consider the support force to be a push or a pull. The support force is the floor pushing up on you. These are NOT action-reaction pairs because the nouns are different. Furthermore: two forces that act on the same object cannot be action-reaction pairs.

What is the reaction force to gravity? The reaction force is that you are pulling up on the Earth. What is the reaction force to the support force? You are pushing down on the floor.

Newton’s third law can be considered to be the reason why things move. A rocket works by creating a chemical reaction that causes exhaust gases to be pushed out of the bottom of the engine. The reaction force is thrust provided by the gases acting on the rocket that causes the rocket to move upward. A jet engine also produces thrust by moving gases backward through a turbine engine.

Systems and external forces

A system is any collection of objects that we define. If there are two carts moving on a track, we can define a system as consisting of just one cart, or just the other cart, or both carts. In other words, a system can be defined however we choose. This concept is important in understanding how external forces can act on an object to change its motion. What do we consider to be an external force? While the concept of a system can be somewhat arbitrary, it can be useful when determining how to analyze the properties of an object or collection of objects.

Consider a horse pulling a cart along a road, as shown in Figure 5.4. If we consider the system to be the cart, then the horse is considered external to that system. From the perspective of the system, the horse exerts an external force on the cart which causes the cart to start moving.

What if we expand our view and define the system as consisting of both the cart and the horse? What is the external force that causes the system to move? In this case, we have to look outside of the horse-cart system for the answer. In this case, the force that causes the system to start moving forward is the reaction force that the Earth exerts on the horse’s hooves when the horse pushes backward on the ground.

But what if we continue to expand our view of the system to include everything: the cart, the horse, the Earth, everything? How can anything move if the definition of a system is arbitrary, and forces that may be external in one system are not external in another? How can things move if every action has an equal and opposite reaction force? Why don’t all forces just cancel out and cause everything to be in equilibrium all the time? Keep reading to find out!

Using Newton’s second and third laws

If every force causes an equal and opposite counter-force, why isn’t everything in equilibrium? The reason is that while all forces have equal and opposite reaction forces, the effect of those forces depends on the object they act on. We can use Newton’s second and third laws together to get an idea of why this is.

As you walk, run, or roll around, you are able to change your motion. It is possible to change your motion by pushing off the floor. The reaction force is that the floor pushes back on you. It is this reaction force that causes us to move. (This is true both for feet and wheels.)

Why is it that we move when we walk, run, or roll, but the floor does not move? Think about the floor: it is attached to a building that’s probably extremely massive and hard to move. It has a lot of inertia. Compared to the building, we are relatively small and don’t have much mass. While we experience equal forces, we do not experience equal accelerations, or changes in our motion, as a result of that force.

Consider a hypothetical example where you accidentally drop your smartphone on the ground. The approximate mass of a smartphone is 0.16 kg (160 g). The Earth’s gravitational field causes the smartphone to have an acceleration of 9.8 m/s² (pointing downward). Using Newton’s second law to calculate the net force on the smartphone, we find that

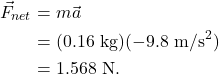
The Earth pulls down on the smartphone with a net force of 1.568 N.

The reaction force is that the smartphone pulls up on the Earth with a force of 1.568 N: equal and opposite. Why can’t we see the effect of this reaction force? The reason is that the Earth is extremely massive and its inertia makes it exceptionally difficult to move. Using Newton’s second law to calculate the acceleration of the Earth due to the smartphone, we find that

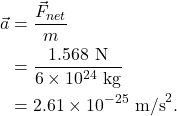
This calculation concludes that the acceleration of the Earth is , which is immeasurably small, so it is essentially zero.

Even if you drop something with a mass of thousands of kilograms, or a million kilograms, or a billion kilograms, the acceleration of the Earth would still be essentially zero. The Earth is extremely massive; it’s massive on literally a planetary scale. So it would take an object of comparable mass and size to make any noticeable effect on the Earth’s motion.

Every object that the Earth pulls down, pulls the Earth up with equal magnitude. You are pulling up on the Earth yourself, and do so all the time! Just because there are equal and opposite forces does not mean there is equal and opposite motion. The Earth can cause us to accelerate very readily, whereas we do not make even a tiny budge to the Earth’s motion.

Practice questions

Conceptual comprehension

1. List as many action-reaction pairs as you can for forces acting on yourself or objects that you can see right now.
2. An unfortunate mosquito flies into the windshield of a sports car driving 100 KPH down the highway. Which object (the squashed mosquito or the sports car), if any, experiences a greater force in this impact? How do you know?

Numerical analysis

1. A person (with a mass of 80 kg) standing on a frictionless surface kicks a 5 kg rock with a force of 10 N. Calculate the…
   1. …magnitude of the force that the rock exerts on the person during the kick.
   2. …acceleration of the person.
   3. …acceleration of the rock.
2. The Saturn V rocket had a mass of 3,000,000 kg and generated 350,000 N of thrust. As the engine pushes against the Earth (which has a mass of approximately 6 x 10²⁴ kg), calculate the…
   1. …magnitude of the force the Earth exerted on the rocket.
   2. …acceleration of the rocket.
   3. …acceleration of the Earth.

Hands-on experiments

1. If you have a balloon, string, and straw, build a balloon rocket. Consider the action and reaction forces that contribute to the motion of the balloon.