15. Temperature and heat
Summary
Temperature
Temperature quantitatively describes the average translational kinetic energy of the atoms and molecules in a substance. It quantifies the “hotness” or “coldness” of something. The symbol for temperature is the uppercase letter 
.
Kinetic energy describes the energy of motion. Therefore, it would be reasonable to expect that a substance at a higher temperature will have more motion than a substance at a lower temperature.
In the video below, there are two beakers filled with water. The beaker on the left is filled with cold water, and the beaker on the right is filled with hot water. (The beaker on the left appears translucent due to the fact that water vapor from the air has condensed on it.)
A drop of blue food dye is dropped into each beaker. After watching for several moments, you can see the food dye swirl around and distribute itself much more rapidly in the beaker of hot water, demonstrating that its motion is much greater than that of the cold water. A photograph of each beaker 30 seconds after the introduction of the food dye is shown in Figure 15.1. The dye in the cold beaker (left) has not distributed nearly as much as the dye in the hot beaker (right).
From a human perspective, temperature is extremely important in helping us determine what to wear when we go outside, and in deciding on what types of indoor and outdoor activities we want to do. Having an objective temperature scale is important in that it cuts out the subjective interpretation of each person’s idea of what may be “hot” or “cold.” From a physics perspective, an objective temperature scale enables scientists to perform experiments on thermodynamics, climate change, and other important phenomena.
Empirical temperature scales
Now that we understand what temperature is, we need a way to measure it. There are two types of temperature scales that can be used: empirical scales and absolute scales.
An empirical scale means that experiments were performed to derive the upper and lower limits of the scale. The Fahrenheit scale was proposed in the 1700s. The limit for the cold end of the temperature scale was a frozen salt water solution. That temperature was denoted as zero. The limit for the hot end of the temperature scale was the temperature of a human body. This temperature was denoted at 96. (This value was chosen because it is easily divisible by many numbers; it has 12 divisors.) The total number of degrees on this scale was therefore 96, creating the original Fahrenheit temperature scale. This rudimentary scale is shown in Figure 15.2.
The basis of the Fahrenheit scale isn’t terribly scientific because it’s not repeatable. Depending on how much salt is placed in the freezing salt water solution, and whether or not the person whose body temperature is measured is sick with a fever, there will be different definitions of 0 and 96 Fahrenheit. Even if we standardize how much salt to place in the water, we are still limited by the variations in human body temperature.
Since the development of the Fahrenheit scale, it has been standardized such that temperature measurements using this scale are now repeatable and scientific. This allows meteorologists (and others) in the United States (one of the only countries in the world that continues to use this scale) to record temperatures in degrees Fahrenheit that are comparable from day to day and over time. While the Fahrenheit scale is admittedly useful as a temperature scale, as we tend to experience the full range of temperatures from zero to one hundred (particularly in varied climates), it was not created with a scientifically sound basis.
The Celsius scale was also developed in the 1700s. The cold end of the temperature scale is established by the freezing point of water at 1 atm of pressure, and is called zero Celsius. (A photograph of a Celsius thermometer reading zero degrees in a bath of ice water is shown in Figure 15.3.) The hot end of the temperature scale is established by the boiling point of water at 1 atm of pressure, and is called one hundred Celsius. This means that there are 100 degrees between the cold and hot ends of the Celsius scale. (Note that the original Celsius scale was actually inverted such that 0 degrees indicated the boiling point of water, and 100 degrees indicated the freezing point of water.)
The selection of the cold and hot ends of the thermometer establishes the temperature scale and allows us to measure temperatures in between those two extremes. (We can also extrapolate to measure temperatures that are hotter or colder.) This is shown in Figure 15.4.
Celsius is a scientific scale because it’s repeatable. As long as two (or more) scientists use pure water, and freeze and melt that water at one atmosphere of pressure, they will develop identical temperature scales. Because of this, Celsius is the scale that we will use, almost exclusively, to discuss temperature in this textbook.
Although we will not be using the Fahrenheit scale in this textbook, it is still useful to understand how to convert between the Fahrenheit and Celsius scales. To convert between scales, we need to know where the two scales overlap with each other, and how much of a change in one scale relates to a change in the other scale. On the first point: 0 oC is equal to 32 oF. On the second point: a change in 1 Co is equal to a change in 1.8 Fo. (Note the use of the symbol Co to denote a Celsius degree, which is used to distinguish a change in temperature from a temperature value.) Therefore, to convert from degrees Celsius to degrees Fahrenheit, take the temperature in Celsius, multiply by 1.8, and add 32:
To convert from degrees Fahrenheit to degrees Celsius, take the temperature in Fahrenheit and subtract 32 from it. Multiply the result of that subtraction by five-ninths. The result is the temperature in degrees Celsius:
Absolute temperature scales
The other type of temperature scale that can be used is called an absolute scale. Absolute scales are designed by establishing the lower limit based on a physical limitation. As we will discuss later in this textbook, there is a lowest possible temperature that can be achieved. That limit is known as absolute zero. As far as we know, nothing can be colder than absolute zero. This establishes the lower limit of our absolute scale.
The absolute scale that’s used in physics is known as the Kelvin scale. The zero end of the Kelvin scale is absolute zero. Because there’s no upper limit to the temperature of an object, there is no upper limit to the scale. (In fact, the upper limit is bounded by the total amount of energy that exists in the universe.) How do we establish the gradations of each unit of kelvin? The Kelvin scale was developed so that a change in one kelvin is equal to a change in one Celsius degree.
Absolute zero is equal to -273 oC. Therefore, to convert from degrees Celsius to kelvin, simply add 273:
To convert from kelvin to degrees Celsius, subtract 273:
Just a note to check your work: there is no such thing as a negative temperature in the Kelvin scale, so if you get a negative answer when converting to kelvin, check your math!
Thermometers
To measure temperature, a thermometer is used. How do thermometers work, and how are they designed?
In general, a thermometer exploits a thermometric property of a substance. A thermometric property is simply a property of the substance that varies with temperature. To achieve the best sensitivity for a thermometer, you want to choose a property that has a very large variation for small changes in temperature. Most analog thermometers (see, for example, Figure 15.5) contain a substance that will remain a liquid at all temperatures that the thermometer can reasonably be expected to experience. For example, in geographic regions with hot summers and cold winters, a thermometer would need to remain liquid between temperatures of roughly -20 oC and +40 oC. Modern thermometers are generally filled with dyed ethyl alcohol, which remains liquid between temperatures of -114 oC and +78 oC. (Previously, thermometers were filled with mercury, which remains liquid to much higher temperatures, but which is a hazardous toxic element.)
Materials such as liquids will generally expand as they heat and contract as they cool. That is, the thermometric property used is the volume of the substance. This means that as the thermometer is placed in cooler temperatures, the level of liquid will fall. As the thermometer is placed in hotter temperatures, the level of liquid will rise. To calibrate the thermometer, it can be placed in freezing water to establish the 0 oC point, placed in boiling water to determine the 100 oC point, and then 99 gradations placed in between. To determine the temperature at any given time, the level of liquid inside the thermometer can be read, as after a time it will have risen or fallen to the level corresponding to the current temperature.
A digital thermometer (shown in Figure 15.6, for example) has a device inside whose electrical properties are changed as a function of temperature. The thermometric property in this case of the resistivity of a semiconductor. The relationship between temperature and resistivity is well known. Therefore, by measuring the resistivity, the temperature can be determined. A microcontroller then converts that temperature into numbers and displays them on an LCD screen.
Heat
Heat is energy that is transferred from one object to another in response to a difference in temperature. The symbol for heat is the uppercase letter 
. Calories (cal) are the unit for heat. Because heat is a form of energy, joules is another unit that can be used to express heat.
Heat only spontaneously flows from hot to cold, and never spontaneously flows in the opposite direction. To relate this to something more familiar, consider it to be similar to gravity. If a ball is placed at the top of a ramp, gravity will pull the ball downward, causing it to roll down the ramp. Once the ball reaches the bottom of the ramp, gravity will not pull it back up to the top again. The only way for the ball to reach the top of the ramp is for a person, animal, or machine to expend energy in physically moving it back to the top again. Going against gravity requires work.
In much the same way, working against the established flow of heat takes work. Maybe you use a refrigerator or air conditioner. These seem to work against the flow of heat from hot to cold. And they do, but it requires energy to do this. If you’ve paid an electrical bill during a hot summer month when running the air conditioner, you know it’s not cheap to keep things cool. In other words, your refrigerator and air conditioner will not cool the regions you want unless you plug them in and turn them on!
Specific heat capacity
Specific heat capacity defines how difficult it is to change the temperature of a substance. (It can be thought of as “thermal inertia.”) The symbol for specific heat capacity is the lowercase letter 
. The unit is calories per gram degree Celsius (cal/(goC)). Specific heat capacity describes how many calories of heat are required to increase (or decrease) the temperature of a certain mass of material by a certain amount.
The equation that relates heat, specific heat capacity, mass, and change in temperature is
where is the heat (measured in calories), 
is the mass (measured in grams), is the specific heat capacity, and 
is the temperature change (measured in degrees Celsius).
It is important to note that this equation only works when the temperature of a substance changes, and cannot be used when an item changes phase, for example to calculate the heat required to boil water.
The specific heat capacity of water is 1 cal/(gCo). This means that 1 calorie of heat is required to raise the temperature of a single gram of water by one Celsius degree. (The calorie unit was actually defined on this basis; one calorie was equal to the amount of heat required to increase the temperature of one gram of water by one Celsius degree.) This may not seem like a lot, but water actually has one of the highest specific heat capacities of common substances. It makes water a very good candidate for use in cooling systems, because it can absorb a lot of heat without changing its temperature very much.
Large calories and small calories
The unit of calorie may be familiar if you have looked at the nutrition label for food (such as the one shown in Figure 15.7). The unit of calorie used in food products does relate to the amount of heat required to raise the temperature of water by one Celsius degree, however, in this case, the amount of water is one kilogram, not one gram! These calories are known as “large calories,” “food calories,” or “kilogram calories” and are sometimes specifically spelled out as Calories with a capital C to distinguish them from the so-called small calorie described above.
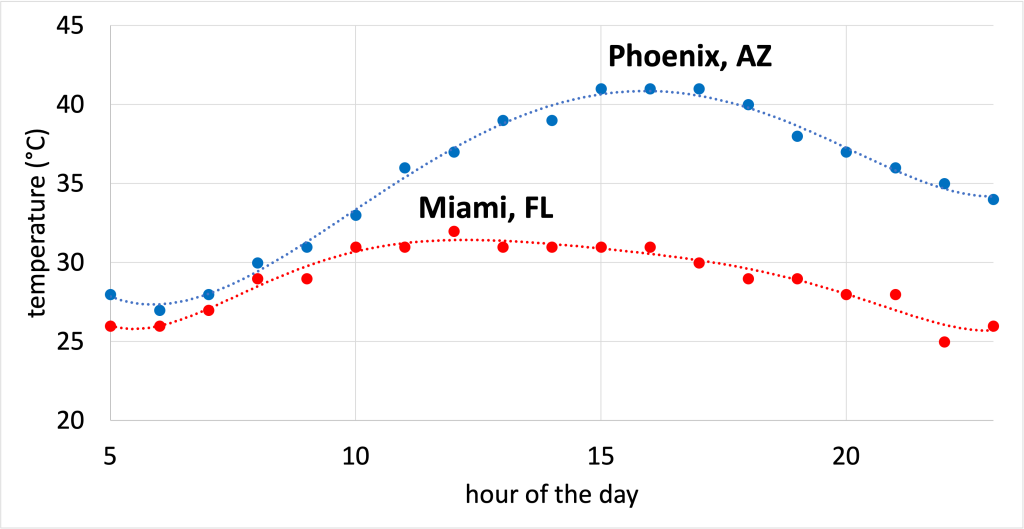
This fact also explains why the climate tends to be milder if you live near a large body of water. This could be an ocean, or even a large lake such as Lake Michigan. Because the water in an ocean or lake doesn’t change its temperature easily, it means that the water will act as a moderating influence as the seasons change. This also explains why daily temperature fluctuations are much larger in the desert than they are in wetter climates. Humidity in the air acts as a moderating influence to keep temperatures from swinging to extremes between night and day. For example, Figure 15.8 shows the hourly temperature in Phoenix, AZ and Miami, FL on September 14, 2021. (Download this data [XLSX, 9 kB]) In Phoenix, a desert, the temperature demonstrates a much greater variation than in Miami, a much wetter climate.
Temperature mixtures
When two substances at different initial temperatures are combined together, the hot substance will cool down and the cool substance will heat up until the two substances arrive at thermal equilibrium. At this point the temperature will remain constant. According to the law of conservation of energy, the energy that is lost by the hot substance will be completely transferred to the cool substance. (This assumes that no heat is lost to the surroundings.) In equation form,
Unless the two substances are composed of the same material with identical specific heat capacities and have the same mass, while both substances will experience a temperature change, the magnitude of change in temperature of each substance may not be the same. (For example, if the hot substance cools down by 10 Co, the cool object may not warm up by that same amount.) All other things being equal, a substance with a higher specific heat capacity will experience a smaller temperature change than a substance with a lower specific heat capacity.
To determine the final temperature of a mixture of two substances, the conservation of energy equation defined above can be substituted with 
to calculate 
. This equation is
The final temperature should be somewhere in between the two initial starting temperatures. (This is a good “smell test” to use to determine if your final temperature calculation makes sense.)
Thermal expansion
Substances tend to expand when they are heated. In fact, this property was utilized to create analog thermometers, as we saw earlier in this chapter! Because the molecules within the object have more motion as they heat up, it makes sense that most substances will expand when heated.
This is demonstrated in the video below. A metal ball and hoop start out at room temperature. The ball is easily able to pass through the hoop, demonstrating that the ball is smaller than the hoop’s opening. Dr. Pasquale heats up the ball with the blowtorch, which causes it to expand. It has expanded to such a degree that it is no longer able to fit through the hoop. Next, she heats up the hoop with the blowtorch. Because the hoop expands, now the ball is able to pass through again.
After the ball and hoop cool down again, they return to their original sizes.
Thermal expansion has some very important repercussions in our physical world. Notably, structural objects like bridges and buildings have to be engineered specifically to account for this expansion and contraction in hot and cold weather. Long bridges contain expansion joints (see Figure 15.9). This enables them to stretch out in the heat without buckling or breaking.
Power lines also experience thermal expansion, sometimes in devastating ways. In the summer, power lines expand due to the heat. Not only that, but the load on the electrical lines also increases on hot days due to people using their air conditioning units. The excess load causes even more heat in the power lines, causing them to expand even more. If the expansion causes the power line to come into contact with tree limbs or a bush, then a short circuit can occur. In extreme cases, this may cause the power grid to go offline. In fact, this was one of the contributing causes to the Northeast Blackout of 2003, which caused Dr. Pasquale’s family’s home to be out of power for a week!
You may notice that tree limbs are trimmed around power lines (see Figure 15.10). One reason for this is to prevent possible short circuits from occurring when the power lines sag.
It’s possible to engineer the thermal expansion of a material to be very similar to that of another substance. This is helpful for fillings we get in our teeth because of cavities. When we eat hot food, we want our teeth and the fillings inside of them to expand at the same rate. Composite fillings have been engineered to do just this.
What happens if two substances come together that have different rates of thermal expansion? The video below shows a bimetallic strip. That is, it’s made out of two different metals that are connected together. When Dr. Pasquale heats the bimetallic strip with a blowtorch, each metal expands at a different rate, causing it to curl up. The metal with the smaller thermal expansion expands less, which forces it to conform to the inner portion of the curve generated by the metal that expands more.
The bimetallic strip has found a practical application as an element in analog thermostats. A bimetal strip, when heated to a warm room temperature, will be coiled up. As the room cools down to a setpoint, the coil unfurls and eventually comes in contact with some type of sensor that sends a signal to the furnace to turn on and heat the room. Once the room heats up again, the strip coils up and deactivates the furnace. A thermostat using a bimetal strip is shown in Figure 15.11. A second bimetallic strip at the top of the device causes the pointer to indicate current room temperature. Similar bimetal coils are or have been used in refrigerators, computer cooling, and air conditioning systems.
Negative thermal expansion
While most substances expand when heated, not all of them do. A few substances will contract instead. This is known as negative thermal expansion. Most notably, water is densest at 4 oC. Below that temperature, water will expand. This is why ice cubes float on liquid water (see Figure 15.12). It’s also why aquatic life is able to exist on our planet. Because ice floats, as long as a body of water is deep enough, the water at the bottom will be four degrees Celsius at the coldest time of year, enabling aquatic life to remain alive instead of freezing every winter. The ice also acts as an insulating layer, protecting the water below from even colder air temperatures above the surface of the water.
Thermal stress
Whether objects expand or contract when heated, the molecules within the object need a sufficient amount of time to respond to these changes in size. Otherwise, it’s possible that the molecules inside an object will experience enough stress to cause them to break.
In the video below, Dr. Pasquale has a glass. There’s nothing wrong with it at the start, no scratches or defects at all. She heats the glass up with a blowtorch. Note that the glass stays intact, it just heats up. When Dr. Pasquale plunges the glass into a container filled with ice-cold water, the glass breaks. This is because the expansion and contraction isn’t given enough time to occur without causing huge amounts of stress in the glass.
Thermal stress means that we have to be careful with the types of materials we use in and on our stoves and ovens. Specially tempered glass like PyrexTM is used when wide swings of temperature are expected. (Note that PyrexTM cannot necessarily be placed in an oven at any temperature!)
Further reading
- SI Units – Temperature – This website from NIST explains the Kelvin and Celsius temperature scales and provides a reference to Fahrenheit as well.
Practice questions
Numerical analysis
- If the temperature is 20 oC, calculate the temperature in…
- …Fahrenheit.
- …kelvin.
- If the temperature is 75 oF, calculate the temperature in…
- …Celsius.
- …kelvin.
- If the temperature is 318 K, calculate the temperature in…
- …Celsius.
- …Fahrenheit.
- Calculate the amount of heat required to change the temperature of 500 g of water from 25 oC to 45 oC.
- Calculate the amount of heat required to change the temperature of 250 g of aluminum from 20 oC to 80 oC. The specific heat capacity of aluminum is 0.215 cal/goC.
- Calculate the amount of heat required to change the temperature of 2 kg of lead from 100 oC to 200 oC. The specific heat capacity of lead is 0.031 cal/goC.
- Calculate the amount of heat required to change the temperature of 800 g of water inside a 500 g copper kettle from 20 oC to 100 oC. (No phase change occurs in this process.) The specific heat capacity of copper is 0.092 cal/goC.
- Calculate the final temperature of a mixture of equal amounts of water at 20 oC and water at 80 oC.
- Calculate the final temperature of a mixture of 10 g of water at 30 oC and 40 g of water at 90 oC.
- If 200 grams of water at 20 oC are mixed with 300 grams of ethanol at 30 oC, calculate the final temperature of the mixture. The specific heat capacity of ethanol is 0.584 cal/goC.
- You mix 400 g of iron at 80 oC with 600 g of water at 25 oC. Calculate the final temperature of the mixture. The specific heat capacity of iron is 0.11 cal/goC.
Temperature defines the average kinetic energy of an object. It quantifies the “hotness” or “coldness” of something. (symbol: T, unit: °C or K)
Kinetic energy is the energy that an object has due to its motion. (symbol: KE, unit: J)
Energy is defined as the capability of an object (or collection of objects) to do useful work. (symbol: E, unit: J)
An object is translucent if it allows light to pass through, but scatters that light in the process.
Physics is a branch of science that focuses on the fundamentals of the workings of our universe.
Thermodynamics is the study of heat flow and its relationship to temperature, work, energy, and entropy.
Freezing is the phase change from a liquid to a solid.
Pressure defines the amount of force applied over an area of a substance. (symbol: P, unit: Pa)
Absolute zero is the thermodynamic limit corresponding to the lowest possible temperature. Absolute zero is defined to be 0 K.
A liquid is a state of matter in which the constituent molecules will change their shape or arrangement but cannot be easily compressed to change their volume. Liquid is one of the four most common phases of matter.
An element is a substance that consists of atoms whose nuclei have the same atomic number. An element cannot be broken down further by chemical means.
Heat is energy that is transferred from one object to another in response to a difference in temperature. (symbol: Q, unit: cal)
Gravity is the attractive force experienced by objects of mass. It is one of the four fundamental forces.
Work is energy that is transferred to an object by exerting a force on that object over a distance. (symbol: W, unit: J)
Specific heat capacity defines how difficult it is to change the temperature of a substance. It describes the amount of heat required to change the temperature of a certain mass of a substance by a certain temperature. (symbol: c, unit: cal/(g°C))
Mass is a property of physical objects that relates to resistance to changes in motion: inertia. (symbol: m, unit: kg)
A short circuit is a circuit that contains a very low-resistance path along which electrons will travel. It can result in excess current, which may cause the circuit to overheat.
