14. Gases

The Earth’s atmosphere

The Earth’s atmosphere is a layer of gases that surrounds the planet. The atmosphere doesn’t just allow us to breathe, it also protects us from UV radiation, traps moisture and heat, and exerts a force on every surface it touches.

The composition of the Earth’s atmosphere is approximately 78% nitrogen, 21% oxygen, and 1% argon. There are also trace amounts of some other gases in our atmosphere: carbon dioxide, water vapor, and others.

Because gas molecules are not in contact with each other (except during very brief collisions), gases can be compressed. The atmosphere will be denser at sea level than at higher elevations and altitudes due to the weight of the molecules above pushing down on the molecules below. This is analogous to a human pyramid: in a human pyramid, the people at the bottom are compressed from the forces from all the people above (see Figure 14.1). In our atmosphere the molecules at the bottom are compressed from all the molecules above.

If we were to take a ride from sea level up and up and up, we would notice the density of the atmosphere decreasing with our altitude. At a certain point, we would require an oxygen tank to allow us to breathe. Though the composition of the atmosphere remains constant for about 100 kilometers, meaning that we still have 20% oxygen, the total number of molecules decreases when density decreases. This is why commercial airplanes have pressurized cabins as they fly through the stratosphere, and why many mountain climbers summiting Mount Everest will take oxygen with them.

The atmosphere of our planet has no real height to it. There is no point in our journey up and up to higher altitudes where the atmosphere stops. Instead, it is more of a gradient. There are a lot of atmospheric molecules close to the surface of the Earth, and fewer and fewer as altitude increases. Most of the mass of the Earth’s atmosphere exists below 100 kilometers, known as the Kármán line. This altitude is used as the designation of where “space” begins and the people who go beyond that altitude are considered to be astronauts. However, atmospheric phenomena such as auroras can still occur above this point.

Atmospheric pressure

At sea level, the pressure we experience due to the atmosphere is approximately 100,000 Pa. That means over a one square meter area, the force exerted by the atmosphere is equal to 100,000 newtons! This value of 100,000 Pa is also known as 1 atmosphere (atm) of pressure.

A device called a barometer is used to measure atmospheric pressure. Old barometers were made of tubes filled with mercury. As atmospheric pressure increased, more force was exerted on the mercury, which would rise up an evacuated tube and indicate higher pressure. A drawing of a mercury barometer is shown in Figure 14.2.If you’ve ever heard the units “millimeters of mercury” or “inches of mercury,” this is where those units of atmospheric pressure come from. Standard sea level pressure is 29.92 inches of mercury. (These units are really a misnomer. Millimeters and inches are units of height and not units of pressure. These units are a shorthand way of describing the pressure caused by a column of mercury that had the specified height.)

Aneroid barometers use compressible cells connected to a pointer to indicate pressure. As pressure increases, the cells are squished and the needle moves to higher values. As air pressure decreases, the cells expand and the needle indicates lower pressure values. An aneroid barometer is shown in Figure 14.3.

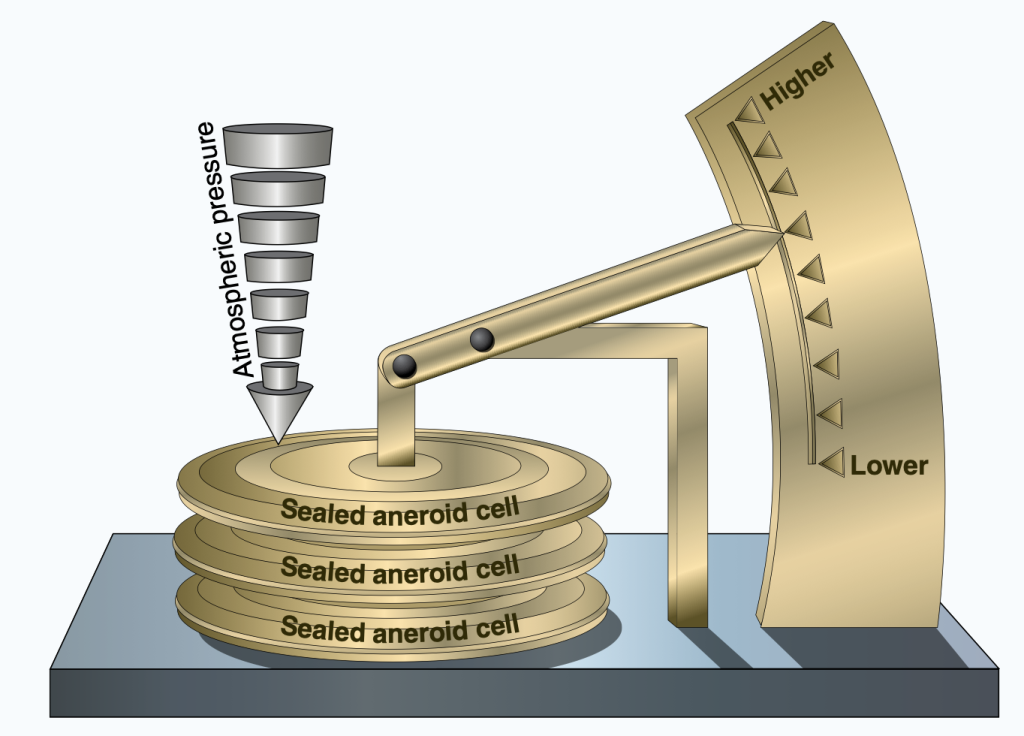
Today, many devices such as smartphones and watches use tiny barometers made of micrometer-sized electronics. Barometers are extremely useful devices in forecasting weather, and are an essential instrument in airplane control panels. An airplane instrument panel is shown in Figure 14.4. Three key instruments use atmospheric pressure to tell the pilot about the status of the airplane: the altimeter, the airspeed indicator, and the vertical speed indicator. While the instruments shown in Figure 14.4 are analog, even modern aircraft use digital displays of instruments that use the same physical concepts (essentially measuring air pressure).

Our atmosphere is capable of amazing things. Because we are constantly experiencing our atmosphere, we may not realize just how powerful atmospheric pressure is. Suction cups are capable of holding things up. Where does the counterforce to gravity come from? When air molecules are forced out from under the cup, there are many molecules pushing on the suction cup from the side, but very few molecules inside to push back. A really good suction cup can hold up quite a bit of weight. In Figure 14.5, a suction cup placed on a whiteboard holds up a 1 kg mass.

In the video below, Dr. Pasquale places larger and larger masses on the suction cup that’s placed on the whiteboard. At the conclusion of the video, she removes the suction cup from the board. When pulling directly outward on the suction cup, it’s nearly impossible to remove the suction cup, due to the large force created by air pressure pushing on the cup. In order to remove it, it is necessary to break the seal. Either pulling sideways on the suction cup, or pulling up on the edge, will cause air molecules to rush into the space between the suction cup and the whiteboard and break the seal.

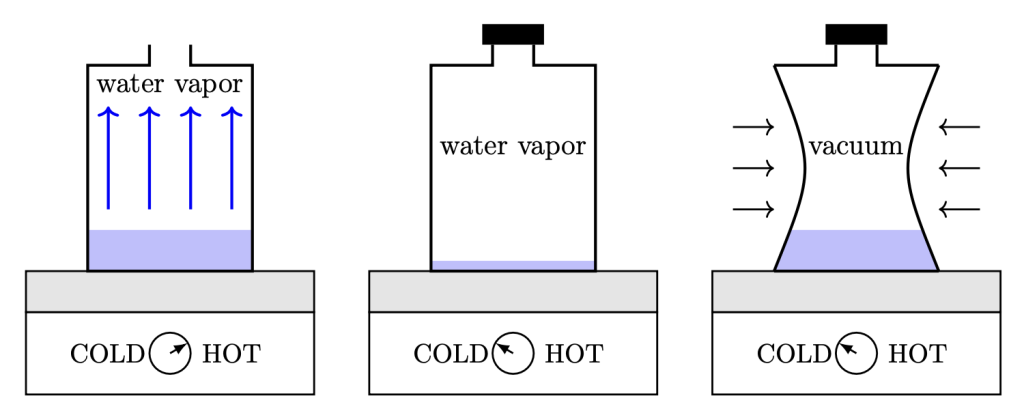
In the video below, Dr. Pasquale takes a metal can and removes the lid. She pours some water inside and places it onto a hot plate. The water heats up and begins to boil. Due to buoyancy, the hot water vapor rises and displaces the air, forcing most of the air molecules out of the can and into the surrounding room. At this point, Dr. Pasquale screws the cap back on tightly, and removes the can from the hot plate. Over time, the water vapor molecules inside the can cool down and convert back to their liquid form. When all of the water has condensed, there are very few molecules left inside the can, so very little pressure is being exerted outward on the can, but a lot of pressure is being exerted inward on the can. This causes it to collapse very dramatically!

The sequence of events that occurs in the can crush video is depicted in Figure 14.6.

Boyle’s law

Boyle’s law describes the relationship between pressure and volume of a fixed amount of gas when the temperature and number of molecules in a closed system are held constant. It states that the pressure times the volume is constant. In a closed system, if the volume decreases, it will cause the pressure to increase. If the volume increases, it will cause the pressure to decrease. We can state that in equation form as saying

where and are the pressure and volume at time one, and and are the pressure and volume at time two. In other words, the product of pressure and volume before the change is equal to the product of pressure and volume after the change as long as the temperature and amount of gas remain constant.

In the video below, Dr. Pasquale uses a cylinder and piston apparatus. The cylinder is closed, keeping the number of molecules of gas inside constant. A temperature gauge indicates a mostly constant temperature throughout the experiment. The volume of gas inside the cylinder is controlled by moving the piston up and down. A pressure gauge shows the pressure inside the cylinder, subtracting out the background atmospheric pressure. This is known as gauge pressure. Whereas absolute pressure is measured relative to vacuum, gauge pressure is measured relative to ambient atmospheric pressure. This can be related with the equation

As Dr. Pasquale decreases the volume of the cylinder, the pressure increases. It actually becomes hard to decrease the volume of the cylinder once it starts getting very small, due to the large amount of pressure that has built up in the cylinder.

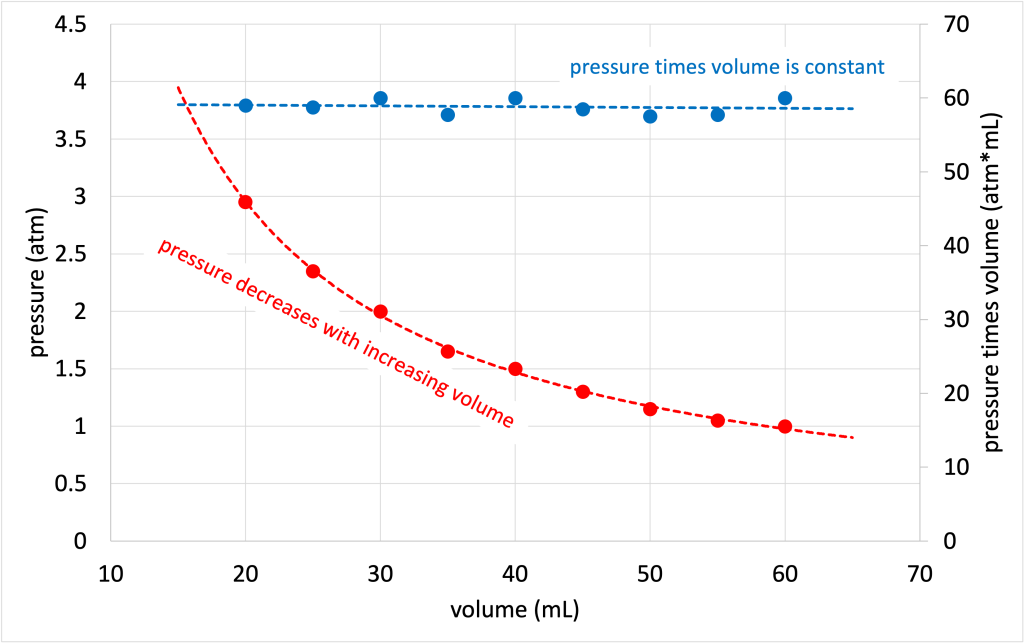
A graph of the pressure and volume relationship is shown in Figure 14.7. (Download this data [XLSX, 9 kB]) The pressure (converted to units of atm) decreases as the volume increases, showing a decreasing trend on the graph. The product of pressure and volume, however, remains constant with volume, as predicted by Boyle’s law.

In the video, once Dr. Pasquale compresses the cylinder all the way down, she releases the air. This causes the pressure gauge to indicate zero again. (The background atmospheric pressure has been subtracted out, as gauge pressure, not absolute pressure, is being measured. This is similar to a car tire pressure gauge: even if it indicates a pressure of zero for a flat tire, there is still one atmosphere of background atmospheric pressure inside the tire.) Now as she increases the volume of the cylinder, the pressure decreases, indicating negative on the pressure gauge. This relationship continues until she increases the volume back up to maximum again.

A more general version of Boyle’s law is the ideal gas law, which also considers temperature and the number of molecules involved. We will not go into details of this law other than to say that the ideal gas law tells us that the product of pressure times volume is proportional to temperature. In other words, as the temperature decreases, the product of pressure times volume decreases as well. If you have a car with an automatic tire pressure sensor, you may notice that it often triggers a low pressure alert in the winter due to the cold weather causing tire pressure to decrease.

Archimedes’ principle

As was discussed in the chapter on liquids, Archimedes’ principle discusses the buoyant force that exists when a fluid is displaced by another object. The buoyant force is equal to the weight of the displaced fluid. In liquids, this makes you feel lighter when you go swimming, for example. Both Archimedes’ principle and the principle of flotation exist in gases, too.

Any gas that is more dense than air will sink; any gas that is less dense than air will rise. Because the density of air decreases as the height above the surface of the Earth increases, any object that experiences a buoyant force will rise up until its density matches the surrounding density of the atmosphere.

In the video below, Dr. Pasquale has lit three candles in a large beaker. The beaker is initially just filled with air. She places a piece of solid carbon dioxide inside the beaker. The solid carbon dioxide sublimes, or turns directly into a gas (which is a process that will be discussed in chapter 17 of this textbook). The gaseous form of carbon dioxide is more dense than air. As the carbon dioxide builds up, it sinks and displaces the air in the beaker. Eventually the level of carbon dioxide rises up in the beaker and causes the candles to snuff out. Combustion requires oxygen to burn, and when the carbon dioxide displaces it, there is no more oxygen for the candles to remain lit.

Hot air balloons (shown in Figure 14.8) use buoyancy to fly. Hot air is less dense than cold air. Therefore, by heating up an envelope with hot air, we can achieve flight. Airships such as blimps achieve flight by using a gas that’s less dense than air, usually helium, inside their envelope. (Historically, a different gas that is less dense than air, hydrogen, was used in blimps. However, hydrogen is extremely flammable, and this led to the Hindenburg disaster. For this reason, hydrogen is no longer used as a buoyant gas in airships.)

If all it takes to rise up in our atmosphere is a less dense gas than air, why not use balloons to go to outer space? Consider a balloon filled up with helium gas. At sea level, helium is much less dense than the atmosphere. If you’ve ever let go of a helium-filled balloon, you’ve probably watched as it flew up into the sky. As the balloon rises, two things happen. The surrounding atmospheric pressure decreases with altitude. So the balloon will expand, and the difference in density between the balloon and its surroundings will decrease.

In the video below, Dr. Pasquale has a jar with an uninflated balloon. In the beginning, the surrounding pressure is relatively high and the volume of the balloon is low. It is safe to assume that the balloon is a closed system and that no molecules can either enter or exit through the balloon in any way. As Dr. Pasquale pumps air out of the jar, the volume of the balloon increases. The pressure in the balloon causes it to inflate because there are fewer molecules pushing in on it from outside.

If we picture this balloon on a journey upward through our atmosphere, one of two things will limit the balloon’s flight. Either the balloon will rise up to the point where its density is equal to that of the surrounding atmosphere. Or the balloon will expand to the point where the envelope of the balloon bursts. Balloons are certainly used for a lot of high-altitude research and weather measurements, but they are not a feasible method to achieve space flight. For that, we require rocketry.

Bernoulli’s principle

We just learned about two methods to fly around in our atmosphere: hot air balloons and blimps. What about airplanes and gliders? How do they work?

Bernoulli’s principle states that as the speed of a fluid increases, the pressure decreases. Another related principle is the Venturi effect, which states that as the area of fluid flow decreases, speed must increase. Both of these properties relate to airplane flight.

The venturi effect comes about due to conservation of mass. If there is a fluid flowing through some pipes, if a section of the pipe has a smaller cross-sectional area, then in order to get the same amount of mass flowing through, the fluid has to speed up in the smaller area. This is shown in an animation in the video below.

A carburetor (common in automobiles before fuel injection) uses the venturi effect to mix together gasoline and air to fuel a gas-powered internal combustion engine. While they are not common in automobiles anymore, they are still frequently encountered in the engines that power lawn mowers, chain saws, and small airplanes.

Bernoulli’s principle comes about due to conservation of energy. That fluid that speeds up now has more kinetic energy than the surrounding fluid. That additional energy has to come from somewhere since energy cannot be created or destroyed. As a result, the pressure of the fluid decreases in order to compensate. Whenever there is a difference in pressure on one side of an object compared to the other, there will be a net force.

In the video below, Dr. Fazzini demonstrates Bernoulli’s principle with two cans that are allowed to freely slide side-to-side by being placed on drinking straws. When he blows air in between the two cans, the increase in speed causes a decrease in pressure between the two cans, leading the two cans to bang into each other due to the greater pressure of the stagnant air on the outer sides of the two cans.

That video demonstrates a phenomenon you may have noticed if passing a large truck at high speed on the highway. As the airflow between two vehicles (particularly a large one such as a truck) becomes faster than the surrounding airflow, Bernoulli’s principle causes them to experience a force that tends to bring them together.

In this next demonstration of Bernoulli’s principle, Dr. Fazzini is able to deflect a candle flame (and blow the candle out) by deflecting airflow in different ways.

At first, Dr. Fazzini has a candle placed on the opposite side of a flat barrier from himself. When he blows air onto the barrier, it creates fast moving air that moves along the sides of the barrier, creating low pressure on the sides of the barrier. Air from immediately adjacent the opposite side of the barrier moves outward to fill into this low pressure area, and the result is that the candle flame deflects toward the barrier. This is depicted schematically in Figure 14.9.

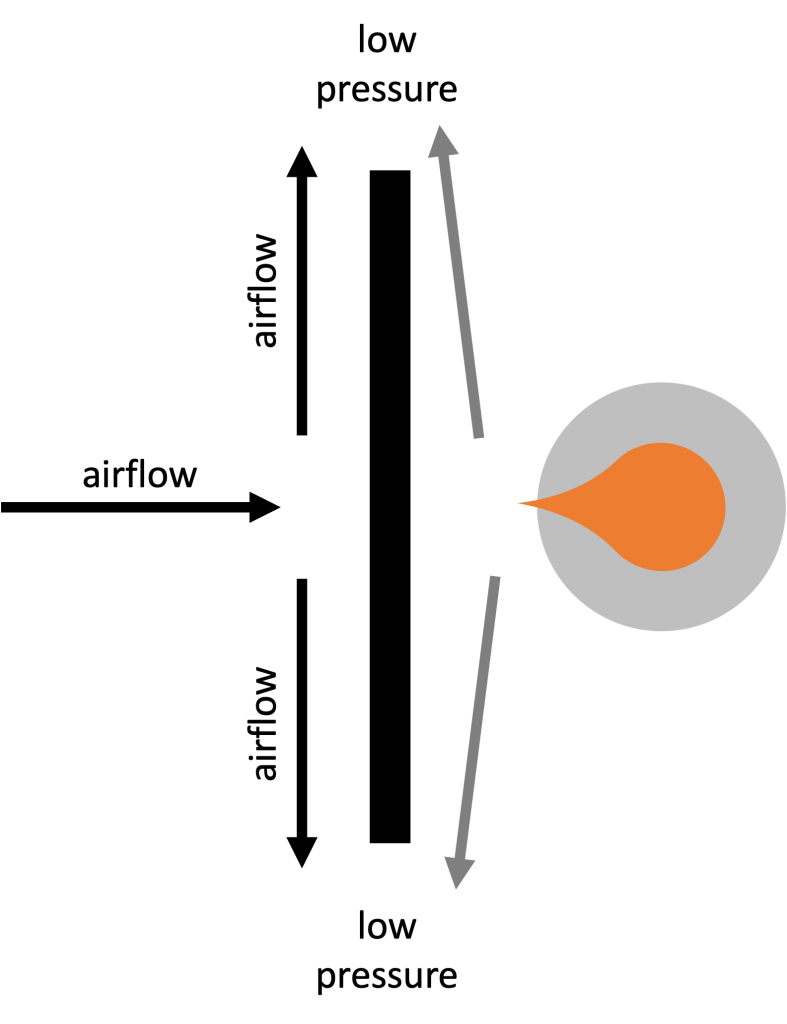
Next, Dr. Fazzini uses a circular barrier between himself and the candle. Now when he blows gently on the candle, the airflow streamlines along the circular barrier and causes the flame to deflect away from the barrier. When he blows hard enough, the candle is snuffed out.

As an additional demonstration of Bernoulli’s principle, in the video below, Dr. Fazzini attempts to fill two identical long plastic bags with air. Dr. Fazzini blows into the first bag five times. The volume of air is limited by his lung capacity. After five breaths, the air in the bag constitutes less than half of the bag’s total volume.

Next, Dr. Fazzini blows into the second bag. This time, he blows from a position slightly removed from the entrance to the bag. This causes an increase in airspeed, and a decrease in air pressure, causing air from around the room to fill in to that space and enter into the bag. In this case, much more of the bag is filled with air, even though only “one breath” was used to initiate this process.

In the video below, Dr. Fazzini again demonstrates Bernoulli’s principle with a ping-pong ball and a funnel. When he blows into the funnel, low pressure is created between the funnel and the ball, causing the ball to get “sucked in” to the funnel. He can hold the funnel upside down, and as long as he continues to blow into the funnel, the ping-pong ball will stay put in the funnel. However, as soon as he blows air above the ball, the ping-pong ball leaves the funnel. This is because the air blown above the ball causes low pressure above the ball and high pressure underneath. The net force is upward.

This next demonstration is similar to the ping-pong ball in the funnel demonstration, and gives further evidence to Bernoulli’s principle’s importance in flight. In the video below, Dr. Pasquale has a hair dryer and a foam ball. At first, she blows the air directly upward on the foam ball, pushing it up. As she tilts the hair dryer, she redirects the airflow, causing the air to flow faster above and slower below. Dr. Pasquale uses a string to show the airflow, which is moving very fast above the ball, and pretty much not at all below. This creates a pressure differential. The air pressure is lower on the top side of the ball, and higher on the bottom side of the ball. This causes a force of lift that counteracts gravity to keep the ball flying in the air. This is exactly the same physics that allows airplanes to fly!

In an airplane, the wings are angled so that the air moves faster over the top of the wing compared to the bottom of the wing. Bernoulli’s principle states that the fast air on the top of the wing has less pressure than the slow air on the bottom of the wing. This pressure difference leads to a force, which we call lift. As long as lift is initially greater than the weight of the airplane, the airplane will accelerate up into the air and fly! When the airplane is level in the air, the lift and weight vectors are equal and the airplane will maintain steady flight.

It should be pointed out that the physics that keeps airplanes in the air is more complicated than what is presented in this discussion. For example, aircraft can create lift while upside down. This is because other factors (not just the venturi and Bernoulli effects) are involved in the creation of lift. These factors include Newton’s third law, angle of attack (the angle that the chord of an airplane wing makes with respect to the relative wind), and camber (the shape of a wing). When the angle of attack is greater than zero (but less than a critical angle of attack at which point the airflow becomes detached from the wing), the airflow on the wing is deflected slightly downward. By Newton’s third law, the reaction force is that the wind pushes up on the wing. Both Bernoulli and Newton contribute to the overall explanation of how airplanes generate lift.

Plasma

The fourth of the four fundamental states of matter is plasma. Plasma is ionized gas. As previously discussed in this textbook, ions are atoms with an unequal number of protons and electrons. They contain a charge. A plasma is a gas where so much energy is present that electrons are removed from the atom. The resultant atoms of the plasma become positive ions floating in a sea of electrons. This separation of electric charge makes plasma capable of conducting electricity.

Plasma is the most abundant state of matter in the universe, as stars are made of plasma. Lightning, gas discharge lamps (such as neon lights), and the aurora lights are all examples of plasma that we may experience here on Earth.

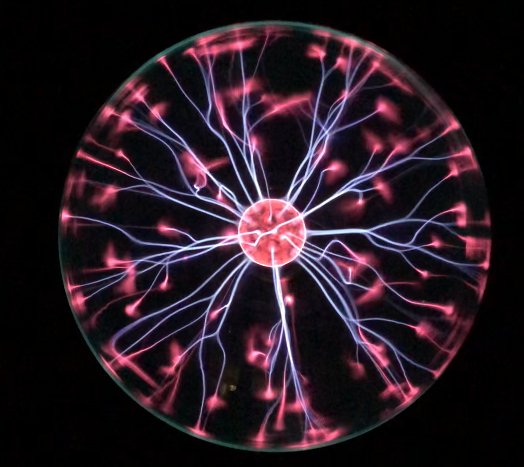
Plasma is particularly valuable as a method of creating light (which will be discussed in much greater detail later in this textbook). For now, it’s enough to know that plasma is how many different types of lighting work: fluorescent light, neon light, and sodium street lights. A plasma lamp, as shown in Figure 14.10, generates very colorful plasma emissions as a result of electric discharge.

Further reading

• Why don’t I feel the miles of air above me that are crushing me down? – This article explains why the force of atmospheric pressure (100,000 N per square meter!) doesn’t crush us.

Practice questions

Numerical analysis

1. A gas in a closed container has an initial volume of 4 L and a pressure of 3 atm. If the pressure is reduced to 1.5 atm while keeping the temperature constant, calculate the new volume of the gas.
2. A sample of gas occupies a volume of 10 L at a pressure of 200 kPa. If the pressure is increased to 400 kPa while keeping the number of gas molecules (and temperature) constant, calculate the new volume of the gas.
3. If a gas occupies a volume of 8 L at a pressure of 4 atm, calculate the pressure of the gas if the volume is reduced to 2 L while keeping the temperature and number of molecules constant.
4. A weather balloon is released into the atmosphere with a volume of 10 m³ at a pressure of 100 kPa. As the balloon ascends, the pressure decreases to 30 kPa. Calculate the final volume of the balloon when it reaches this lower pressure region (you can assume the temperature remains constant, as does the number of gas molecules inside the balloon).
5. A helium-filled balloon has a volume of 5 m³. If the density of helium is 0.18 kg/m³ and the density of air is approximately 1.2 kg/m³, calculate the buoyant force on the balloon when released into the atmosphere.

Hands-on experiments

1. If you have a drinking straw, place it into a cup or glass that’s filled with water. Cover the top of the straw with your finger, then lift it out of the glass of water. What happens to the water that’s in the straw? How does this relate to the topics discussed in this chapter?