34. Fission and fusion

Summary

This chapter will discuss the energy that can be harnessed by the atomic nucleus in the processes of nuclear fission (the splitting of heavy atomic nuclei into lighter pieces) and fusion (the combining of light atomic nuclei into a heavier piece).

Fission

As previously discussed, radioactive decay occurs when an atomic nucleus is unstable. This can happen due to the presence of so many protons that electromagnetic repulsion becomes stronger than the strong nuclear force that otherwise keeps the nucleus of an atom glued together, or when there are too many neutrons for the strong nuclear force to keep the unstable neutrons from decaying. The discussion that follows focuses on the former.

An atomic nucleus is not a static object. The nucleons (protons and neutrons) in the nucleus vibrate and jiggle around like a liquid drop. This internal motion can cause the nucleus to occasionally stretch into an elongated shape. If this elongation exceeds a critical amount, the electrical repulsion can overcome the strong nuclear force, causing the nucleus to pinch in the middle and then split apart. This is depicted in Figure 34.1. While rare, this does happen naturally, particularly in uranium and elements of greater atomic number. (Elements with atomic number greater than 92 are called transuranic.) This naturally occurring splitting is called spontaneous nuclear fission.

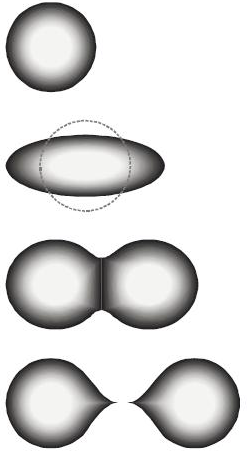
A depiction of the elongation and fission of a nucleus. At the top is a single nucleus, depicted as a sphere. The next image is an elongated nucleus, depicted as an oval shape. The next image shows the nucleus splitting apart into two spheres.
Figure 34.1 – A circular atomic nucleus may become elongated. At this point, the force of electrostatic repulsion becomes stronger than the strong nuclear force and the nucleus will pinch in the middle and split apart. Stages of nuclear fission (liquid drop model), by Hullernuc, is licensed under CC BY-SA 3.0.

If instead we artificially elongate a heavy nucleus, say by bombarding it with a neutron, the nucleus can be induced to elongate beyond the critical point so that electromagnetic repulsion will cause the atom to split in two roughly equal pieces. This process is known as induced nuclear fission.

Nuclear fission was discovered in 1938 by scientists Otto Hahn, Fritz Strassmann, and Lise Meitner when they found that barium isotopes were being produced after bombarding uranium-238 nuclei with neutrons. Lise Meitner and her nephew Otto Frisch came up with the theoretical explanation of what was occurring in these observations.

The process of nuclear fission not only causes the generation of two different nuclei from one original nucleus, it also releases a lot of energy in the process. Where does this energy come from? Consider a nucleus that will undergo fission. We carefully measure its mass before the fission process occurs. After bombarding the nucleus with a neutron, the nucleus fragments into two new nuclei (and some stray neutrons). If we carefully measure the mass of all of the byproducts of the fission process, that mass will actually be smaller than the original mass…by a very small amount.

We’ve talked about conservation of energy. Interestingly, in addition to other possible forms of energy, matter has energy due to its mass. This mass-energy must be taken into account when considering energy conservation, particularly in nuclear interactions. Mass and energy are related by Albert Einstein’s famous equation

    $$E = mc^2,$$

where E is the energy that something has by virtue of its mass m, and c is the speed of light. Note that this formula indicates that a tiny amount of mass contains a very large amount of energy (since the speed of light squared is a huge quantity).

The energy liberated in the fission process comes from the mass that is lost during the fission process. This equation basically identifies mass as another form of stored energy. Because the speed of light is such a large number, even a small amount of mass has the potential to release an enormous amount of energy. When Meitner calculated the mass of all the constituents before and after the reaction, it was found that the energy released in the reaction was equal to the energy calculated from the mass difference before and after the reactions. That is,

    $$E_{released} = \Delta mc^2.$$

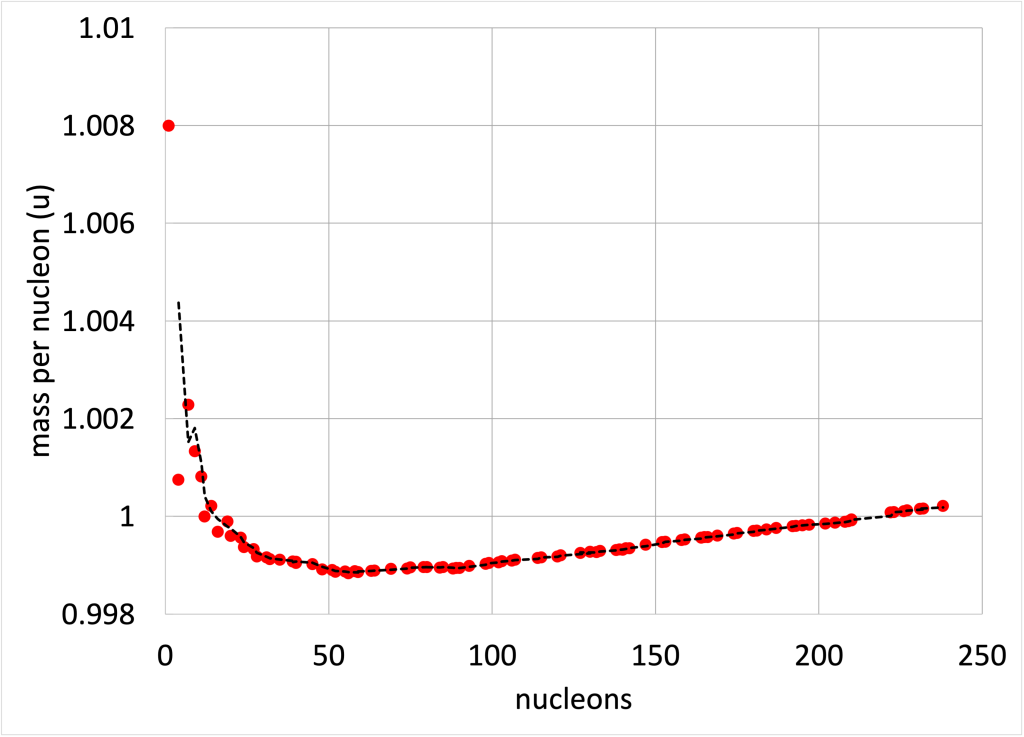
Can all atoms be used to generate energy by way of fission? The short answer is no. Very heavy atoms are capable of releasing energy from fission. Very small atoms are enormously hard to split apart due to their small size and the power of the strong force. If we look at a graph of mass per nucleon in an atom (shown in Figure 34.2), a hydrogen atom has a lot of mass in its one nucleon. On the other end of the spectrum is uranium. In between, with the least mass per nucleon, is iron. Atoms heavier than iron can release energy when they undergo nuclear fission. But the most energy will be generated with the heaviest atoms, and uranium-235 is the source of most nuclear power generated in the United States. (Note that u, the unit used on the y-axis of Figure 34.2, describes mass, and will be defined at the end of this chapter.)

A graphic depicting the mass per nucleon on the y-axis and number of nucleons on the x-axis. For the most part, the mass per nucleon starts large with hydrogen and decreases until iron, then increases slightly again through to uranium.
Figure 34.2 – A graph depicting the mass per nucleon of elements between hydrogen and uranium. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Uranium-235 is a fissile isotope of uranium. When a neutron is shot at uranium-235, the uranium-235 can capture the neutron to become uranium-236. The uranium-236 then fissions with one possible set of byproducts being krypton-92, barium-141, and three neutrons:

    $$^{235}_{92}\textrm{U} + ^{1}_{0}\textrm{n} \rightarrow ^{236}_{92}\textrm{U} \rightarrow ^{89}_{36}\textrm{Kr} + ^{144}_{56}\textrm{Ba} + ^{3}_{0}\textrm{n}.$$

This process is depicted in Figure 34.3.

A graphic showing a neutron hitting uranium-235, which briefly becomes uranium-236 before splitting into barium-144, krypton-89, and three new neutrons.
Figure 34.3 – The fission of uranium-235 leads to the generation of an isotope of krypton, barium, and three neutrons. Nuclear fission reaction, by MikeRun, is licensed under CC BY-SA 4.0.

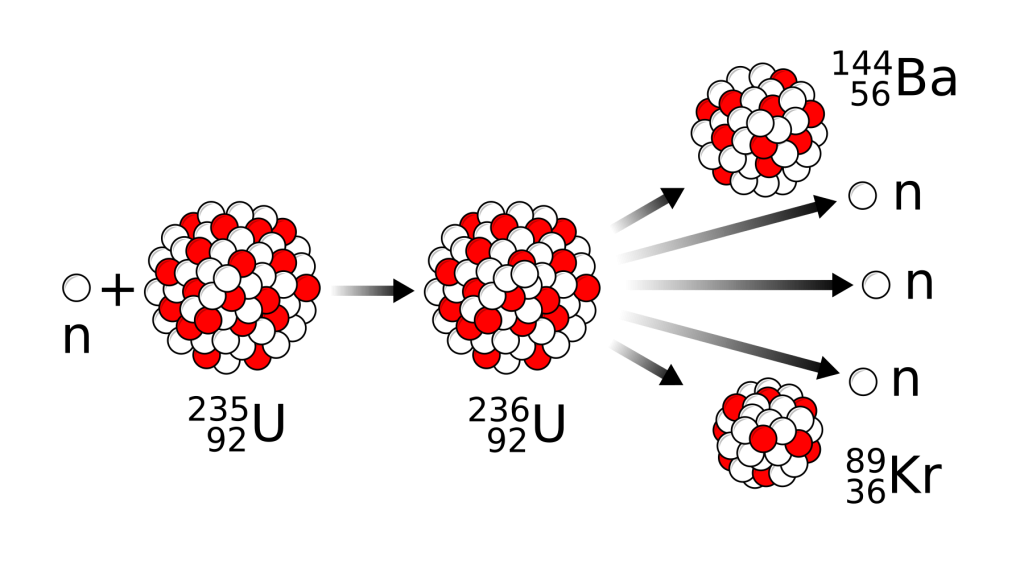
The total number of nucleons is conserved in this process, as is the charge and total energy. As mentioned, while mass is not conserved, mass-energy is.

Usually, the fission process is started by shooting a neutron at an atom to cause the elongation. Why is a neutron used instead of a proton? The neutron, being neutral, will not undergo any electromagnetic repulsion forces that would cause it to deflect away from an atomic nucleus. This is why neutron bombardment is a good method to explore atomic structure.

Some fission reactions liberate even more neutrons. If enough fissionable material is present, the liberation of new neutrons after each fission event can start what is known as a chain reaction: a self-sustaining reaction that doesn’t require any intervention to keep it going.

When a large enough quantity, known as a critical mass, of fissionable material is present, the energy is released so quickly that an explosion can result, releasing a massive amount of energy in a very short time. This is the principle behind nuclear weapons.

Fissionable vs. fissile nuclei

All unstable nuclei that will undergo fission after being bombarded with a suitable neutron are known as fissionable. However, it’s possible that some nuclei require neutrons with a very large amount of energy before they will undergo fission. Neutrons with a lot of energy travel very fast, and their de Broglie wavelength is therefore quite small. The de Broglie wavelength is qualitatively related to the likelihood of the neutron being captured by a nucleus. The smaller the wavelength, the lower the odds of being captured by a nucleus. This means that fissionable nuclei that require high-energy neutrons do not necessarily undergo the fission process in an efficient manner.

A fissile nucleus is an isotope that can undergo fission after being bombarded with slow neutrons (known as “thermal” neutrons). These neutrons, because they move slowly, have a larger de Broglie wavelength and therefore have a higher chance of interacting with fissile nuclei. A fissile isotope does not require as much material to be present to sustain a nuclear chain reaction. (Fissile isotopes are a subset of fissionable isotopes. All fissile nuclei are fissionable, but not all fissionable nuclei are fissile. For example both uranium-235 and uranium-238 are fissionable. However, while uranium-235 is fissile, uranium-238 is not.)

Chain reactions

A chain reaction is a self-sustaining fission process. For instance, after the fission process, a uranium-235 nucleus can liberate two or three new neutrons depending on the daughter nuclei. If a sufficient amount of uranium-235 is present, the liberated new neutrons will cause more of the atoms to undergo fission, which will release more neutrons, create more fission, and so on. This is shown in Figure 34.4.

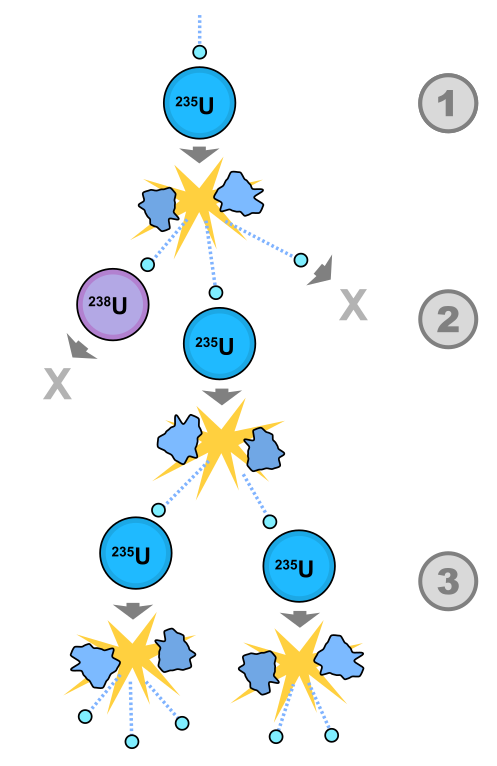
A schematic depcting a nuclear fission chain reaction. 1. A uranium-235 atom absorbs a neutron and fissions into two new atoms (fission fragments), releasing three new neutrons and some binding energy. 2. One of those neutrons is absorbed by an atom of uranium-238 and does not continue the reaction. Another neutron is simply lost and does not collide with anything, also not continuing the reaction. However, the one neutron does collide with an atom of uranium-235, which then fissions and releases two neutrons and some binding energy. 3. Both of those neutrons collide with uranium-235 atoms, each of which fissions and releases between one and three neutrons, which can then continue the reaction.
Figure 34.4 – In a chain reaction, enough neutrons are generated from each fission process to create a self-sustatining fission reaction. Fission chain reaction, by Fastfission, is licensed under Public Domain.

Although two or three neutrons are liberated in each fission, it is not necessarily true that each single fission process will produce two or three more. It’s possible some of the excess neutrons may escape the material, or be absorbed by a different nucleus, such as those in a control rod, to keep a nuclear reaction from generating too much energy.

The number of reactions that are provoked by a single fission event relates to criticality. A subcritical process is one where, on average, less than one new fission reaction occurs after a single fission event. This would not lead to a self-sustaining nuclear reaction. Over time the reactions will stop on their own.

In a critical reaction, each fission process generates, on average, one additional fission event. A critical reaction is self-sustaining and will continue until all of the fissionable material is consumed. An analogy would be a line-up of dominoes. When the first domino is knocked over, it knocks over a second, which knocks over a third, and so on. This process continues until there are no more dominoes to knock over. This is shown in the video below.

In a supercritical reaction, each fission process generates, on average, more than one additional fission event. If one fission event provokes two more, those two will provoke four, which will provoke eight, and so on. A supercritical reaction grows exponentially. That means the number of fission events becomes extremely large extremely quickly.

A variable known as the effective neutron multiplication factor (which uses the symbol k) is used to represent the average number of neutrons that are generated in a fission reaction that go on to provoke new fission reactions. When k is less than one, a reaction is subcritical and will eventually die out. When k is equal to one, a reaction is critical (each fission event generates, on average, one neutron that will go on to initiate a new fission event). This is the desired situation in a nuclear reactor. When k is greater than one, a reaction is supercritical. Nuclear weapons are capable of releasing enormous amounts of energy because they are based on supercritical reactions.

If we look at a graph of the number of fission events that occur after each iteration (shown in Figure 34.5), we need to use a logarithmic scale in order to even compare critical and supercritical reactions. Assuming that one fission reaction started a chain reaction, after ten iterations, a critical reaction will have one fission event occurring; a supercritical reaction in which each iteration generates two new events (labeled k=2 in the graph) will have 512 fission events occurring; and a supercritical reaction that generates three new events with each iteration (labeled k=3 in the graph) will have nearly 20,000 fission events occurring!

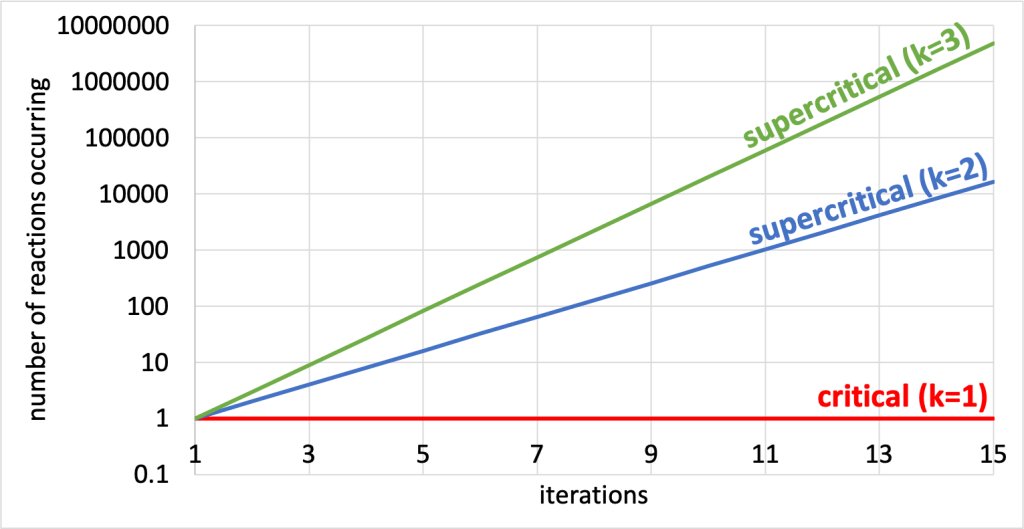
A graph depicting the number of reactions occurring (plotted logarithmically on the y-axis) vs. the number of iterations that have occurred on the x-axis. A critical reaction has only one reaction occuring regardless of the number of iterations. A supercritical k=2 reaction will start with one reaction and increase to 16384 after 15 iterations. A supercritical k=3 reaction will start with one reaction and increase to 4782969 after 15 iterations. (Because a logarithmic scale is used on the y-axes, each of these plots appears to be a straight line with different slopes.)
Figure 34.5 – A critical chain reaction will always have one reaction occurring at a time. Supercritical reactions create an exponentially increasing number of reactions over time. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Supercritical reactions are not tenable in nuclear power generation. To control the number of neutrons present in a chain reaction, control rods are used to absorb excess neutrons and keep a reaction at the critical stage. The control rod material (for example, cadmium or boron) is capable of absorbing neutrons without undergoing fission itself.

Critical mass

Because the liberated neutrons travel some average distance before initiating another fission event, there is a lower limit to how small a piece of fissionable material can be in order to maintain a chain reaction. A piece that is smaller than what is called the critical mass will allow liberated neutrons to reach the surface of the material and escape before they can trigger another fission event. (Recall the scaling effects of surface area and volume discussed earlier in this textbook: as the size of an object is scaled up, the volume grows faster than the surface area.) With a piece larger than the critical mass, the liberated neutrons will be able to initiate another fission event (due to the much greater abundance of nuclei in the volume) before they can escape to the surface.

This is the primary principle behind a nuclear fission bomb. In such a device two or more subcritical pieces (that is, pieces whose masses are less than the critical mass) are driven together using conventional explosives. When the pieces quickly come together, their combined masses form a single piece whose mass is well above the critical mass. The liberated neutrons can no longer escape to the surface of the now supercritical mass, causing the reaction to grow exponentially and resulting in a devastating explosion.

The critical mass depends on other factors such as shape and purity. The critical mass for pure uranium-235 is about 50 kg. In spherical form, this would be a ball roughly 17 cm in diameter.

Nuclear power

Natural sources of uranium consist primarily of the isotope uranium-238, which is fissionable, but not fissile. Samples of uranium ore will naturally contain some uranium-235, which is fissile. However, today less than 1% of natural uranium ore contains uranium-235. To sustain a critical chain reaction, a greater concentration of uranium-235 is required. Enrichment is a process by which the proportion of uranium-235 is increased.

Most nuclear power plants use enriched uranium (typically about 4% on average) as a fuel to create a critical chain reaction. A moderator is used to slow the neutrons released in a fission event until they travel at the right speed to cause fission in uranium-235. As mentioned earlier, control rods are used to absorb excess neutrons and prevent a super-critical reaction from occurring. Pressurized water runs through the reactor and heats up as it absorbs the energy generated by the fission reaction. In nuclear power plants in the United States, water also acts as the moderator.

The pressurized water from the reactor is sent through a heat exchanger, in which the water from the reactor transfers the heat to water in a separate line. The water in the second line boils, creating steam that spins a turbine, causing a relative rotation of a magnetic field and coil of wire. As previously discussed, this generates electricity. While the fuel is different in all turbine-powered generators, the actual mechanics of the power generation is the same for nuclear generators and fossil-fuel powered generators.

The major benefit of a nuclear reaction over fossil fuel is that there is no combustion during the actual fission process, and therefore there is no emission of greenhouse gases. In addition, uranium is a very energy dense material and per kilogram will generate much more energy than equivalent amounts of coal, oil, or gas.

Naturally, there are drawbacks to nuclear energy. While minimal, the nuclear reaction process does release small amounts of radioactivity into the environment. The uranium enrichment process can be used to create nuclear weapons. The byproducts of the fission process are themselves radioactive and have long half-lives. The safe storage of these radioactive wastes is an ongoing issue in the United States. Finally, there is always the risk of disaster in any nuclear power plant. Three Mile Island in the United States, Chernobyl in Ukraine, and Fukushima in Japan are all examples of what can happen if things go wrong. (A sidebar describing these three incidents is provided at the end of this chapter.)

Fusion

Fission is not the only way to generate energy from atomic nuclei. You may have noticed from Figure 34.2 that light elements contain a lot of mass per nucleon. If we smash hydrogen nuclei together, the result, helium, contains less mass per nucleon. This means we would generate energy in the process of binding them together. This smashing of nuclei together to form a heavier nucleus is known as nuclear fusion. All nuclei lighter than iron can release energy in the fusion process, just not with the same efficiency as the fusion of hydrogen.

Fusion is perhaps the most prevalent source of energy in our lives. That’s because the Sun generates energy using fusion, and that is where the vast majority of our energy originates! Our Sun contains a massive amount of hydrogen and converts that hydrogen to helium in the fusion process. This process is depicted in Figure 34.6. Our Sun has been generating energy in this manner for 4.6 billion years, and thankfully for us has enough fuel to keep going for about 5 billion more.

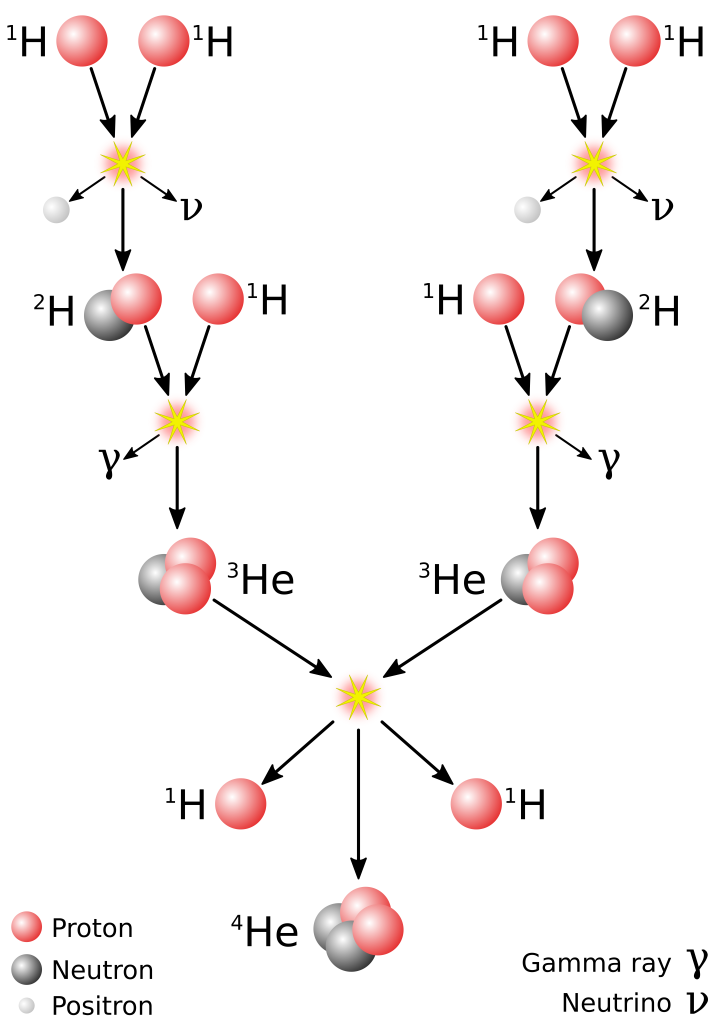
A graphic of the hydrogen fusion process in which the sun converts hydrogen into helium. At the start two hydrogen nuclei (1-H) are fused together. One nucleon converts from a proton to a neutron and emits a positron and neutrino. This generates deuterium (2-H). The dueterium nucleus fuses with another hydrogen nucleus, generating an isotope of helium (3-He) and emitting a gamma ray. Two 3-He nuclei fuse together creating one alpha particle (4-He) and two protons.
Figure 34.6 – The sun converts hydrogen into helium by fusing hydrogen nuclei together until a helium nucleus is generated. Fusion in the Sun, by Sarang, is licensed under Public Domain.

Fusion is an effective process for generating energy. Why don’t we use it on Earth? The problem is that hydrogen nuclei will experience huge amounts of electromagnetic repulsion when we try to get them to come together. To overcome this, we need to get hydrogen nuclei to come together at extraordinarily high speeds. That means extremely high temperatures (such as those found in the core of our Sun and in other stars) need to be achieved in order to get the nuclei moving fast enough.

Prior to the development of fission bombs (described earlier in this chapter), attaining the extremely high temperatures necessary to overcome the electrostatic repulsion of the hydrogen nuclei and ignite fusion was not achievable. However, the energy released in fission bombs can produce such temperatures. In 1952, the first fusion bomb was detonated in the Marshall Islands using atomic bombs as the “triggers” to detonate the fusion bomb.

While such devices demonstrate the destructive application of this knowledge, the goal of controlling fusion for use as a source of clean energy production is the other side of the coin. Harnessing the nuclear fusion of hydrogen as an energy source would be one of the pinnacles of human achievement. The fuel consists of the most abundant element in the universe (hydrogen) and the waste product is what is commonly used to fill balloons (helium). However, the quest towards achieving controlled fusion has been an arduous journey. The technological obstacles that need to be overcome are still formidable. Recent approaches focus on one of two basic schemes: magnetic confinement (in which the hot fusion plasma is held in a magnetic field in a toroidal [donut-shaped] chamber) and inertial containment (in which pellets of hydrogen fuel are bombarded by high-powered lasers from multiple directions to compress and heat the fuel) to initiate the fusion reaction.

While some recent preliminary evidence indicates that it may be possible to break even on the energy required to speed these hydrogen atoms up to the point of fusion, versus the amount of energy they produce, we are far from creating a sustained fusion reaction, let alone getting enough energy from the fusion process to use it to light up and heat our homes.

Energy in nuclear reactions

We have found that energy is released when splitting a very heavy nucleus into smaller ones (nuclear fission) and when combining very light nuclei into a heavy one (nuclear fusion). This energy comes from the conversion of mass energy according to Einstein’s famous equation,

    $$E_{released} = |\Delta m|c^2,$$

where \Delta m is the difference in mass between the initial reactants and the final products (m_{final} - m_{initial}.) Plugging in this definition of \Delta m, the equation becomes

    $$E_{released} = |(m_{final} - m_{initial})|c^2.$$

When solving this equation with numerical values, it’s helpful to use convenient units of measure (units that are neither extremely small nor extremely large). Just as we do not measure apples and baseballs in units of Earth masses, physicists generally do not measure atomic nuclei in kilograms. The kg unit is inconveniently large when discussing the mass of atomic-scale objects. For example, the mass of a proton is 1.673 \times 10^{-27}~\textrm{kg}. Similarly, the familiar energy unit, the joule, is also inconveniently large when dealing with atomic-scale objects. The mass energy of a proton is

    \begin{align*} E &= mc^2\\ &= (1.67 \times 10^{-27}~\textrm{kg})(3.00 \times 10^8~\textrm{m/s})^2\\ &= 1.51 \times 10^{-10}~\textrm{J}. \end{align*}

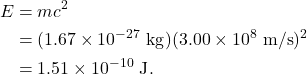
To avoid cumbersome powers of ten, more convenient units are used. For mass, we use the unified atomic mass unit (abbreviated amu or often just u). The unified atomic mass unit is defined to be 1/12 the mass of a carbon-12 atom. (For comparison, 1~\textrm{u} = 1.66054 \times 10^{-27}~\textrm{kg}.) This results in protons having a mass of 1.007276 u. The mass of a neutron is 1.008665 u.

Similarly, the energy unit generally used in atomic and nuclear physics is the electron-volt (symbol: eV), defined as the amount of energy acquired by an electron when it is accelerated through a potential difference of one volt. Nuclear energies range in the millions of eV, so the convenient unit is the MeV where 1~\textrm{MeV} = 10^6~\textrm{eV}.

1 u has a mass energy equal to 931.5 MeV. This is derived below, using the mass of 1 u in kilograms, the speed of light, and the conversion between joules and electron-volts.

    \begin{align*} E &= (1.66054 \times 10^{-27}~\textrm{kg})(2.99792 \times 10^8~\textrm{m/s})^2\\ &= 1.49241 \times 10^{-10}~\textrm{J}\\ &= \frac{1.49241 \times 10^{-10}~\textrm{J}}{1.60218 \times 10^{-19}~\textrm{J/eV}}\\ &= 9.315 \times 10^{8}~\textrm{eV}\\ &= 931.5~\textrm{MeV}. \end{align*}

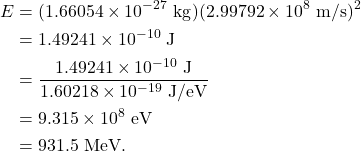
This provides a convenient conversion factor for the square of the speed of light: c^2 = 931.5~\textrm{MeV/u}.

For example, a uranium-235 nucleus can absorb a neutron to become uranium-236, which then undergoes fission. One possible outcome of the splitting is krypton-92, barium-141, and three neutrons:

    $$^{236}\textrm{U} \rightarrow ^{92}\textrm{Kr} + ^{141}\textrm{Ba} + 3\textrm{n}.$$

To calculate the energy released in this fission reaction, we must know the masses of each particle involved in the reaction. These are listed in the table below.

particle

mass

uranium-236

236.045568 u

krypton-92

91.926152 u

barium-141

140.91440 u

neutron

1.008665 u

The initial mass (m_{initial}) is 236.045568 u, which is the mass of the original nucleus. The final mass is the sum of the masses of each byproduct

    \begin{align*} m_{final} &= 91.926152~\textrm{u} + 140.91440~\textrm{u} + 3(1.008665~\textrm{u})\\ &= 235.86655~\textrm{u}. \end{align*}

Note that the final mass is less than the initial mass, resulting in a negative \Delta m value. The mass isn’t truly “missing,” but was instead converted into the energy that was released in the fission process. That released energy can be calculated as

    \begin{align*} E_{released} &= |(m_{final} - m_{initial})|c^2\\ &= |235.86655~\textrm{u} - 236.045568~\textrm{u}|(931.5~\textrm{MeV/u})\\ &= (0.179018~\textrm{u})(931.5~\textrm{MeV/u})\\ &= 166.8~\textrm{MeV}. \end{align*}

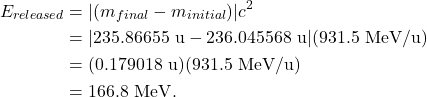
As a second example, consider the fusion reaction in which hydrogen-2 (also known as deuterium) combines with hydrogen-3 (also known as tritium) to form helium-4 and a single neutron:

    $$^2\textrm{H} + ^3\textrm{H} \rightarrow ^4\textrm{He} + \textrm{n}.$$

The mass of each particle is given in the table below.

particle

mass

hydrogen-2

2.013553 u

hydrogen-3

3.015501 u

helium-4

4.001506 u

neutron

1.008665 u

The difference in mass between the initial reactants and final products can be calculated

    \begin{align*} m_{final} - m_{initial} &= (4.001506~\textrm{u} + 1.008665~\textrm{u}) - (2.013553~\textrm{u} + 3.015501~\textrm{u})\\ &= -0.018883~\textrm{u}. \end{align*}

The energy released in this fusion reaction is

    \begin{align*} E_{released} &= |(m_{final} - m_{initial})|c^2\\ &= (0.018883~\textrm{u})(931.5~\textrm{MeV/u})\\ &= 17.6~\textrm{MeV}. \end{align*}

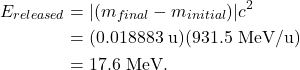
In short, to determine whether energy will be released in a nuclear reaction, compare the total mass of the initial reactants to the total mass of the final products. If m_{final} < m_{initial}, then energy is released and the reaction can occur spontaneously. Using unified atomic mass units (u) for the masses, multiply the mass difference by 931.5 MeV/u to calculate the energy released in MeV.

Binding energy

By carefully measuring the mass of any atomic nucleus (except hydrogen-1), it is found that the composite nucleus contains less mass than the sum of the masses of the individual nucleons that comprise it. In other words, the composite nucleus is less than the sum of its parts! How can this be?

The fact that protons and neutrons are bound together in the nucleus implies that energy is required to disassemble a nucleus into the individual nucleons that comprise it. The amount of energy that some external agent must supply to accomplish this task shows up as extra mass found in the individual protons and neutrons. This energy, known as the nuclear binding energy, describes the energy required to dissociate the nucleus into its constituent nucleons.

To calculate the nuclear binding energy of a particular nucleus, the mass of the nucleus as well as the number of protons and neutrons in that nucleus are required. As an example, we can calculate the binding energy of a helium-4 nucleus. Helium-4 has a mass of 4.001506 u and consists of two protons and two neutrons. The mass of two individual protons and two individual neutrons is

    \begin{align*} 2m_p + 2m_n &= 2(1.007276~\textrm{u})(1.008665~\textrm{u})\\ &= 4.031882~\textrm{u}. \end{align*}

Note that the four individual nucleons have more mass (0.030376 u more mass) than the helium-4 nucleus itself. Multiplying this mass difference by 931.5 MeV/u yields 28.30 MeV. This means that an external agent must supply 28.30 MeV of energy to dissociate the helium-4 nucleus into the two protons and two neutrons that formed it.

Of greater importance is the binding energy per nucleon. This is defined as the total nuclear binding energy divided by the total number of nucleons. The binding energy per nucleon in helium-4 is

    $$\frac{28.30~\textrm{MeV}}{4} = 7.075~\textrm{MeV}.$$

For a uranium-236 nucleus (which consists of 92 protons and 144 neutrons), a similar calculation shows that the nucleus is lighter than the 236 individual nucleons by 1.870144 u. This gives a nuclear binding energy of 1742.039 MeV. Dividing this nuclear binding energy by the 236 nucleons gives 7.382 MeV per nucleon.

The isotopes with the highest nuclear binding energy per nucleon are nickel-62 and iron-56, both of which have a value of 8.79 MeV per nucleon.

Figure 34.7 shows the average binding energy per nucleon for common isotopes plotted as a function of the number of nucleons. This is consistent with the graph shown in Figure 34.2, which shows that iron-56 has the lowest mass per nucleon. (It should be pointed out that nickel-62 has a nuclear binding energy per nucleon nearly equal to that of iron-56.) It takes more energy to dissociate an iron-56 nucleus (or a nickel-62 nucleus) into its individual nucleons than any other nucleus. This larger energy difference leads to the larger mass difference and explains why the two graphs are the same shape, just upside down.

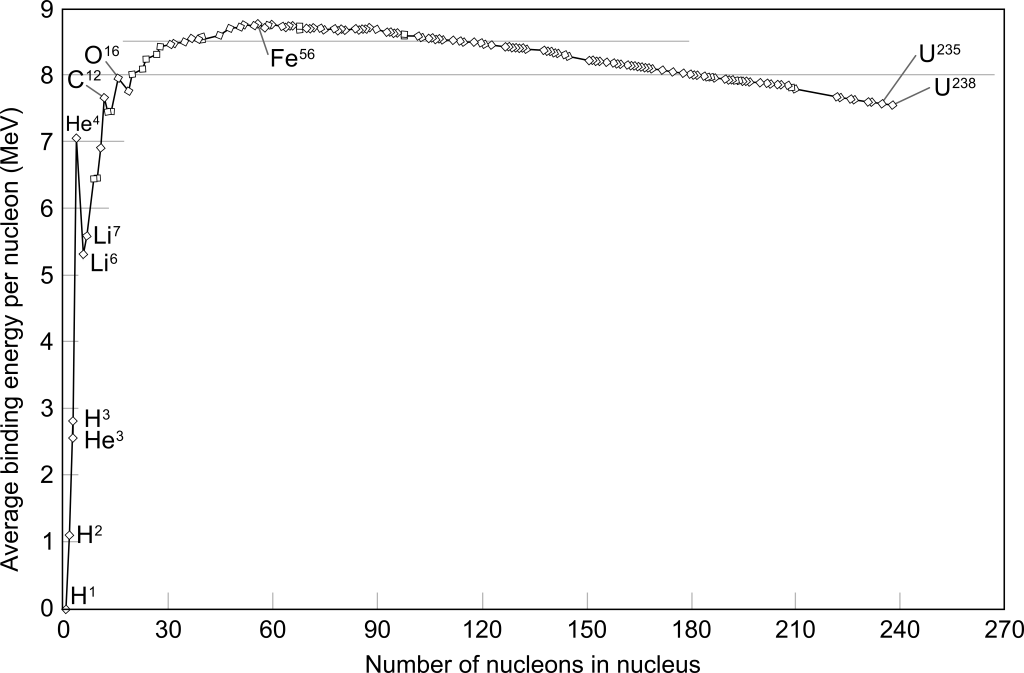
A graphic depicting the average binding energy per nucleon on the y-axis and number of nucleons on the x-axis. For the most part, the average binding energy per nucleon starts small with hydrogen-1 and increases until iron-56, then decreases slightly again through to uranium-238.
Figure 34.7 – A graph depicting the average binding energy per nucleon of common isotopes between hydrogen and uranium. Binding energy curve – common isotopes, by Fastfission, is licensed under Public Domain.

Isotopes that are lighter than iron-56 can cause a release of energy in the fusion process. Because the mass of individual nucleons is greater than the mass of these isotopes (except for hydrogen-1, which is composed of a single proton), the change in mass when binding the nucleons together into an isotope will be negative, leading to a release in energy based on E = mc^2. The fusion of isotopes with more nucleons than iron-56 will have a positive change in mass, which means that fusion of heavy elements can only occur if energy is input into the process.

On the right side of the graph, fission will cause a release of energy for isotopes that have more nucleons than iron-56 (and would require an input of energy for isotopes that have fewer nucleons than iron-56).

Stars shine by means of nuclear fusion in their cores. For relatively massive stars, the nuclear fuel is spent once the lighter nuclei have fused into iron. At that point, the star can no longer generate energy by nuclear fusion and the star collapses. The collapsing outer layers of the star bounce off the star’s dense core. This rebound results in a spectacular explosion called a supernova. It is in these explosions that the elements with atomic numbers greater than that of iron are formed. The energy of the explosion is what creates the heavy elements. All of the elements that have atomic numbers greater than those of iron and nickel were formed in the supernova explosions of previous generations of stars. These materials are then incorporated into the next generation of stars and their planetary systems. We are literally made of stardust.

Nuclear incidents

Three Mile Island

In 1979, a nuclear power station near Harrisburg, Pennsylvania, suffered a partial meltdown. The exact cause for this is complicated, as it was a series of many seemingly minor issues that led to the near-disaster.

First, an emergency water valve was left closed after maintenance had been performed on the power plant. This valve would allow water to flow into the cooling system that is part of the generator itself and that is part of the non-radioactive portion of the power plant (this water serves two purposes: it keeps the reactor cool and after heating up in this process, generates electricity by converting to steam and spinning a turbine). At the same time that this valve was closed, maintenance was being performed on the regular water lines feeding into the steam turbine. Minerals in hard water can cause plumbing to clog, and clogs of this nature were being flushed out. A clog made its way through a stuck valve and caused the water flow into the system to shut off. In an event such as this, the emergency water system should turn on to keep pressure and water flow levels normal; however, due to the valve that was closed during maintenance, this was unable to occur.

Because of the lack of cooling water reaching the reactor, pressure and temperature in the reactor portion of the power plant started to increase. This part of the plant has water in direct contact with the fuel. This water (and steam, which is also present in this type of reactor) becomes slightly radioactive. Fortunately, control rods were automatically inserted to shut down the reaction due to increases in temperature and pressure. However, a nuclear reactor does continue to generate heat even after being shut off. To cool this so-called decay heat, water is required. Because of rising pressure levels in the reactor, pressure relief valves opened to prevent a dangerous buildup of steam. Unfortunately, one of the relief valves did not close after relieving the pressure back to safe levels. To add to the issue, the indicator light did not actually indicate that the relief valve was open, so operators were unaware of this problem. This open valve caused cooling water to continue flowing out of the reactor.

Meanwhile, plant operators were concerned about keeping the correct ratio of water and steam in the reactor. Too much of either one could cause issues during normal operation of this type of power plant. Operators added some water to attempt to alleviate the issue of falling water levels, but were hesitant of accidentally adding too much. This would not have been a problem if water was not continuing to flow out of the system through the open relief valve. In addition, steam was now starting to form adjacent to the fuel itself, which was extremely dangerous as now the decay heat from the nuclear fuel could not be adequately cooled down. This caused a positive feedback loop (more steam means less cooling, which means there’s more heat, which boils more of the remaining water into steam, which means less cooling, etc.).

Fortunately, the relief valve was eventually closed, plant personnel were evacuated, and water was eventually added back to the reactor, reducing steam levels. Unfortunately, a small hydrogen explosion occurred (which, while it did not cause a lot of damage, complicated clean-up efforts) and the contaminated water and steam that had vented through the relief valve caused the relief tank to overfill, and vented into the atmosphere.

While this event could have been much worse, it remains unclear if the Three Mile Island incident caused an increase in cancer rates in the surrounding area.

Chernobyl

The Chernobyl Nuclear Power Plant, situated north of Kiev in what is now Ukraine (but at the time was part of the Soviet Union), was a power plant built in the late 1970s. The type of reactor used in this power plant is known as an RBMK reactor, which among other design flaws does not include a containment structure around the reactor. This is due to the large size of the reactor; it would take an enormously large amount of space, lots of material, and lots of money to build a suitable containment environment.

In April 1986, operators were attempting to conduct a test of a possible safety feature. The idea was to determine if, while running down the reactor, the momentum of the steam turbine would be able to power the plant’s safety features for the amount of time required to get backup diesel generators up and running. To conduct the test, the reactor needed to be powered down to a very low level (to simulate a shutdown). Operators were under a significant amount of pressure to complete the test quickly. At the same time, the test could not be conducted during the day while the day shift was operating the plant due to the fact that the power being generated from the plant was needed in the electrical system; reducing the output of the plant may have impacted the electrical needs of the surroundings. This delayed the test until closer to midnight.

The day shift initially was able to reduce power to about half of normal output. At the same time, they also shut down emergency cooling systems. While turning off the emergency cooling system had no direct effect on what was to come later, it was a sign of the lax safety culture in existence in the power plant to turn off (and keep off) an emergency backup system.

When the plant operators were finally allowed to reduce power, power levels were reduced to lower levels than anticipated. This caused an issue known as “xenon poisoning” where lots of xenon-135, a byproduct of the fission process, is generated. Because the power levels were low, this xenon-135 wasn’t being bombarded by as many neutrons to convert it to xenon-136. Xenon-135 is a great absorber of neutrons (xenon-136 is not), and acts to slow the reaction further. Because xenon-135 has a relatively long half-life, it takes a long time for the effects of xenon poisoning to stop. (If the fission reaction is occurring at high enough levels, the abundance of neutrons converts the xenon-135 to xenon-136, causing this to be a non-issue.) Operators removed many of the control rods in the reactor to make up for this xenon poisoning and to keep the reaction critical.

Meanwhile, a lot of cooling water was flowing into the reactor, more so than was needed for the lower power output of the plant. This caused low levels of steam and pressure in the reactor, and also acted as a further neutron absorber (water is a good absorber of neutrons). More control rods were removed to keep the reaction critical as a response to the excess water levels. Some of the cooling water was being pumped in by pumps connected to the steam generator as part of the safety test. (The question was: if the reactor shuts down, will the momentum of the steam generator produce enough power to keep cooling water flowing before the diesel backups start powering the pumps?)

When the test finally started, the valve to release steam into the turbine and generator was closed. This caused steam pressure to build up in the reactor (if it could not go into the turbine, it instead would stay in the reactor area). Meanwhile, the cooling water pumps powered by the generator (which was no longer producing much, if any, power, as expected) stopped flowing. This caused an increase in temperatures, causing much of the cooling water in the reactor to convert to steam. Steam does not absorb neutrons as well as liquid water does due to its low density.

At this point, with most of the control rods having been removed, and water converting to steam, there was now an increase in neutrons and the reaction levels increased. This generated more heat and steam, which led to more neutrons and a higher reaction level. This process continued in a positive feedback loop.

An emergency shutdown button was activated, which caused control rods to be inserted back into the reactor. Unfortunately, the design of the RBMK reactor control rods contained a huge flaw: the ends of the control rods that would move first into the reactor as they were lowered down were graphite, a moderator. Instead of slowing down the reaction, this caused an increase in the reaction!

Eventually, the pressure in the reactor became so great that there was a steam explosion. Because there was no containment structure, radioactive debris and fuel were ejected all around the plant. This caused many fires and severed coolant lines. (Although at this point cooling water would not have stopped the damage.) The fire spread radioactive particles throughout not only the plant, but also throughout the USSR and Europe. Many plant operators, firefighters, and rescue workers were killed either directly by the explosion, or later by their exposure to extreme levels of radioactive nuclei.

A steel and concrete structure known as a “sarcophagus” was built to reduce the spread of further contamination, but about 2,600 km2 of the surrounding area has been declared an “exclusion zone” to prevent human inhabitants from residing in an extremely radioactive environment.

Fukushima

The Fukushima nuclear accident occurred on March 11, 2011 as a result of the Great East Japan Earthquake. While the earthquake and subsequent tsunami caused significant damage to the nuclear power plant, the design of the plant itself contributed greatly to the severity of the accident.

The Fukushima Daiichi Nuclear Power Plant (the first of two nuclear power plants in Fukushima) was built along the coastline of Japan. The proximity to the Pacific Ocean ensured that the reactor would have access to lots of cooling water. When construction began in the late 1960s, a cliff that was originally present on the coastline at the site was removed. This allowed the power plant to be more easily anchored to bedrock (an important consideration in an earthquake-prone area), and also enabled easier pumping of cooling ocean water into the plant. (If the plant had been built on top of a cliff, pumps would have to overcome gravity to pump the water significantly above sea level. This would essentially make the power plant less efficient, as some of the power generated by the plant would be spent pumping water instead of going directly to the power grid.)

Backup diesel generators (used in case of a power outage to keep backup and safety systems online) were installed in the lowest level of the plant. This may have been an OK decision for locations significantly above sea level, but was a very problematic decision in the construction of the Fukushima Daiichi plant.

In general, the power plant was designed to withstand probable, predictable geological events, not a worst-case scenario. There is always a tradeoff between extremely safe design (designing for a worst-case scenario) and keeping a design cost- and power-efficient (designing for probable scenarios). Unfortunately, the design of this reactor would contribute to its downfall.

On March 11, 2011 the Great East Japan Earthquake registered at a 9.0 on the Richter scale. This earthquake knocked out power to the reactor. Thankfully, the diesel backup generators came online to power safety systems. All of the reactors at the plant were automatically shut down. However, fission reactors do continue to produce heat (known as decay heat because it is generated by byproducts of radioactive decay) even after the fusion reaction is shut down.

A few minutes after the earthquake hit the coast, a 13-meter-tall tsunami hit the power plant. The plant had been modified at that point to withstand 5.7 meters, which was insufficient to protect from the effect of the gigantic waves from the tsunami. The plant was flooded, cooling lines were severed, and the diesel generators were flooded out. Now all of the safety systems went offline. Fresh cooling water could not be pumped into the reactors, and the cooling water that was already in the reactors could not be pumped out after heating up. The core temperatures of many units became so high that the fuel melted through the containment structures (this is known as a meltdown). In addition, hydrogen gases built up and caused explosions.

Radioactive byproducts were released into the surrounding areas, and many thousands of people living near the power plant were evacuated. More recently (2023), there has been public outcry over the release of radioactive cooling water back into the Pacific Ocean.

Further reading

Further reading

  • United States Nuclear Regulatory Commission – The US NRC is tasked with regulating the safety of nuclear power plants in the United States. Their website contains a lot of information about nuclear power and related issues.
  • What are Small Modular Reactors (SMRs) – This website explains the physics behind small modular reactors, which can produce a lot of energy in a relatively small size.
  • Advanced reactor systems – This website explains some new nuclear reactor technologies (known as Gen 4) that may be able to fuel our power needs into the next few decades.

Practice questions

Conceptual comprehension

  1. In a commercial nuclear fission reactor that generates electricity, what value for the neutron multiplication number, k, is most desirable? Why?
  2. A uranium-235 nucleus absorbs a neutron to become uranium-236. One possible outcome of the resulting fission reaction is cesium-137, rubidium-97, and some number of individual neutrons. How many neutrons would be generated in this reaction?
  3. If instead the uranium-236 in the previous question fissions into tellurium-137, an isotope of zirconium, and two neutrons, what is the atomic mass number of the zirconium isotope involved in this reaction?
  4. How is it possible that energy can be released by splitting heavy nuclei into lighter ones and by fusing light nuclei into heavier ones?

Numerical analysis

  1. Consider a supercritical chain reaction in which each fission event induces two successive events. (That is, the neutron multiplication number, k, is equal to two.) How many fission events will take place during the 6th cycle? After the 6th cycle, how many total fissions will have taken place since the start of the reaction?
  2. In a critical fission reaction (k=1), each fission event goes on to initiate only one successive event. If each successive event takes place with an average time interval of 10 nanoseconds, how long will it take for 1023 fission events to occur?
  3. If instead, the reaction described in the previous questions was supercritical with a neutron multiplication number k=2, how long would it take for 1023 fission events to occur? How many times faster is this reaction compared to the critical reaction? (Hint: First determine how many cycles occur for a total of 1023 fission events.)
  4. The power output of the Sun is 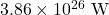3.86 \times 10^{26}~\textrm{W}. Calculate the rate at which the sun is converting mass into energy. Give your answer in kg/s. (Hint: Recall that 1 W = 1 J/s.  Then use Einstein’s famous equation.)
  5. How much energy is released when a plutonium-244 nucleus alpha decays into neptunium-240? The required masses are given in the table below.

particle

mass

plutonium-244

244.064204 u

neptunium-240

240.056162 u

helium-4

4.001506 u
  1. Consider the following fission reaction: 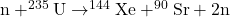\textrm{n} + ^{235}\textrm{U} \rightarrow ^{144}\textrm{Xe} + ^{90}\textrm{Sr} + 2\textrm{n}. How much energy is released in this reaction? The required masses are given in the table below.

particle

mass

neutron

1.008665 u

uranium-235

235.043930 u

xenon-144

143.93851 u

strontium-90

89.907738 u
  1. Consider the nuclear reactions listed below. How much energy is released in each reaction? The mass of helium-3 is 3.016029 u. Refer to earlier tables for the masses of the other particles.
    1. ^2\textrm{H} + ^2\textrm{H} \rightarrow ^3\textrm{H} + ^1\textrm{H}
    2. ^3\textrm{He} + ^3\textrm{He} \rightarrow ^4\textrm{He} + ^1\textrm{H} + ^1\textrm{H}
  2. Calculate how much energy is needed to disassemble a nickel-62 nucleus into its individual protons and neutrons.
  3. Calculate the average mass per nucleon of a carbon-12 nucleus.
  4. Calculate the energy required to dissociate 12 micrograms of carbon-12 into individual protons and neutrons. If the burning of one gallon of gasoline releases 140 MJ of energy, calculate how many gallons of gasoline are potentially needed to dissociate those 12 micrograms of carbon-12 atoms.

Hands-on experiments

  1. If you have a set of dominoes, carefully arrange them so that one domino will knock over a second, which will knock over a third, and so on. This will represent a critical chain reaction. If you have a stopwatch, knock over the first domino while pressing the start button on your stopwatch. Stop the stopwatch when the last domino falls. How long did the reaction take? Divide by the number of dominoes minus one (the first knock that you initiated) to determine how long it took for each individual reaction event to occur. If you can, try setting up the dominoes such that one will knock over two, and each of those dominoes knock over two more. This represents a supercritical (k=2) chain reaction. How long did that reaction take to knock over the same number of dominoes? Did you encounter any difficulties in setting up the supercritical reaction?
definition

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Conceptual Physics Copyright © 2024 by Alyssa J. Pasquale, Ph.D.; David R. Fazzini, Ph.D.; and Carley Bennett, Ph.D. is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book